Droga w fizyce
Droga jest wielkością fizyczną, która opisuje długość trasy pokonanej przez ciało w czasie jego ruchu. W przypadku ruchu prostoliniowego rozróżniamy kilka podstawowych typów ruchów, w których możemy precyzyjnie wyznaczyć drogę.
1. Ruch Prostoliniowy Jednostajny
W ruchu jednostajnym prostoliniowym ciało porusza się z stałą prędkością, co oznacza, że prędkość nie zmienia się w czasie. Droga \(s\) w tym przypadku jest opisana wzorem:
gdzie:
- \( v \) – stała prędkość ciała,
- \( t \) – czas ruchu.
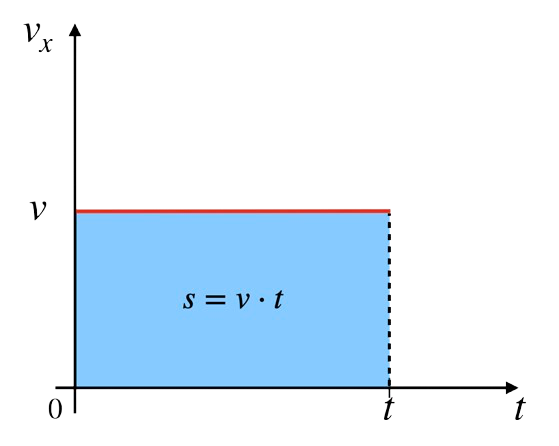
Wyprowadzenie wzoru dla drogi w ruchu jednostajnym prostoliniowym polega na wykorzystaniu wykresu \(v(t)\), gdzie prędkość \(v\) jest stała. Droga \(s\) to pole prostokąta pod wykresem:
2. Ruch Prostoliniowy Jednostajnie Przyspieszony
W ruchu prostoliniowym jednostajnie przyspieszonym prędkość ciała rośnie liniowo w czasie z przyspieszeniem \( a \). Droga przebyta przez ciało wyraża się wzorem:
gdzie:
- \( v_0 \) – początkowa prędkość ciała,
- \( a \) – przyspieszenie,
- \( t \) – czas ruchu.
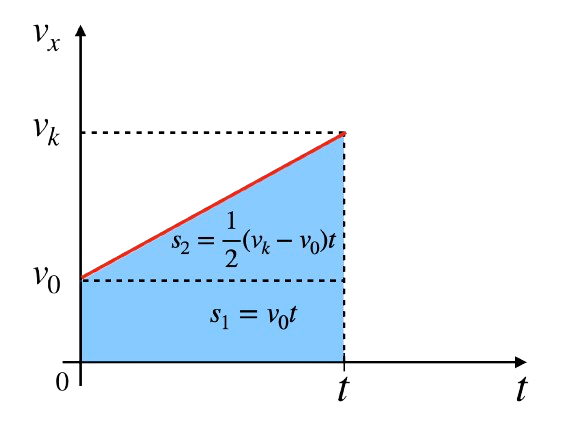
Wyprowadzenie wzoru w ruchu jednostajnie przyspieszonym polega na wykorzystaniu wykresu \(v(t)\), który jest linią prostą. Droga jest równa polu trójkąta i prostokąta:
Za \(v_k-v_0\) możemy podstawić \(\Delta v \) i wykorzystać wzór na przyśpieszenie: \(a= \frac{\Delta v}{t}\), aby otrzymać ostateczny wzór:
3. Ruch Prostoliniowy Jednostajnie Opóźniony
W ruchu prostoliniowym jednostajnie opóźnionym prędkość ciała maleje liniowo w czasie, a przyspieszenie \( a \) jest skierowane przeciwnie do ruchu. Droga \( s \) jest wówczas opisana wzorem:
gdzie:
- \( v_0 \) – początkowa prędkość ciała,
- \( a \) – opóźnienie (wartość przyspieszenia skierowanego przeciwnie do ruchu),
- \( t \) – czas ruchu.
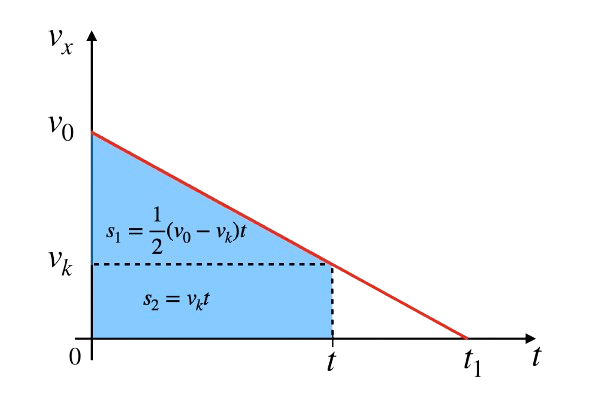
Wyprowadzenie wzoru w ruchu jednostajnie opóźnionym polega na wykorzystaniu wykresu \(v(t)\), który również jest linią prostą, ale tym razem nachyloną odwrotnie - prędkość zmniejsza się do wartości \(0\). Droga przebyta przez ciało jest sumą pól trójkąta i prostokąta na wykresie:
Możemy to zapisać jako:
Za \(v_k\) możemy podstawić \(v + \Delta v\):
Wykorzystujemy wzór na przyśpieszenie: \(a= \frac{\Delta v}{t}\), aby otrzymać ostateczny wzór (pamiętamy że \(\Delta v\) w tym przypadku będziee ujemna ponieważ \(v_k-v_0 < 0\)), więc za przyśpieszenie musimy podstawić ujemną wartość przyśpieszenia!:
Obliczanie Drogi jako Pole Figury
W fizyce droga przebyta przez ciało w dowolnym ruchu prostoliniowym może być obliczona jako pole figury pod wykresem prędkości \( v(t) \) względem czasu \( t \). Oznacza to, że znajomość wykresu prędkości umożliwia obliczenie przebytej drogi za pomocą geometrycznych metod:
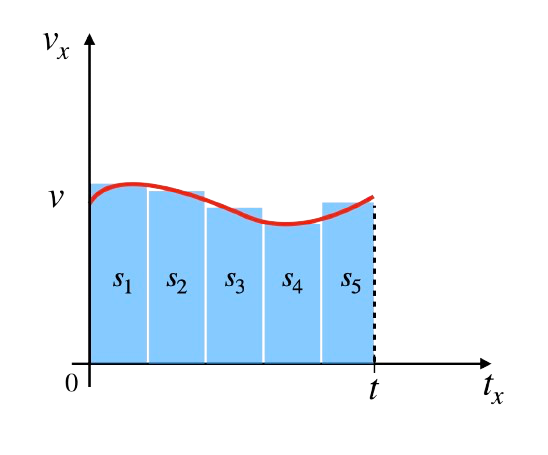
Równanie to opisuje sumowanie prędkości w czasie jako całkowitą drogę, którą ciało przebyło.
5. Zadanie: Obliczanie Drogi Przebytej przez Ciało
Zadanie: Ciało rozpędza się przez 8 sekund, osiągając prędkość 20 m/s, następnie porusza się ruchem jednostajnym przez 12 sekund, a potem hamuje przez 5 sekund, aż do zatrzymania. Oblicz całkowitą drogę przebytą przez ciało.
Rozwiązanie (Metoda 1 - Obliczenia):
Krok 1: Obliczamy drogę \( s_1 \), którą ciało przebyło podczas rozpędzania. Przyspieszenie jest stałe: \[ a = \frac{v}{t} = \frac{20 \, \text{m/s}}{8 \, \text{s}} = 2.5 \, \text{m/s}^2 \] Droga \( s_1 \) jest opisana wzorem: \[ s_1 = \frac{1}{2} a t^2 = \frac{1}{2} \cdot 2.5 \, \text{m/s}^2 \cdot (8 \, \text{s})^2 = 80 \, \text{m} \]
Krok 2: Obliczamy drogę \( s_2 \), którą ciało przebyło podczas ruchu jednostajnego: \[ s_2 = v \cdot t = 20 \, \text{m/s} \cdot 12 \, \text{s} = 240 \, \text{m} \]
Krok 3: Obliczamy drogę \( s_3 \), którą ciało przebyło podczas hamowania. Przyspieszenie (opóźnienie) to: \[ a = \frac{-v}{t} = \frac{-20 \, \text{m/s}}{5 \, \text{s}} = -4 \, \text{m/s}^2 \] Droga \( s_3 \) jest opisana wzorem: \[ s_3 = \frac{1}{2} v t = \frac{1}{2} \cdot 20 \, \text{m/s} \cdot 5 \, \text{s} = 50 \, \text{m} \]
Krok 4: Sumujemy wszystkie drogi: \[ s = s_1 + s_2 + s_3 = 80 \, \text{m} + 240 \, \text{m} + 50 \, \text{m} = 370 \, \text{m} \]
Odpowiedź:
Całkowita droga przebyta przez ciało wynosi \( 370 \, \text{m} \).
Rozwiązanie (Metoda 2 - Wykres):
Krok 1: Rysujemy wykres prędkości \( v(t) \):
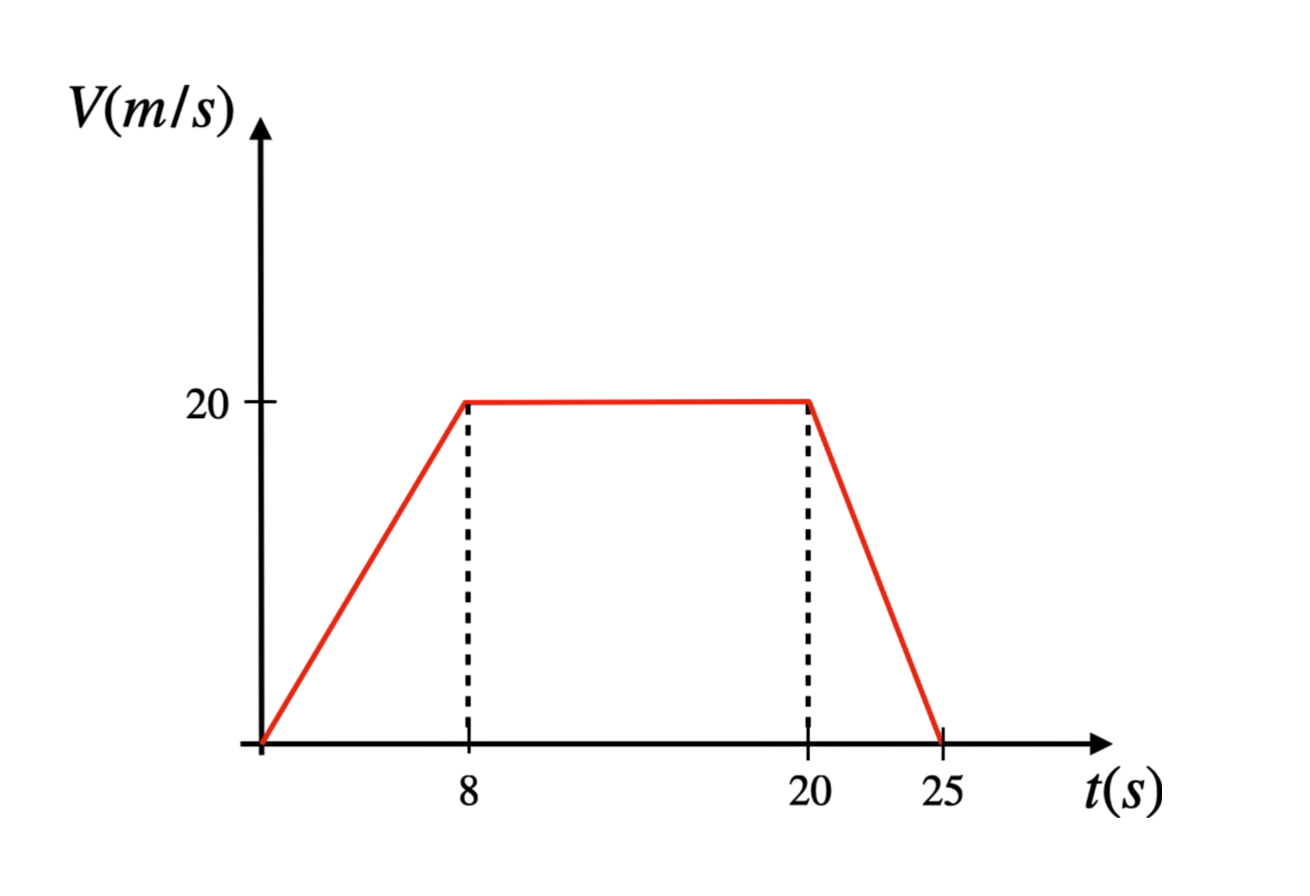
Krok 2: Obliczamy drogę jako pole pod wykresem:
- Trójkąt (przyspieszanie): \( \frac{1}{2} \cdot 20 \, \text{m/s} \cdot 8 \, \text{s} = 80 \, \text{m} \)
- Prostokąt (ruch jednostajny): \( 20 \, \text{m/s} \cdot 12 \, \text{s} = 240 \, \text{m} \)
- Trójkąt (hamowanie): \( \frac{1}{2} \cdot 20 \, \text{m/s} \cdot 5 \, \text{s} = 50 \, \text{m} \)
Odpowiedź:
Całkowita droga przebyta przez ciało wynosi \( 370 \, \text{m} \).