Droga
\(S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\ = \frac{v_0 \cdot t + v_k \cdot t}{2} \)
\(S\) - Droga
\(v_0\) - Początkowa Prędkość
\(v_k\) - Końcowa Prędkość
\(t\) - Czas
\(a\) - Przyspieszenie
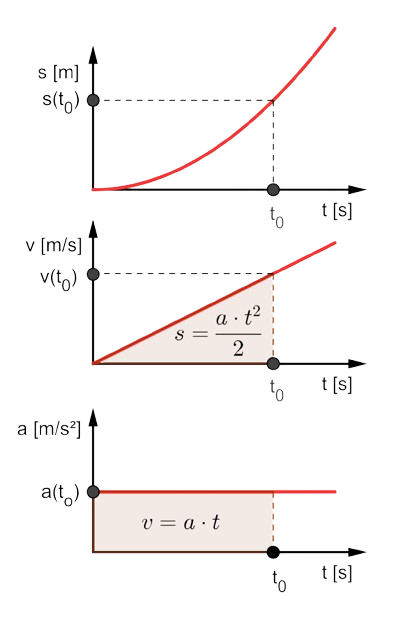
Źródło: MikeRun
Droga w ruchu jednostajnie zmiennym to odległość pokonana przez ciało poruszające się z przy stałym przyspieszeniu lub opóźnieniu.
Przykład z życia:
Kiedy samochód jednostajnie przyspiesza lub hamuje na autostradzie. Jeśli samochód przyspiesza z 30 m/s do 60 m/s w ciągu 10 sekund, to jego droga w tym czasie będzie większa niż w pierwszych 10 sekundach, kiedy jechał z 10 m/s do 30 m/s.
Samochód porusza się z przyspieszeniem 2 m/s² przez 6 sekund. Jaką odległość przejedzie w tym czasie, jeśli miał początkową prędkość 36 km/h?
Odpowiedź:
\(s \approx 96 \, \text{m} \)