\(v = \sqrt{\frac{2 \cdot g \cdot (h_p - h_k)}{1 + \frac{I}{mR^2}}}\)

\(v\) - Prędkość Liniowa

\(g\) - Przyspieszenie Ziemskie

\(h_p\) - Wysokość Początkowa

\(h_k\) - Wysokość Końcowa

\(I\) - Moment Bezwładności

\(m\) - Masa

\(R\) - Promień

*We wszytskich obliczeń zakładamy że bryła porusza się bez poślizgu.

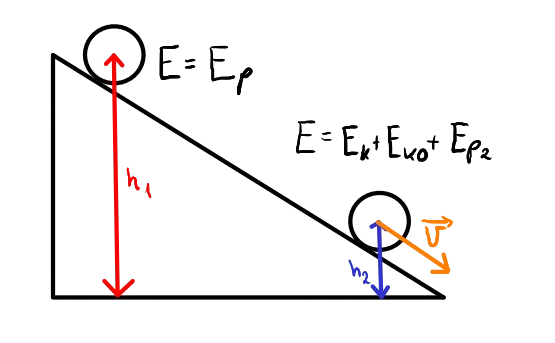
Gdzie:

• \(E\) - Energia całkowita ciała
• \(E_p\) - Energia potencjalna ciała
• \(E_k\) - Energia kinteyczna ciała
• \(E_ko\) - Energia kinteyczna obrotowa ciała

Korzystamy z zasady zachowania energii. Energia początkowa ciała będzie równała się końcowej energii ciała. Na początku ciało spoczywa, więc posiada tylko energię potencjalną, z czasem jednak energia potencjalna stopniowo zmienia się na kinetyczną oraz energię kinetyczną obrotową.

Wzór na energię potencjalną: \( m \cdot g \cdot h \)

Wzór na energię kinetyczną: \( \frac{m \cdot v^2}{2} \)

Wzór na energię kinetyczną obrotową: \( \frac{I \cdot \omega^2}{2} \)

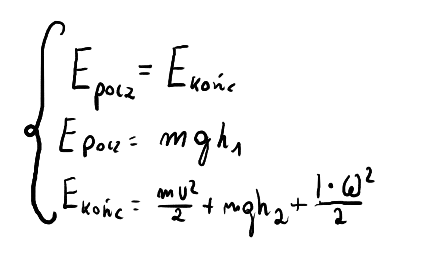
Gdzie:

• \( E_{\text{pocz}} \) - Energia początkowa ciała
• \( E_{\text{końc}} \) - Energia końcowa ciała