Przyspieszenie Układu Ciał
\(\vec{a} = \frac{\sum \vec{F} - \sum T}{\sum m}\)
\(\vec{a}\) - Przyspieszenie
\(\vec{F}\) - Siła
\(T\) - Siła tarcia
\(m\) - Masa
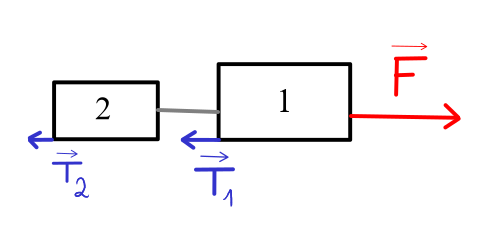
Układ ciał poruszających się po płaszczyźnie poziomej. Zakładamy że ciała są połączone nieważkimi linkami (w celu ułatwiania obliczeń). Poniższe zdjęcie ilustruje przykładową sytuację, którą opisuje wzór na przyspieszenie układu ciał.
Przykładem z życia codziennego, który ilustruje przyspieszenie układu ciał, może być sytuacja ciągnięcia skrzyń połączonych linkami. Jeśli ciągniemy skrzynie, musimy przyłożyć siłę, aby je przyspieszyć, a siła ta zależy od masy skrzyń oraz od sił tarcia generowanych przez szorstkie podłoże.