Spis treści

1. Wstęp
2. Łączenie Szeregowe
3. Łączenie Równoległe
4. Przykład Zadania
5. Upraszczanie Obwodu

Łączenie Oporników

Łączenie oporników (rezystorów) jest podstawowym zagadnieniem w elektronice, które pozwala na regulację oporu całkowitego obwodu. Wyróżniamy dwa główne typy łączenia: szeregowe oraz równoległe.

1. Wstęp

Rezystory są elementami elektronicznymi, które ograniczają przepływ prądu. Łączenie oporników pozwala na uzyskanie różnych wartości oporu zastępczego \( R_z \), co jest niezbędne w projektowaniu obwodów. Poniżej omówimy dwa podstawowe sposoby łączenia: szeregowe i równoległe, ich właściwości oraz zastosowania.

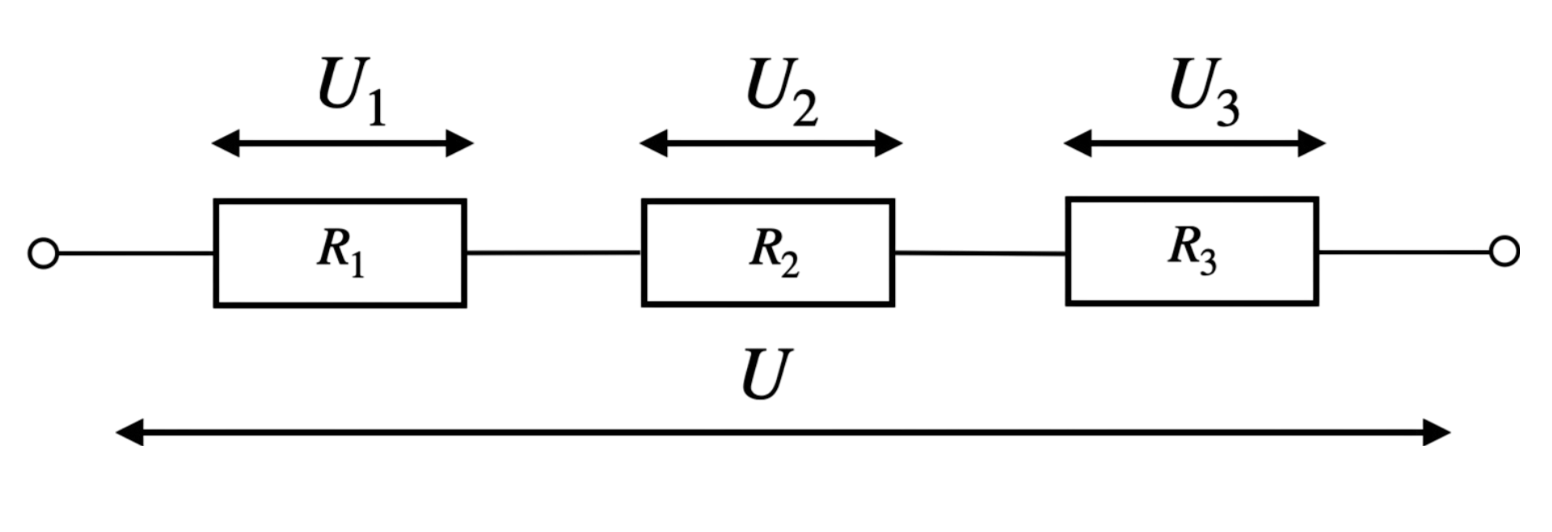
2. Łączenie Szeregowe

W łączeniu szeregowym oporniki są połączone jeden za drugim, a prąd przepływa przez każdy z nich kolejno. Całkowity opór zastępczy \( R_z \) w takim połączeniu jest sumą wartości poszczególnych oporników:

Schemat połączenia szeregowego oporników

\( R_z = R_1 + R_2 + R_3 + \ldots \)

Pokaż wyprowadzenie wzoru

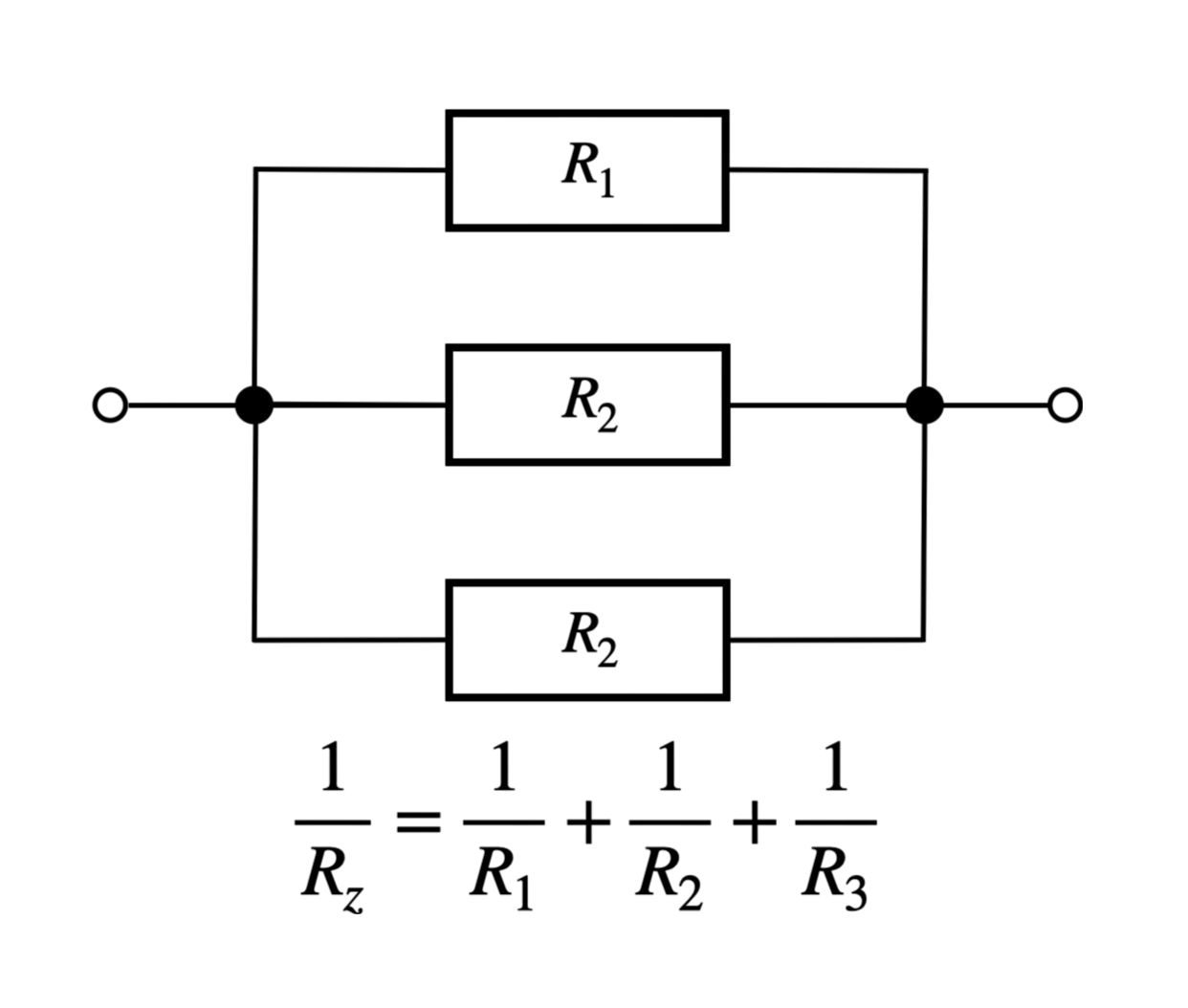
3. Łączenie Równoległe

W łączeniu równoległym wszystkie oporniki są połączone do tych samych zacisków, dzieląc prąd pomiędzy siebie. Odwrotność oporu zastępczego \( R_z \) jest sumą odwrotności oporów poszczególnych rezystorów:

Schemat połączenia równoległego oporników

\( \frac{1}{R_z} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \ldots \)

Pokaż wyprowadzenie wzoru

4. Przykład Zadania: Obliczanie Oporu Zastępczego

Przykład: W obwodzie znajdują się trzy oporniki: \( R_1 = 10 \, \Omega \), \( R_2 = 20 \, \Omega \) oraz \( R_3 = 30 \, \Omega \). \( R_1 \) jest połączony szeregowo z równoległym połączeniem \( R_2 \) i \( R_3 \). Oblicz opór zastępczy \( R_z \) obwodu.

Pokaż rozwiązanie krok po kroku

Rozwiązanie:

Krok 1: Obliczamy opór zastępczy dla połączenia równoległego \( R_2 \) i \( R_3 \):

\( \frac{1}{R_{2,3}} = \frac{1}{R_2} + \frac{1}{R_3} = \frac{1}{20} + \frac{1}{30} \)

\( R_{2,3} = \frac{1}{\frac{1}{20} + \frac{1}{30}} = 12 \, \Omega \)

Krok 2: Dodajemy opór \( R_1 \), który jest połączony szeregowo:

\( R_z = R_1 + R_{2,3} = 10 + 12 = 22 \, \Omega \)

Odpowiedź: Opór zastępczy obwodu wynosi \( R_z = 22 \, \Omega \).

5. Przykład Zadania: Obliczanie Oporu Zastępczego

Zadanie: Uprość poniższy układ oporników i oblicz opór zastępczy tego obwodu. Załóż że wszytskie oporniki, mają taki sam opór:

Pokaż rozwiązanie krok po kroku

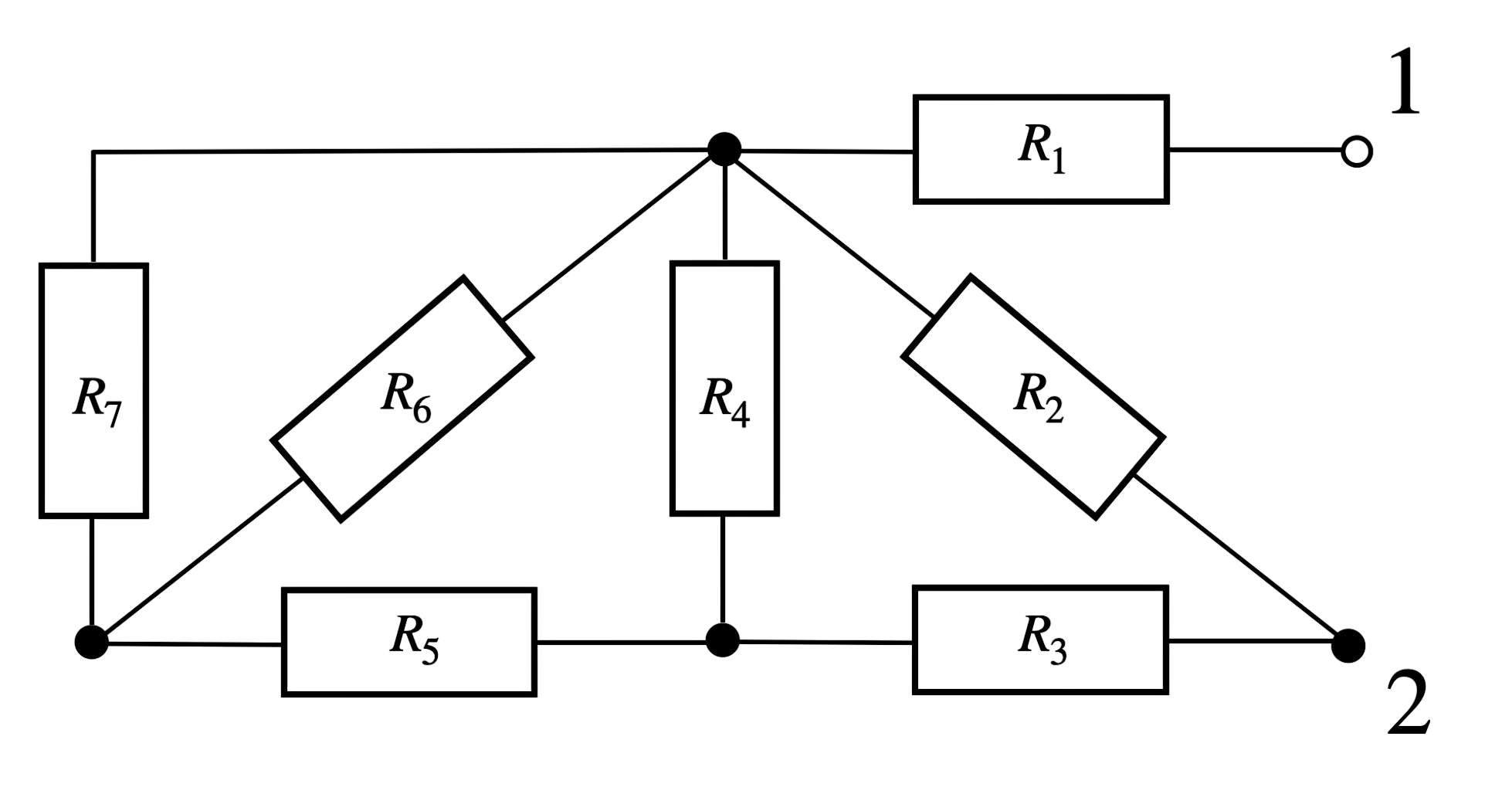
Rozwiązanie:

Krok 1: Zacznijmy od przerysowania układu, w bardziej czytelny sposób:

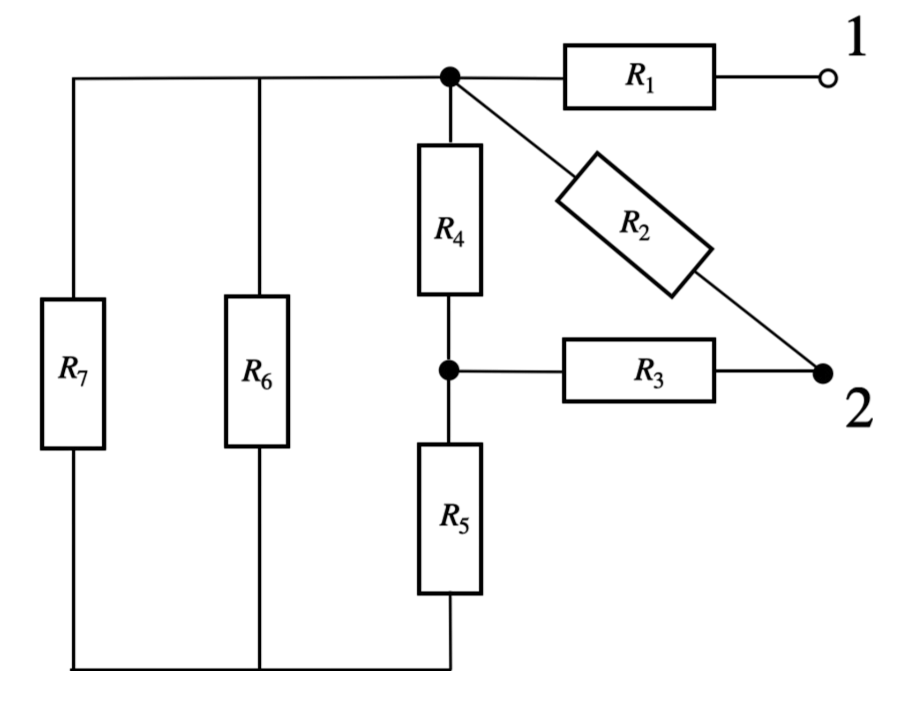
Krok 2: Zastępujemy oporniki \( R_7 \) i \( R_6 \), jednym (którego wartość oporu zastępczego będzie wynosić \(\frac{1}{2} R_6\), ponieważ \( R_7 \) i \( R_6 \) są połączone równolegle). Otrzymujemy:

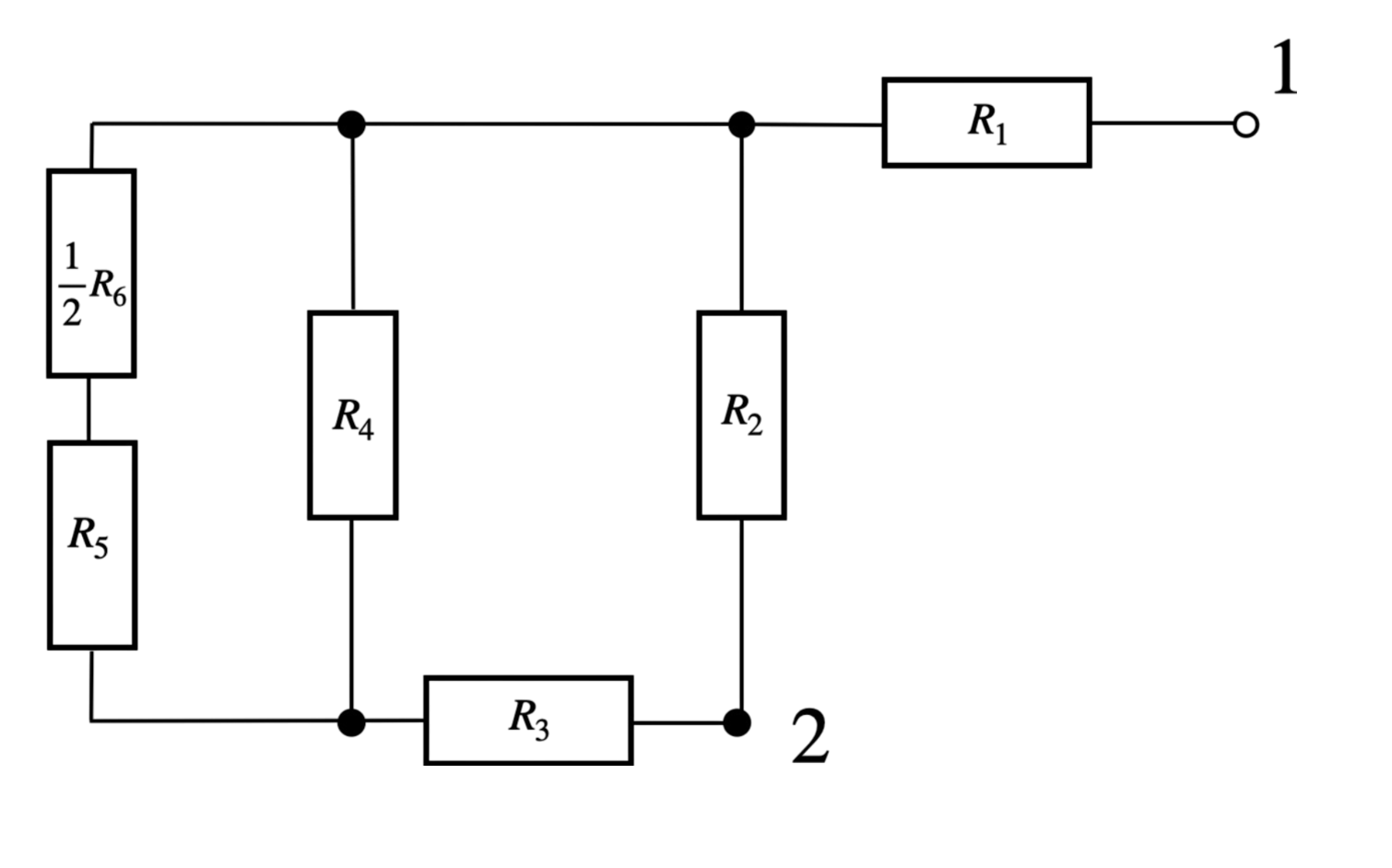
Krok 3: Przerysowujemy układ w sposób bardziej przejrzysty:

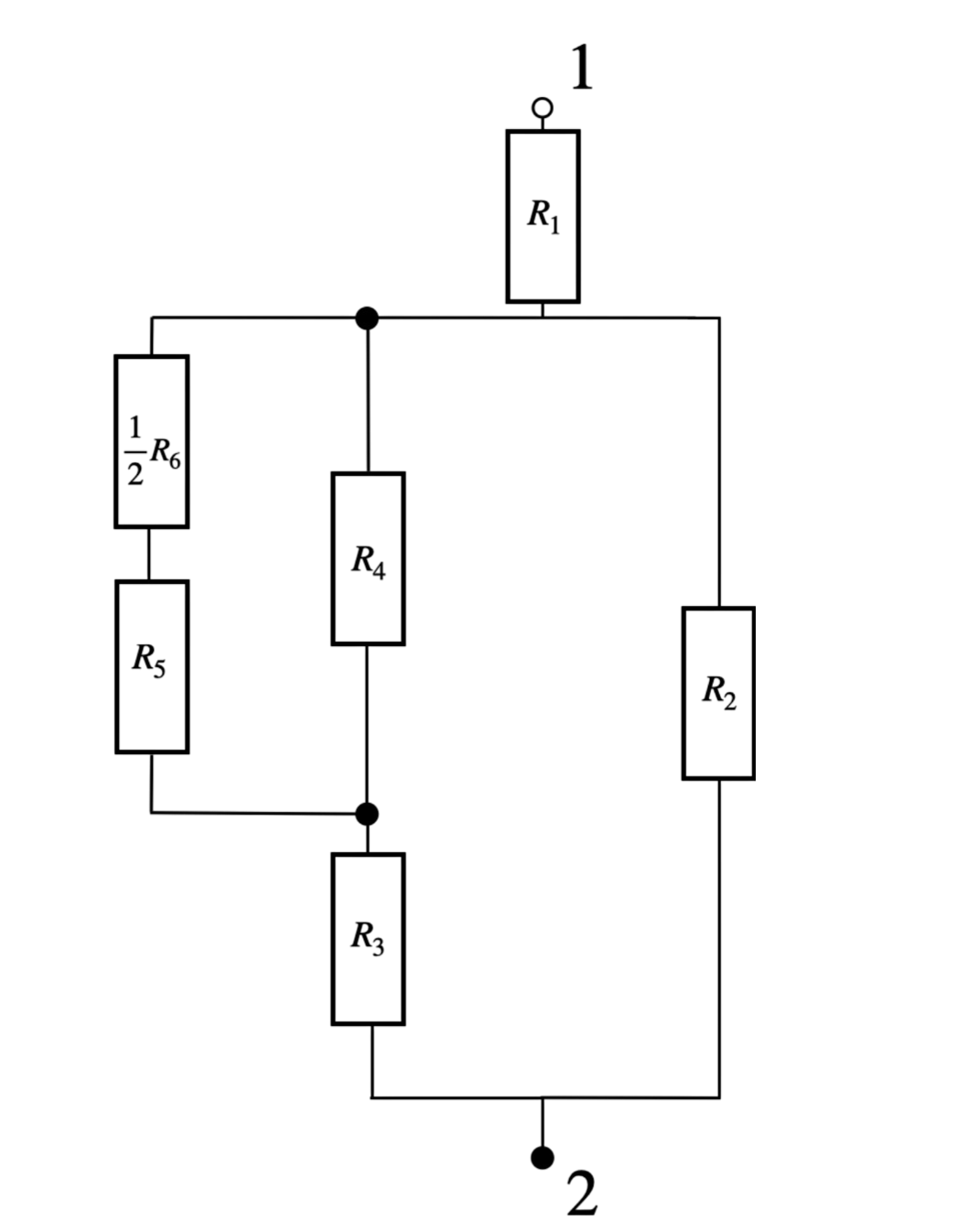
Krok 4: Zastępujemy oporniki \( R_5 \) i \(\frac{1}{2} R_6 \), jednym (którego wartość oporu zastępczego będzie wynosić \(\frac{3}{2} R_6\), ponieważ są połączone szeregowo). Otrzymujemy:

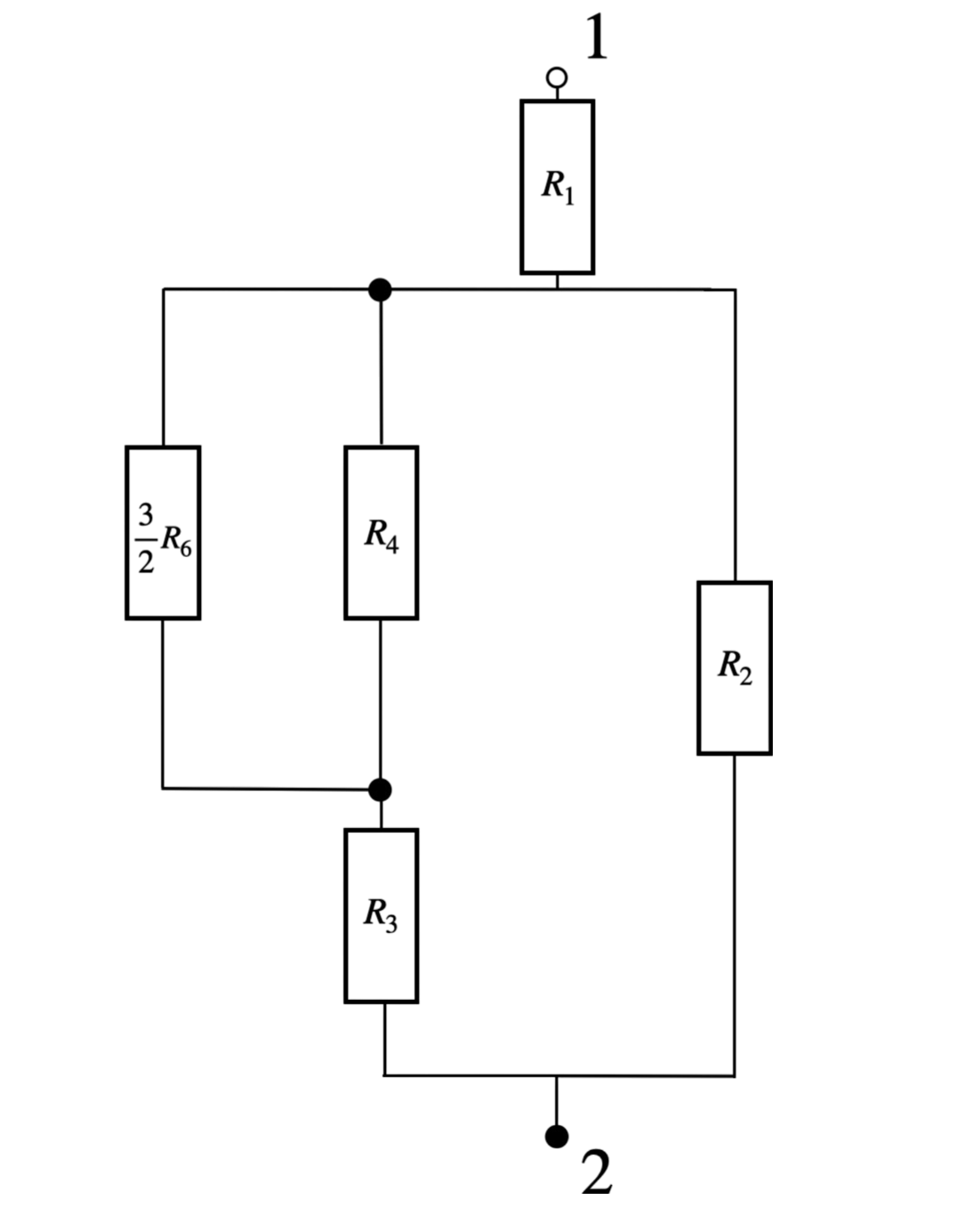
Krok 5: Zastępujemy oporniki \( R_4 \) i \(\frac{3}{2} R_6 \), jednym (którego wartość oporu zastępczego będzie wynosić \(\frac{3}{5} R_6\), ponieważ są połączone równolegle). Otrzymujemy:

Krok 6: Zastępujemy oporniki \( R_3 \) i \(\frac{3}{5} R_6 \), jednym (którego wartość oporu zastępczego będzie wynosić \(\frac{8}{5} R_6\), ponieważ są połączone szeregowo). Otrzymujemy:

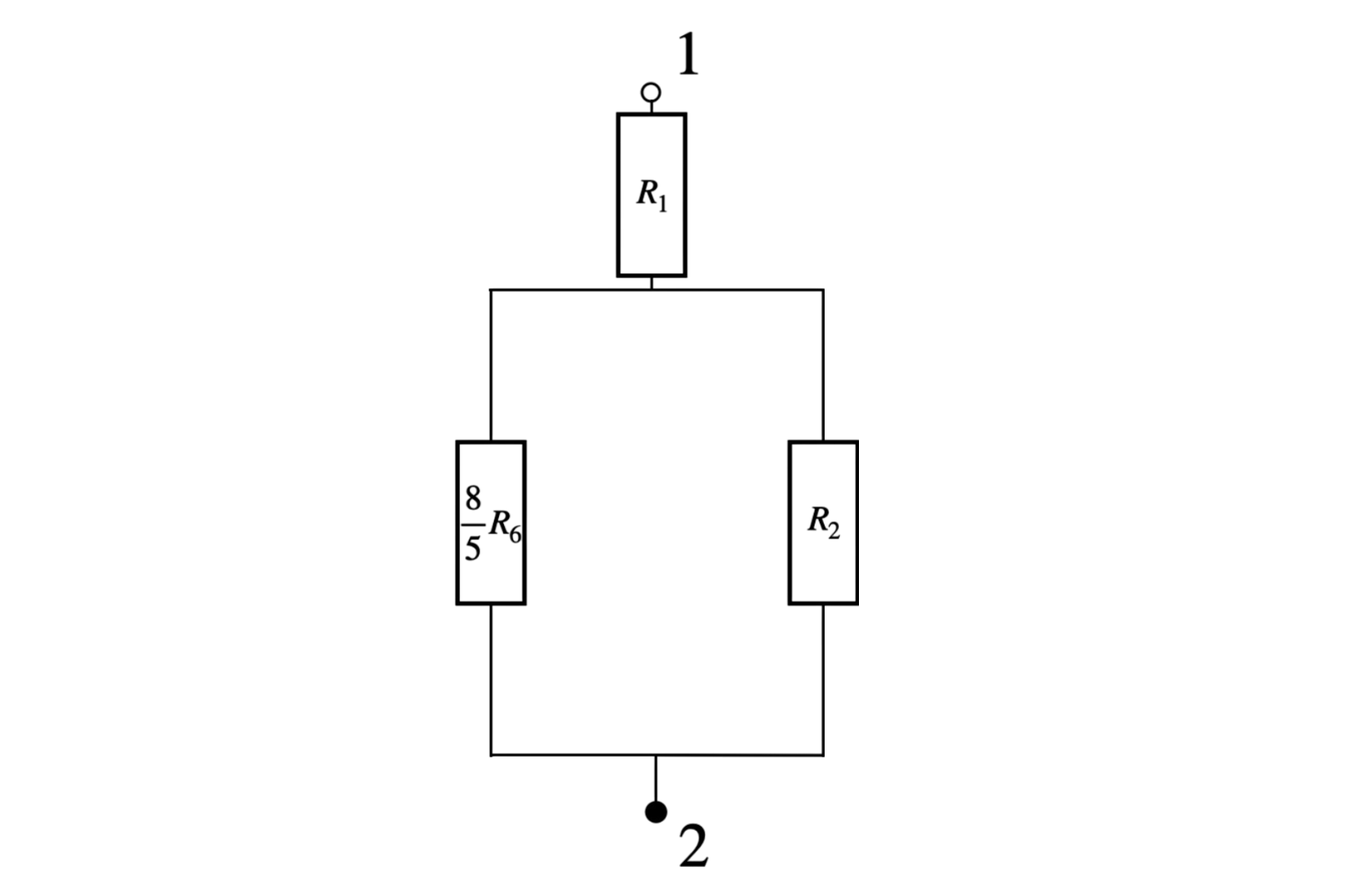
Krok 7: Zastępujemy oporniki \( R_2 \) i \(\frac{8}{5} R_6 \), jednym (którego wartość oporu zastępczego będzie wynosić \(\frac{8}{13} R_6\), ponieważ są połączone równolegle). Otrzymujemy:

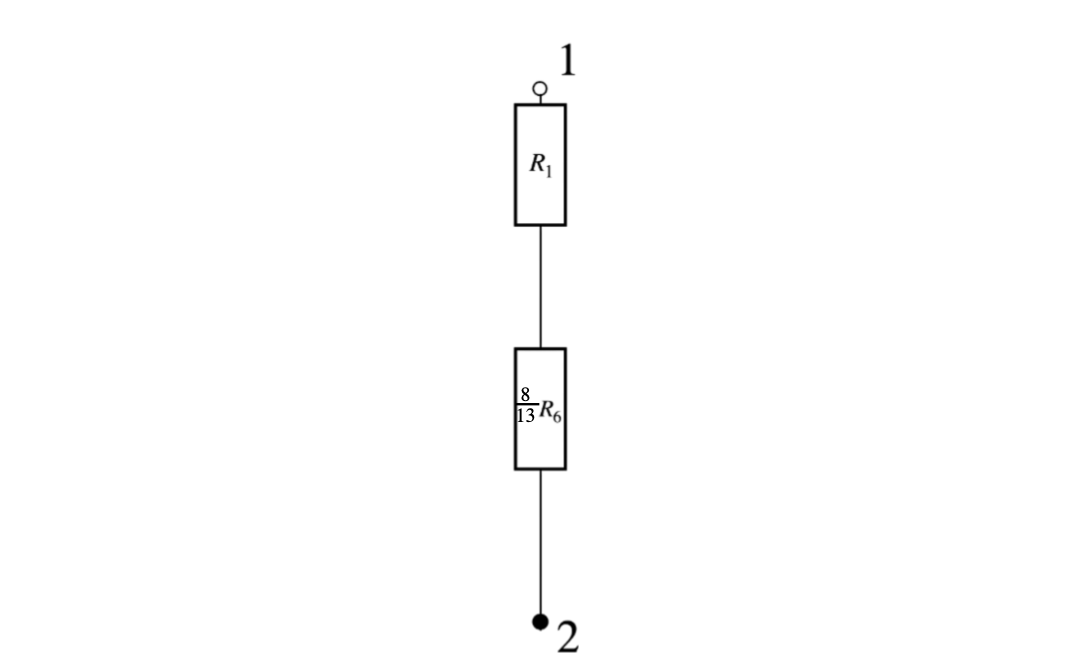
Krok 9: Zastępujemy oporniki \( R_1 \) i \(\frac{8}{13} R_6 \), jednym (którego wartość oporu zastępczego będzie wynosić \(\frac{21}{13} R_6\), ponieważ są połączone szeregowe). Otrzymujemy:

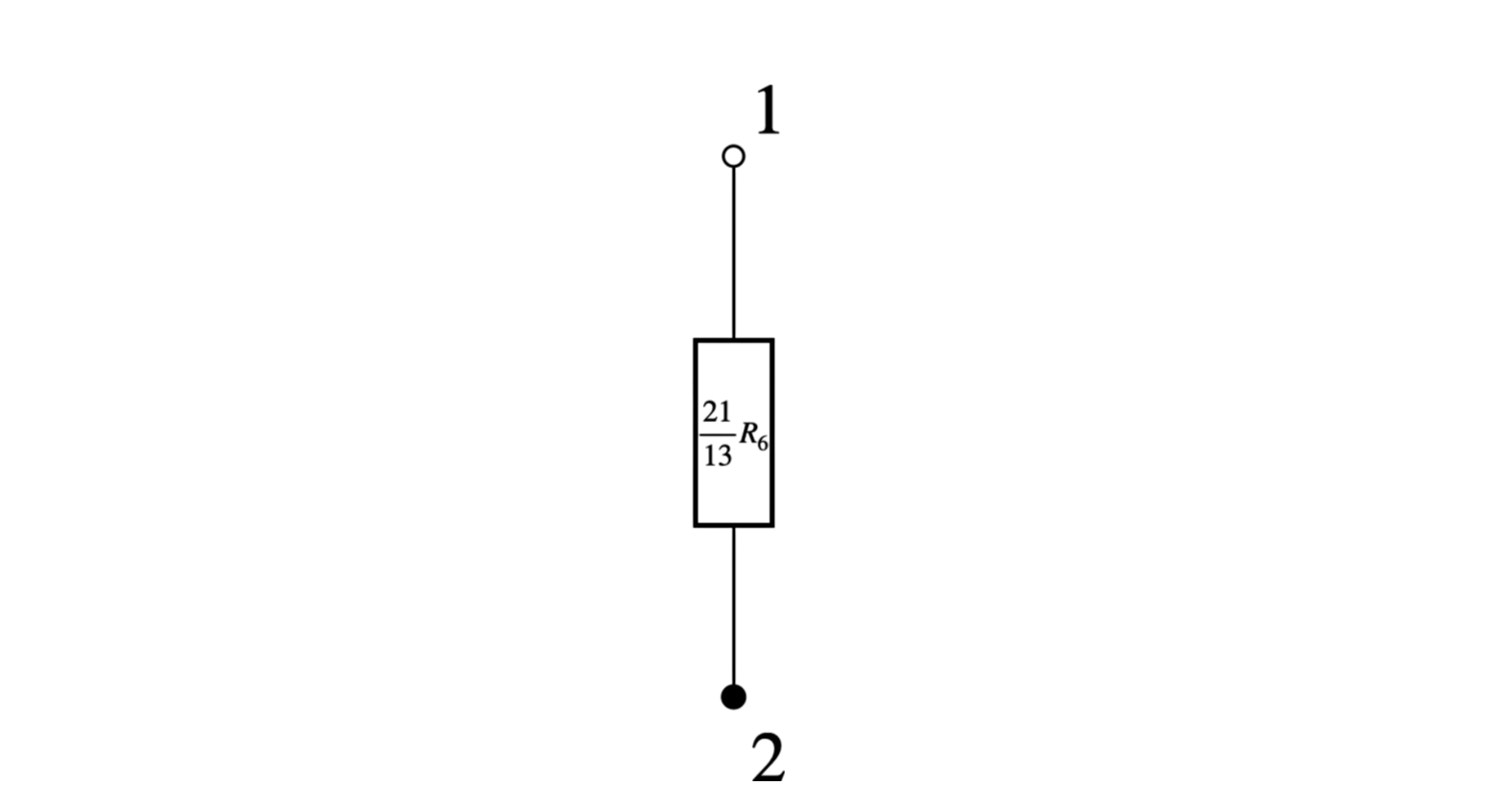
Odpowiedź: Opór zastępczy wynosi: \(\frac{21}{13} R_6\), gdzie \(R_6\) jest wartością oporu jednego opornika (Zgodnie z treścią naszego zadania, że wszytskie oporniki mają opór o tej samej wartości).