A
A-
A
A+
  2. Kalkulatory
  3. Wzory Fizyczne
  4. Przeliczniki
  5. Notatki
  6. Nauka
  7. Zadania
Spis Treści
1. Wstęp do Pierwszej Prędkości Kosmicznej 2. Wyprowadzenie Wzoru 3. Zastosowanie Pierwszej Prędkości Kosmicznej 4. Satelity Geostacjonarne 5. Obliczenia i Przykłady

Spis Treści

Pierwsza Prędkość Kosmiczna

Pierwsza prędkość kosmiczna jest kluczowym pojęciem w fizyce orbitalnej. Opisuje minimalną prędkość, jaką ciało musi osiągnąć, aby znaleźć się na stabilnej orbicie wokół planety, bez dodatkowego napędu.

1. Wstęp do Pierwszej Prędkości Kosmicznej

Każde ciało na orbicie porusza się dzięki równowadze między siłą grawitacji, która działa jako siła przyciągająca, a siłą dośrodkową wynikającą z ruchu orbitalnego. Ta prędkość minimalna, zwana pierwszą prędkością kosmiczną, umożliwia satelitom i innym obiektom swobodne okrążanie planety bez spadania na jej powierzchnię.

2. Wyprowadzenie Wzoru

Pierwsza prędkość kosmiczna wynika z warunku równowagi między siłą grawitacji a siłą dośrodkową. Z wyliczeń na podstawie równania sił, otrzymujemy:

\( v_1 = \sqrt{\frac{G M}{R}} \)
Pokaż wyprowadzenie wzoru
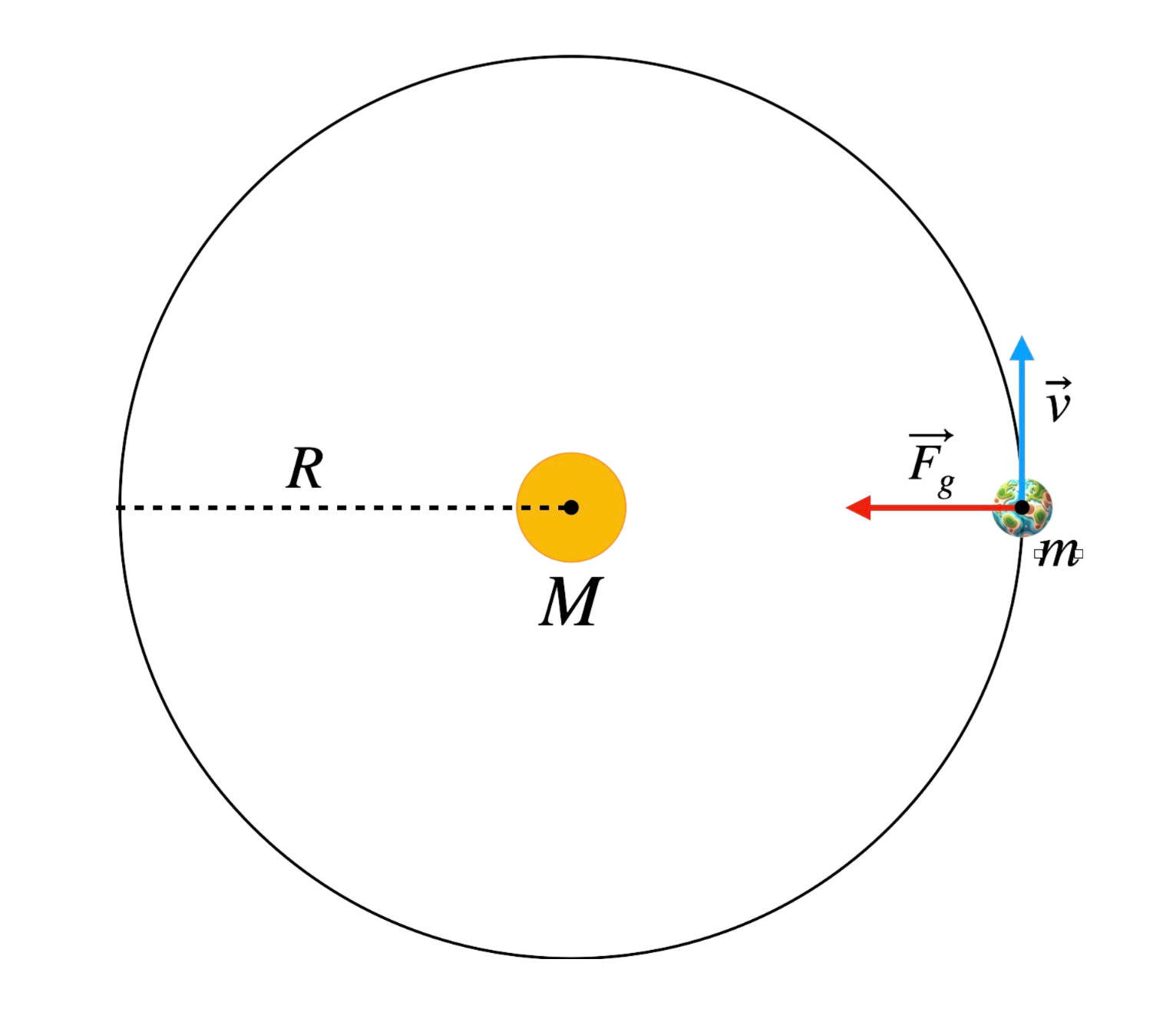
Pierwsza Prędkość Kosmiczna

Pierwsza prędkość kosmiczna \( v_1 \) jest wyprowadzana z warunku równowagi między siłą grawitacji \( F_g \) a siłą dośrodkową \( F_d \). Siła grawitacji wyrażona wzorem:

\( F_g = \frac{G M m}{R^2} \)

gdzie \( G \) to stała grawitacji, \( M \) masa Ziemi, \( R \) promień Ziemi, a \( m \) masa satelity. Siła dośrodkowa jest dana wzorem:

\( F_d = m \frac{v_1^2}{R} \)

Porównując obie siły, otrzymujemy:

\( \frac{G M m}{R^2} = m \frac{v_1^2}{R} \)

Uproszczenie prowadzi do wzoru na pierwszą prędkość kosmiczną:

\( v_1 = \sqrt{\frac{G M}{R}} \)

Wartość \( v_1 \) dla Ziemi wynosi około \( 7,91 \, \text{km/s} \), co obliczamy dla \( R = 6,371 \cdot 10^6 \, \text{m} \) i \( M = 5,972 \cdot 10^{24} \, \text{kg} \).

3. Zastosowanie Pierwszej Prędkości Kosmicznej

Dzięki pierwszej prędkości kosmicznej możliwe jest umieszczanie satelitów na niskich orbitach okołoziemskich (LEO), takich jak satelity GPS czy stacja kosmiczna ISS. Przy prędkości \( v_1 \) obiekty poruszają się po niemal idealnych kołowych orbitach.

4. Satelity Geostacjonarne

Satelity geostacjonarne znajdują się na orbicie, która pozwala im pozostać nieruchomymi względem powierzchni Ziemi. Aby wyznaczyć wysokość orbity, możemy skorzystać z równowagi sił grawitacyjnej i dośrodkowej.

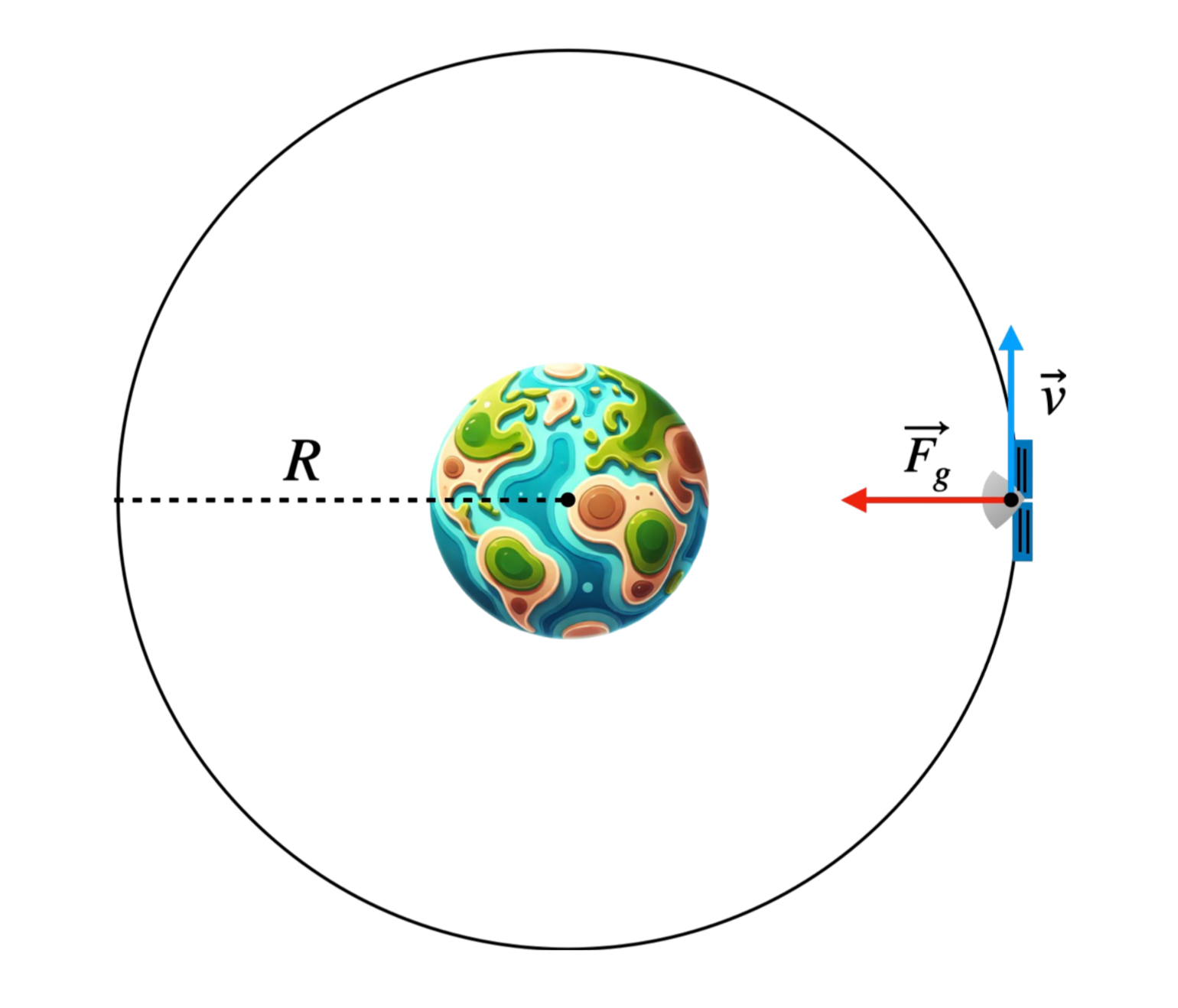
Satelita Geostacjonana
Pokaż wyprowadzenie wzoru

Siła grawitacyjna działająca na satelitę wynosi:

\( F_\text{g} = \frac{GMm}{r^2} \)

Z kolei siła dośrodkowa, utrzymująca satelitę na orbicie, to:

\( F_\text{c} = \frac{mv^2}{r} \)

Ponieważ prędkość satelity na orbicie to \( v = \frac{2 \pi r}{T} \), gdzie \( T = 86,400 \, \text{s} \), możemy podstawić to do równania i wyznaczyć promień orbity. Z równowagi sił mamy:

\( \frac{GMm}{r^2} = \frac{m \left( \frac{2 \pi r}{T} \right)^2}{r} \)

Po uproszczeniu i rozwiązaniu równania względem \( r \), otrzymujemy:

\( r = \sqrt[3]{\frac{GMT^2}{4 \pi^2}} \)

Podstawiając wartości, uzyskujemy promień orbity geostacjonarnej:

\( R_\text{geo} \approx 42,164 \, \text{km} \)

Wysokość orbity geostacjonarnej \( h \) to różnica pomiędzy promieniem orbity a promieniem Ziemi \( R \):

\( h = R_\text{geo} - R \approx 35,786 \, \text{km} \)

5. Obliczenia i Przykłady

Przykład: Oblicz prędkość orbitalną satelity na orbicie geostacjonarnej. Wzór na prędkość orbitalną:

\( v = \sqrt{\frac{G M}{R_\text{geo}}} \)

Po podstawieniu wartości dla \( R_\text{geo} \), \( G \), i \( M \), otrzymujemy:

\( v \approx 3,07 \, \text{km/s} \)

Satelita geostacjonarny porusza się z prędkością około \( 3,07 \, \text{km/s} \) na wysokości \( 35,786 \, \text{km} \) nad powierzchnią Ziemi (w odległości \( 42,164 \, \text{km} \) od środka Ziemi).