A
A-
A
A+
  2. Kalkulatory
  3. Wzory Fizyczne
  4. Przeliczniki
  5. Notatki
  6. Nauka
  7. Zadania
Spis Treści
1. Praca Stała 2. Przykłady Pracy 3. Przykład Zadania 4. Praca w Ruchu po Okręgu 5*. Praca Zmiennej Siły 6. Zastosowanie

Spis treści

Praca w Fizyce

Praca to wielkość fizyczna, która opisuje ilość energii przekazywanej poprzez siłę działającą na ciało podczas ruchu. W przypadku prostoliniowego ruchu ciała, pracę możemy przedstawić jako iloczyn skalarny siły \(\vec{F}\) i przemieszczenia \(\vec{\Delta r}\) :

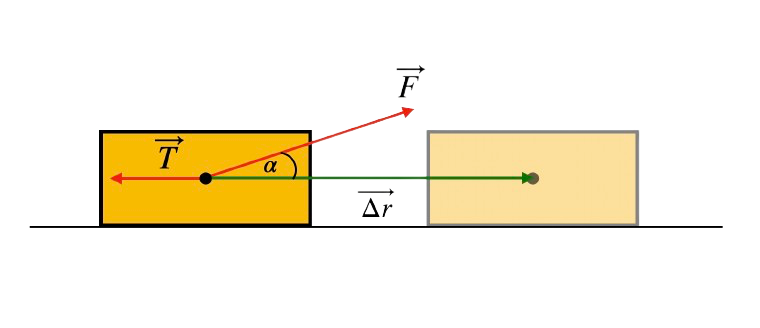
Praca wykonana podczas przesuwania ciała działając siłą pod kątem
\( W = \vec{F} \cdot \vec{\Delta r} \)
\( W = F \Delta r \cos(\alpha) \)

gdzie:

  • \(\alpha \) – kąt alpha pomiędzy wektorem siły i przemieszczenia

Jednostką pracy jest dżul \(J\) : \(1 J = 1 N \cdot 1 m = 1 \frac{kg \cdot m^2}{s^2}\)

1. Praca Stała

W przypadku, gdy stała siła \( F \) działa na ciało i powoduje jego przesunięcie o odległość \( s \), praca \( W \) wykonana przez siłę jest dana wzorem:

\( W = F \cdot s \cdot \cos(\alpha) \)

gdzie:

  • \( F \) – wartość siły,
  • \( s \) – odległość przebyta przez ciało,
  • \( \alpha \) – kąt między kierunkiem siły a kierunkiem ruchu.

2. Przykłady Obliczania Pracy dla Różnych Sił

Przypadek (a): Siła \( F \) działa pod kątem \( \alpha \), ruch ciała jest poziomy

W tym przypadku na ciało działają trzy siły:

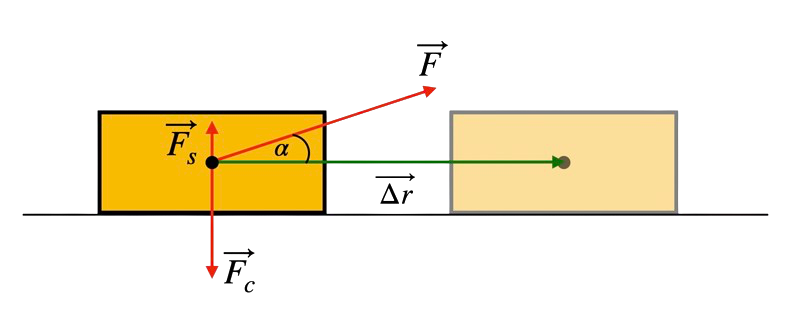
Praca wykonana podczas przesuwania ciała działając siłą pod kątem
  • Siła \( F \) pod kątem \( \alpha \) do kierunku przemieszczenia,
  • Siła ciężkości \( F_c \) prostopadła do przemieszczenia,
  • Siła sprężystości stołu \( F_s \), również prostopadła do przemieszczenia.

Praca wykonana przez siłę \( F \) jest równa:

\( W_F = F \cdot \Delta r \cdot \cos(\alpha) \)

Jeśli \( \alpha = 0^\circ \), praca wynosi:

\( W_F = F \cdot \Delta r \)

Praca siły ciężkości \( F_c \), która działa prostopadle do przemieszczenia (\( \alpha = 90^\circ \)), wynosi:

\( W_{F_c} = F_c \cdot \Delta r \cdot \cos(90^\circ) = 0 \)

Praca siły sprężystości \( F_s \) również wynosi:

\( W_{F_s} = F_s \cdot \Delta r \cdot \cos(90^\circ) = 0 \)

Przypadek (b): Podnoszenie ciała

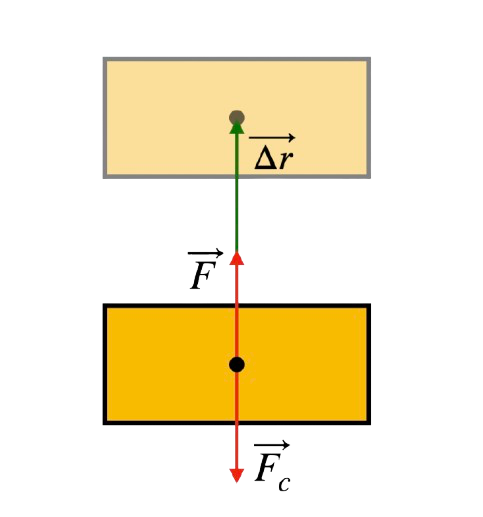
Praca wykonana podczas podnoszenia ciała działając siłą

Podczas podnoszenia ciała o masie \( m \) na wysokość \( h \), pracę wykonuje siła skierowana pionowo w górę. Zakładając, że podnoszenie odbywa się ze stałą prędkością, praca wykonana przez siłę zewnętrzną \( F \) równa się:

\( W = F \cdot h \)

Gdzie siła \( F \) musi być równa co do wartości sile ciężkości \( F_c = m \cdot g \), aby zrównoważyć masę ciała:

\( W = m \cdot g \cdot h \)

Jednocześnie, praca siły ciężkości \( F_c \) podczas podnoszenia ciała działa przeciwnie do kierunku przemieszczenia, więc jest równa:

\( W_{F_c} = -m \cdot g \cdot h \)

3. Przykład Zadania: Praca Sił Pod Kątem

Przykład: Dziecko ciągnie klocek po ziemi siłą \( F = 50 \, \text{N} \) pod kątem \( \alpha = 30^\circ \) względem poziomu. Klocek przemieszcza się o \( s = 5 \, \text{m} \) w poziomie. Siła tarcia między klockiem a podłożem wynosi \( T = 10 \, \text{N} \).

Oblicz pracę wykonaną przez siłę ciągnącą i pracę wykonaną przez siłę tarcia.

Pokaż rozwiązanie krok po kroku

Rozwiązanie:

Praca wykonana podczas przesuwania ciała działając siłą pod kątem

Krok 1: Znalezienie składowej siły \( F \) działającej w kierunku przesunięcia:

\( F_{\text{x}} = F \cdot \cos(\alpha) = 50 \cdot \cos(30^\circ) = 43.3 \, \text{N} \)

Krok 2: Obliczenie pracy wykonanej przez siłę ciągnącą:

\( W_F = F_{\text{x}} \cdot s = 43.3 \cdot 5 = 216.5 \, \text{J} \)

Krok 3: Obliczenie pracy wykonanej przez siłę tarcia (działa przeciwnie do kierunku ruchu, więc praca będzie ujemna):

\( W_f = -f \cdot s = -10 \cdot 5 = -50 \, \text{J} \)

Odpowiedź: Praca wykonana przez siłę ciągnącą wynosi \( 216.5 \, \text{J} \), a praca wykonana przez siłę tarcia wynosi \( -50 \, \text{J} \).

4. Praca w Ruchu po Okręgu

W ruchu po okręgu siła dośrodkowa działa prostopadle do kierunku prędkości ciała ( \(\alpha = 90^\circ\) ) w każdym momencie, przez co nie wykonuje pracy. Wynika to z faktu, że nie występuje przesunięcie wzdłuż kierunku siły dośrodkowej.

\( W = F_d \cdot s \cdot \cos(\alpha) = F_d \cdot s \cdot 0 = 0\)

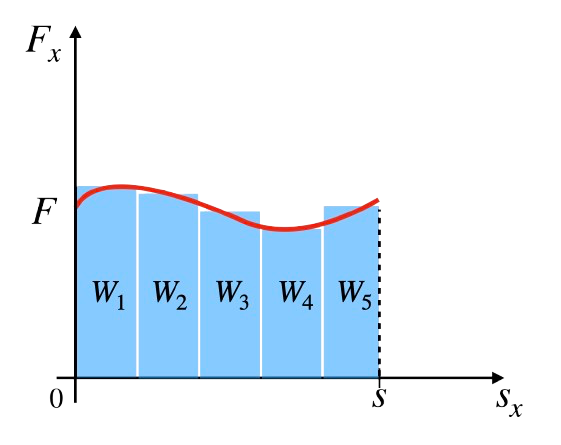
5. Praca wykonana przez zmienną siłę

W przypadku zmiennej siły, która jest nachylona pod kątem 0° do toru ruchu ciała, praca wykonana przez tę siłę jest równa polu powierzchni pod wykresem \( F(x) \). Możemy to zapisać za pomocą całki, gdzie praca \( W \) jest określona jako całkowite pole pod wykresem siły w zależności od przemieszczenia:

Wykres zależności siły od drogi
\( W = \int F(x) \, dx \)
\( W \approx W_1 + W_2 + ... \)

6. Zastosowania pracy w codziennym życiu

Praca jest jednym z podstawowych pojęć fizycznych, które ma szerokie zastosowanie w wielu dziedzinach życia codziennego. Oto kilka przykładów:

  • Transport: W przypadku podnoszenia lub przesuwania ciężarów, praca jest wykonywana przez siły, które działają na obiekt. Na przykład, unoszenie torby na wzniesienie lub ciągnięcie wózka na zakupy wymaga wykonania pracy przez siłę działającą na obiekt.
  • Ruch pojazdów: Praca jest wykonywana przez silnik pojazdu, który przekazuje energię na koła. W ten sposób pojazd pokonuje opory, takie jak tarcie i opór powietrza.
  • Winda: Winda podnosząca pasażerów na wyższe piętra budynku również wykorzystuje pracę wykonaną przez siłę elektryczną, która unosi kabinę windy.
  • Przemiany energii: Wiele urządzeń, takich jak pompy, klimatyzatory czy urządzenia grzewcze, wykorzystuje energię w postaci pracy do przemiany energii mechanicznej, cieplnej lub elektrycznej w codziennych zadaniach.

Zrozumienie, jak praca jest wykonywana i przekazywana, pozwala nam na efektywne wykorzystanie energii w różnych aspektach życia.