1. Pierwsze Prawo Keplera

Pierwsze Prawo Keplera, znane jako prawo orbit eliptycznych, mówi, że planety poruszają się po elipsach, w których jedno z ognisk zajmuje Słońce.

Przykład: Ziemia okrąża Słońce po elipsie, której centrum nie pokrywa się z centrum Słońca.

2. Drugie Prawo Keplera

Drugie Prawo Keplera, prawo równego pola, mówi, że linia łącząca planetę i Słońce zakreśla równe pola w równych odstępach czasu. Oznacza to, że planety poruszają się szybciej, gdy są bliżej Słońca (w peryhelium), a wolniej, gdy są dalej (w aphelium).

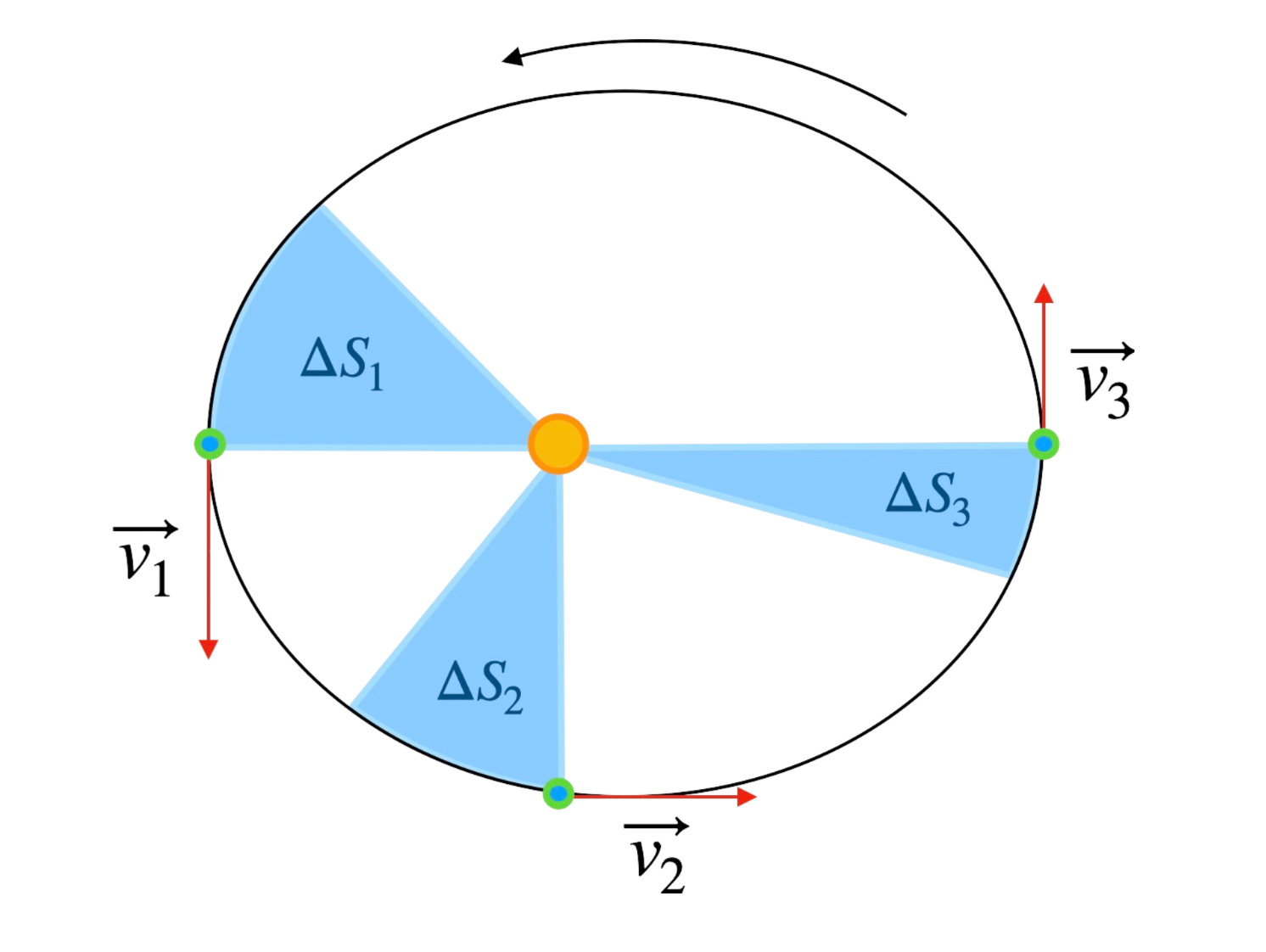
Zasada Zachowania Momentu Pędu

Drugie prawo Keplera można wyprowadzić w oparciu o zasadę zachowania momentu pędu planety względem Słońca. Obliczmy pole figury \( \Delta S \), które zakreśla promień wodzący planety w bardzo krótkim czasie \( \Delta t \). Planeta w początkowej chwili znajduje się w aphelium i w czasie \( \Delta t \) zakreśla tor o długości \( \Delta s = v \cdot \Delta t \).

Pole \( \Delta S \) tej figury jest w przybliżeniu równe polu trójkąta prostokątnego:

\[ \Delta S = \frac{1}{2} \cdot r \cdot d = \frac{1}{2} \cdot r \cdot v \cdot \Delta t \]

Jednocześnie moment pędu \( L \) planety obiegającej Słońce wynosi:

\[ L = m \cdot v \cdot r \]

Zatem:

\[ \Delta S = \frac{L}{2 \cdot m} \cdot \Delta t \]

Z równania wynika, że w jednakowych odstępach czasu \( \Delta t \), promień wodzący zakreśla figury o równych polach powierzchni \( \Delta S \). To oznacza, że moment pędu planety również pozostaje stały (\( L = \text{const} \)).

Drugie prawo Keplera jest więc konsekwencją zasady zachowania momentu pędu planety względem Słońca.

Przykład: Ziemia porusza się szybciej zimą (kiedy jest bliżej Słońca), niż latem (kiedy jest dalej).

3. Trzecie Prawo Keplera

Trzecie Prawo Keplera opisuje zależność między okresem orbitalnym a wielką półosią elipsy orbity. Mówi ono, że kwadrat okresu obiegu planety wokół Słońca jest proporcjonalny do sześcianu wielkiej półosi orbity:

gdzie:

• \( T \) – okres orbitalny,
• \( r \) – średnia odległość od środka.

Przykład: Planety dalej od Słońca (np. Saturn) mają dłuższe okresy orbitalne niż planety bliżej Słońca (np. Merkury).

4. Przykłady Zastosowań Praw Keplera

1. Ruch sztucznych satelitów

Prawa Keplera są stosowane do obliczeń orbitalnych satelitów, które krążą wokół Ziemi, korzystając z zasad trzeciego prawa do ustalania ich okresów obiegu.

2. Odkrywanie egzoplanet

Na podstawie analizy ruchu gwiazd wywołanego przez siły grawitacyjne planet, astronomowie stosują prawa Keplera do określania mas i orbit egzoplanet.

3. Planowanie misji kosmicznych

Trajektorie sond kosmicznych są projektowane z uwzględnieniem praw Keplera, co pozwala na precyzyjne ustalanie momentów startu i osiągania orbit docelowych.