Prawa Kirchhoffa
Prawa Kirchhoffa stanowią fundamentalne zasady analizy obwodów elektrycznych, umożliwiając obliczanie prądów i napięć w skomplikowanych układach. Składają się z dwóch głównych zasad: pierwszego prawa (prawo węzłów) i drugiego prawa (prawo oczek).
1. Wstęp
Prawa Kirchhoffa opisują zachowanie prądów i napięć w obwodach elektrycznych. Są szeroko stosowane w analizie układów zarówno liniowych, jak i nieliniowych. Zrozumienie ich zastosowania pozwala na skuteczne rozwiązywanie problemów związanych z rozkładem energii elektrycznej.
2. Pierwsze Prawo Kirchhoffa
Pierwsze Prawo Kirchhoffa, znane również jako prawo węzłów, mówi, że suma prądów wpływających do węzła jest równa sumie prądów wypływających z węzła:
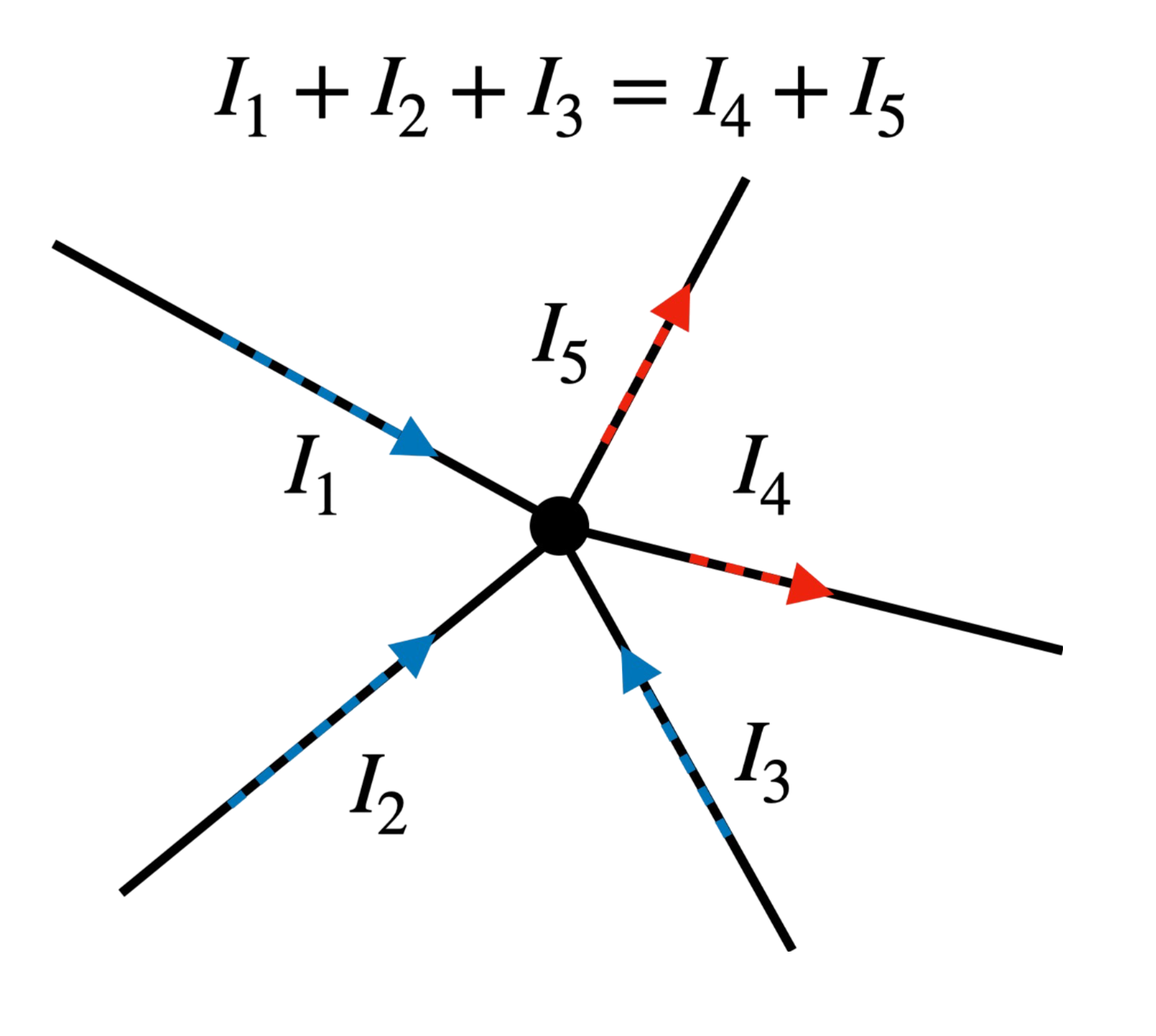
3. Drugie Prawo Kirchhoffa
Drugie Prawo Kirchhoffa, znane również jako prawo oczek, mówi, że suma napięć w dowolnym oczku obwodu jest równa zeru:
Oznacza to, że suma przyrostów i spadków napięcia w zamkniętej pętli wynosi zero.
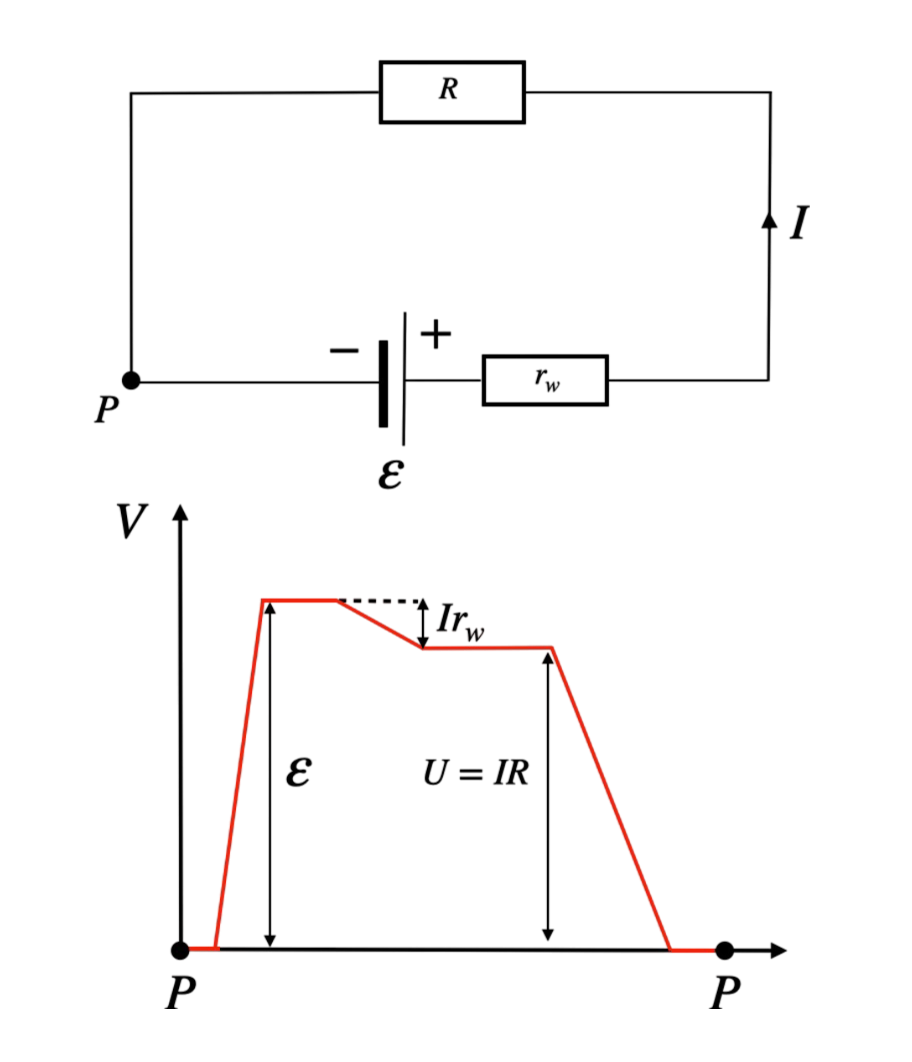
4. Przykład Zadania: Analiza Węzłów
Przykład: W obwodzie elektrycznym mamy węzeł, do którego wpływają prądy \( I_1 = 2 \, A \) oraz \( I_2 = 3 \, A \), a wypływają \( I_3 \) oraz \( I_4 = 4 \, A \). Oblicz wartość prądu \( I_3 \).
Rozwiązanie:
Krok 1: Zapisujemy równanie zgodnie z pierwszym prawem Kirchhoffa:
Krok 2: Podstawiamy wartości znanych prądów:
Krok 3: Obliczamy wartość \( I_3 \):
Odpowiedź: Prąd \( I_3 \) wynosi \( 1 \, A \).
5. Przykład Zadania: Analiza Oczek
Zadanie: W zamkniętej pętli obwodu napięcia wynoszą: \( U_1 = 10 \, V \), \( U_2 = 5 \, V \), a spadki napięcia na rezystorach wynoszą \( U_R = 12 \, V \). Sprawdź zgodność z drugim prawem Kirchhoffa.
Rozwiązanie:
Krok 1: Zapisujemy równanie zgodnie z drugim prawem Kirchhoffa:
Krok 2: Podstawiamy wartości znanych napięć:
Krok 3: Sprawdzamy zgodność równania:
Wynik pokazuje, że równanie nie jest spełnione. Oznacza to, że w układzie występuje błąd pomiaru lub założenie dotyczące wartości napięć jest nieprawidłowe.