Prawo Archimedesa, wzory i teoria

1. Wstęp

Pewnego dnia, ponad 2000 lat temu, grecki uczony Archimedes otrzymał ciekawe zadanie od króla Syrakuz. Miał sprawdzić, czy korona króla jest wykonana w całości z czystego złota, nie niszcząc jej przy tym. Podczas kąpieli w wannie Archimedes zauważył, że jego ciało staje się lżejsze, a woda wylewa się z wanny. Nagle krzyknął „Eureka!”, odkrywając prawo, które dziś znamy jako Prawo Archimedesa.

Prawo to dotyczy siły wyporu działającej na obiekty zanurzone w cieczy lub gazie i wyjaśnia, dlaczego przedmioty pływają lub toną. To odkrycie miało ogromne znaczenie w fizyce i inżynierii, zwłaszcza w projektowaniu statków i łodzi podwodnych.

2. Prawo Archimedesa

Prawo Archimedesa mówi, że na każde ciało zanurzone w płynie działa siła wyporu, która jest równa ciężarowi wypartego płynu. Oznacza to, że jeśli zanurzymy przedmiot w wodzie, woda „wypiera” przedmiot, a siła wyporu zależy od objętości przedmiotu i gęstości płynu.

Matematykę tego prawa można wyrazić prostym wzorem:

\( F_w = \rho_f \cdot g \cdot V \)

Gdzie:

\( F_w \) – siła wyporu
\( \rho_f \) – gęstość cieczy
\( g \) – przyspieszenie grawitacyjne
\( V \) – objętość zanurzonego ciała

3. Wyprowadzenie wzoru

Siła wyporu powstaje na skutek różnicy ciśnień hydrostatycznych działających na górną i dolną powierzchnię ciała zanurzonego w cieczy. Górna powierzchnia znajduje się na mniejszej głębokości, gdzie ciśnienie jest niższe, a dolna na większej głębokości, gdzie ciśnienie jest wyższe. Ta różnica ciśnień generuje siłę wyporu.

\( F_w = F_{\text{dolna}} - F_{\text{górna}} \)

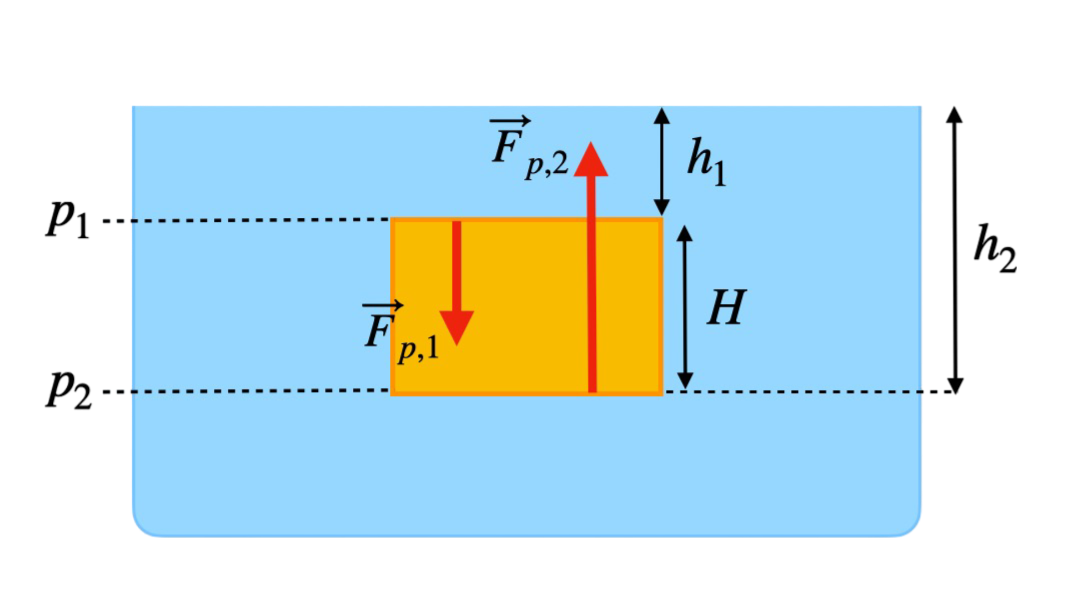
Ciśnienie hydrostatyczne wyrażamy wzorem \( p = \rho \cdot g \cdot h \). Siły parcia działające na górną i dolną podstawę ciała można zapisać jako:

\( F_{p,1} = \rho \cdot g \cdot h_1 \cdot S \)

\( F_{p,2} = \rho \cdot g \cdot h_2 \cdot S \)

Zatem siła wyporu \( F_w \) wynosi:

\( F_w = F_{p,2} - F_{p,1} \)

Podstawiamy za \( F_{p,2} \) i \( F_{p,1} \) wyrażenia dla sił parcia:

\( F_w = (\rho \cdot g \cdot h_2 \cdot S) - (\rho \cdot g \cdot h_1 \cdot S) \)

Wyłączając wspólne czynniki \( \rho \cdot g \cdot S \), otrzymujemy:

\( F_w = \rho \cdot g \cdot S \cdot (h_2 - h_1) \)

Ponieważ \( h_2 - h_1 = H \), gdzie \( H \) to wysokość zanurzonej części ciała, a \( S \cdot H = V \) jest objętością zanurzonego ciała, wzór upraszcza się do:

\( F_w = \rho \cdot g \cdot V \)

Wyprowadzone równanie pokazuje, że siła wyporu jest równa ciężarowi wypartej cieczy.

4. Zadanie

Zadanie: Oblicz siłę wyporu działającą na drewnianą belkę o objętości \( V = 0.5 \, \text{m}^3 \) zanurzoną w wodzie o gęstości \( \rho_f = 1000 \, \text{kg/m}^3 \).

Pokaż rozwiązanie krok po kroku

Rozwiązanie:

Krok 1: Zidentyfikuj dane: \( V = 0.5 \, \text{m}^3 \), \( \rho_f = 1000 \, \text{kg/m}^3 \), \( g = 9.81 \, \text{m/s}^2 \).

Krok 2: Zastosuj wzór na siłę wyporu:

\( F_w = \rho_f \cdot g \cdot V \)

Krok 3: Podstaw wartości:

\( F_w = 1000 \, \text{kg/m}^3 \cdot 9.81 \, \text{m/s}^2 \cdot 0.5 \, \text{m}^3 = 4905 \, \text{N} \)

Odpowiedź: Siła wyporu działająca na belkę wynosi \( 4905 \, \text{N} \).

5. Zastosowania w życiu

Prawo Archimedesa ma szerokie zastosowania w codziennym życiu i technologii:

Statki i łodzie: Dzięki sile wyporu nawet ogromne statki mogą unosić się na wodzie, mimo że ich masa jest ogromna.
Łodzie podwodne: Mogą zanurzać się i wypływać na powierzchnię, regulując swoją gęstość poprzez wpompowywanie lub wypompowywanie wody z balastów.
Balony na gorące powietrze: Gorące powietrze wewnątrz balonu jest mniej gęste niż powietrze otaczające, co powoduje siłę wyporu i wznoszenie się balonu.
Pływanie: Ludzie i zwierzęta mogą unosić się w wodzie dzięki sile wyporu.