Spis Treści
1. Wstęp 2. Prawo Coulomba 3. Przykładowe Zadanie 4. Zastosowania Prawa Coulomba

Spis treści

Prawo Coulomba

1. Wstęp

W świecie fizyki istnieją dwa rodzaje ładunków: dodatnie i ujemne. Jednostką ładunku elektrycznego jest kulomb (C), a najmniejsza wartość ładunku, którą można zaobserwować w przyrodzie, to ładunek elementarny, wynoszący \( e = 1.602 \times 10^{-19} \, \text{C} \). Ładunki o przeciwnych znakach przyciągają się, a te o tych samych znakach odpychają. Materiały mogą być:

  • - Przewodnikami, w których ładunki swobodnie się poruszają (np. metale).
  • - Izolatorami, które nie przewodzą ładunku (np. szkło, plastik).
  • - Półprzewodnikami, zachowującymi się pośrednio między przewodnikami a izolatorami (np. krzem).

Aby zrozumieć siły między ładunkami, naukowiec Charles-Augustin de Coulomb sformułował Prawo Coulomba.

2. Prawo Coulomba

Prawo Coulomba opisuje siłę elektrostatyczną między dwoma punktowymi ładunkami. Siła ta jest proporcjonalna do iloczynu wartości ładunków i odwrotnie proporcjonalna do kwadratu odległości między nimi:

\( F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \)

Gdzie:

  • \( F \) – siła elektrostatyczna (N)
  • \( q_1, q_2 \) – wartości ładunków (C)
  • \( r \) – odległość między ładunkami (m)
  • \( k \) – stała proporcjonalności zwana stałą elektrostatyczną
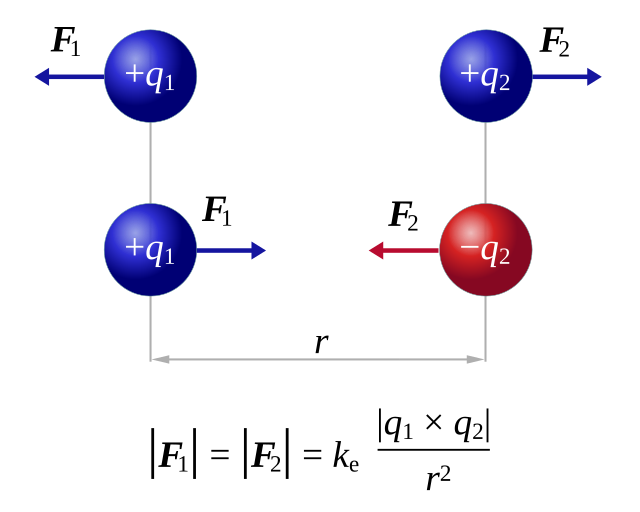
Prawo Coulumba

Źródło: Dna-Dennis

Stała elektrostatyczna w próżni wynosi:

\( k = \frac{1}{4 \pi \varepsilon_0} \approx 8.99 \times 10^9 \, \text{N·m}^2/\text{C}^2 \)

Gdzie \( \varepsilon_0 = 8.85 \times 10^{-12} \, \text{F/m} \) to przenikalność elektryczna próżni. W innych materiałach wzór zmienia się na:

\( k = \frac{1}{4 \pi \varepsilon} \)

Dla dwóch ładunków \( q_1 = q_2 = 1 \, \text{C} \) oddalonych o \( r = 1 \, \text{m} \), siła elektrostatyczna wynosi:

\( F = 8.99 \times 10^9 \, \text{N} \)

Jest to ogromna siła w porównaniu do grawitacji, która dla takich mas jest praktycznie niezauważalna. Siła elektrostatyczna może przyciągać lub odpychać, w przeciwieństwie do siły grawitacyjnej, która zawsze powoduje przyciąganie się ciał.

3. Przykładowe Zadanie

Zadanie: Dwa ładunki punktowe \( q_1 = 2 \, \mu\text{C} \) oraz \( q_2 = -3 \, \mu\text{C} \) znajdują się w odległości \( r = 0.5 \, \text{m} \). Oblicz wartość siły elektrostatycznej między nimi. Określ, czy ładunki się będą przyciągać, czy odpychać?

Pokaż rozwiązanie krok po kroku

Rozwiązanie:

Krok 1: Zidentyfikuj dane z zadania: \( q_1 = 2 \times 10^{-6} \, \text{C} \), \( q_2 = -3 \times 10^{-6} \, \text{C} \), \( r = 0.5 \, \text{m} \).

Krok 2: Zastosuj wzór na siłę elektrostatyczną:

\( F = k \cdot \frac{|q_1 \cdot q_2|}{r^2} \)

Krok 3: Podstaw wartości:

\( F = 8.99 \times 10^9 \cdot \frac{|(2 \times 10^{-6}) \cdot (-3 \times 10^{-6})|}{(0.5)^2} \)
\( F = 8.99 \times 10^9 \cdot \frac{6 \times 10^{-12}}{0.25} = 0.215 \, \text{N} \)

Odpowiedź: Siła elektrostatyczna między ładunkami wynosi \( F = 0.215 \, \text{N} \). Ładunki są różnoimienne (mają przeciwne znaki), zatem będą się przyciągać.

4. Zastosowania Prawa Coulomba

Prawo Coulomba znajduje zastosowanie w wielu dziedzinach, takich jak:

  • - Projektowanie kondensatorów: Obliczanie oddziaływań między ładunkami w układach elektrycznych.
  • Elektryczność statyczna: Analiza sił między naładowanymi ciałami.
  • - Modelowanie atomów: Opis sił między elektronami a jądrem atomowym.
  • - Systemy elektrostatyczne, takie jak drukarki laserowe czy separatory elektrostatyczne w przemyśle.