Prawo Pascala
1. Wstęp
Czym jest ciśnienie w płynach i jak przenosi się w zamkniętych naczyniach? To jedno z pytań, na które odpowiedź znalazł Blaise Pascal, francuski fizyk i matematyk. Odkrył on, że gdy wywieramy nacisk na ciecz lub gaz znajdujący się w zamkniętym pojemniku, zmiana ciśnienia rozchodzi się równomiernie we wszystkich kierunkach. Innymi słowy, wzrost ciśnienia spowodowany wywieraniem siły na ciecz lub gaz jest w każdym miejscu tego płynu jednakowy, niezależnie od kierunku działania siły. Ta obserwacja stała się podstawą jednego z najważniejszych praw hydrauliki – Prawa Pascala.
2. Prawo Pascala
Prawo Pascala mówi, że w zamkniętym naczyniu ciśnienie wywierane na ciecz lub gaz rozchodzi się równomiernie we wszystkich kierunkach i nie zmienia się przy przechodzeniu przez płyn. Mówiąc prościej, jeśli naciśniemy jedną stronę pojemnika, to ciśnienie wzrośnie w każdym punkcie cieczy o tę samą wartość. Prawa Pascala wyraża się wzorem:
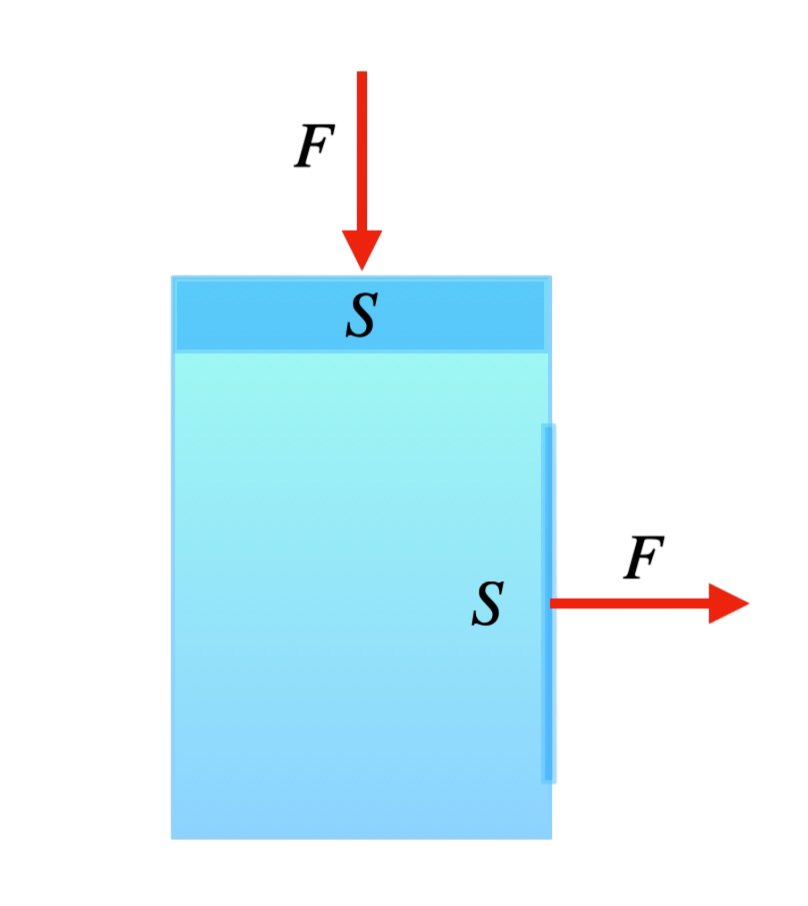
Dzięki temu prawu wiemy, że możemy zwiększyć ciśnienie nawet małym naciskiem na jedną część cieczy, co wywoła znaczący efekt w całym układzie. Z tego wynika ogromna praktyczność Prawa Pascala w urządzeniach takich jak prasy hydrauliczne czy hamulce samochodowe.
3. Przykładowe Zadanie
Zadanie: W zamkniętym naczyniu działamy siłą \( F = 50 \, \text{N} \) na tłok o powierzchni \( S = 0.1 \, \text{m}^2 \). Oblicz ciśnienie wywierane przez tłok na ciecz.
Rozwiązanie:
Krok 1: Zidentyfikuj dane z zadania: \( F = 50 \, \text{N} \) i \( S = 0.1 \, \text{m}^2 \).
Krok 2: Zastosuj wzór na ciśnienie:
Krok 3: Podstaw wartości:
Odpowiedź: Ciśnienie wywierane przez tłok na ciecz wynosi \( 500 \, \text{Pa} \).
4. Prasa Hydrauliczna
Jednym z najbardziej znanych zastosowań Prawa Pascala jest prasa hydrauliczna, urządzenie zbudowane z dwóch tłoków o różnych powierzchniach, połączonych wypełnioną cieczą komorą. Kiedy przykładamy siłę \( F_1 \) do mniejszego tłoka o powierzchni \( S_1 \), wywołujemy ciśnienie, które rozchodzi się równomiernie w całej cieczy.
Ponieważ ciśnienie w płynie jest stałe, mamy:
Oznacza to, że mniejsza siła wywierana na małym tłoku \( F_1 \) może wygenerować większą siłę \( F_2 \) na dużym tłoku, jeśli powierzchnia \( S_2 \) jest odpowiednio większa. W ten sposób możemy uzyskać znaczną siłę wyjściową przy niewielkim wysiłku, co jest przydatne przy podnoszeniu lub prasowaniu ciężkich przedmiotów.

5. Podnośnik Hydrauliczny – Zadanie
Zadanie: Chcemy podnieść samochód o masie 1500 kg za pomocą podnośnika hydraulicznego. Samochód stoi na większym tłoku o powierzchni \( S_2 = 0.5 \, \text{m}^2 \), a siła będzie przykładana do mniejszego tłoka o powierzchni \( S_1 = 0.01 \, \text{m}^2 \). Jaką siłę \( F_1 \) musimy wywrzeć na mniejszy tłok, aby unieść samochód?
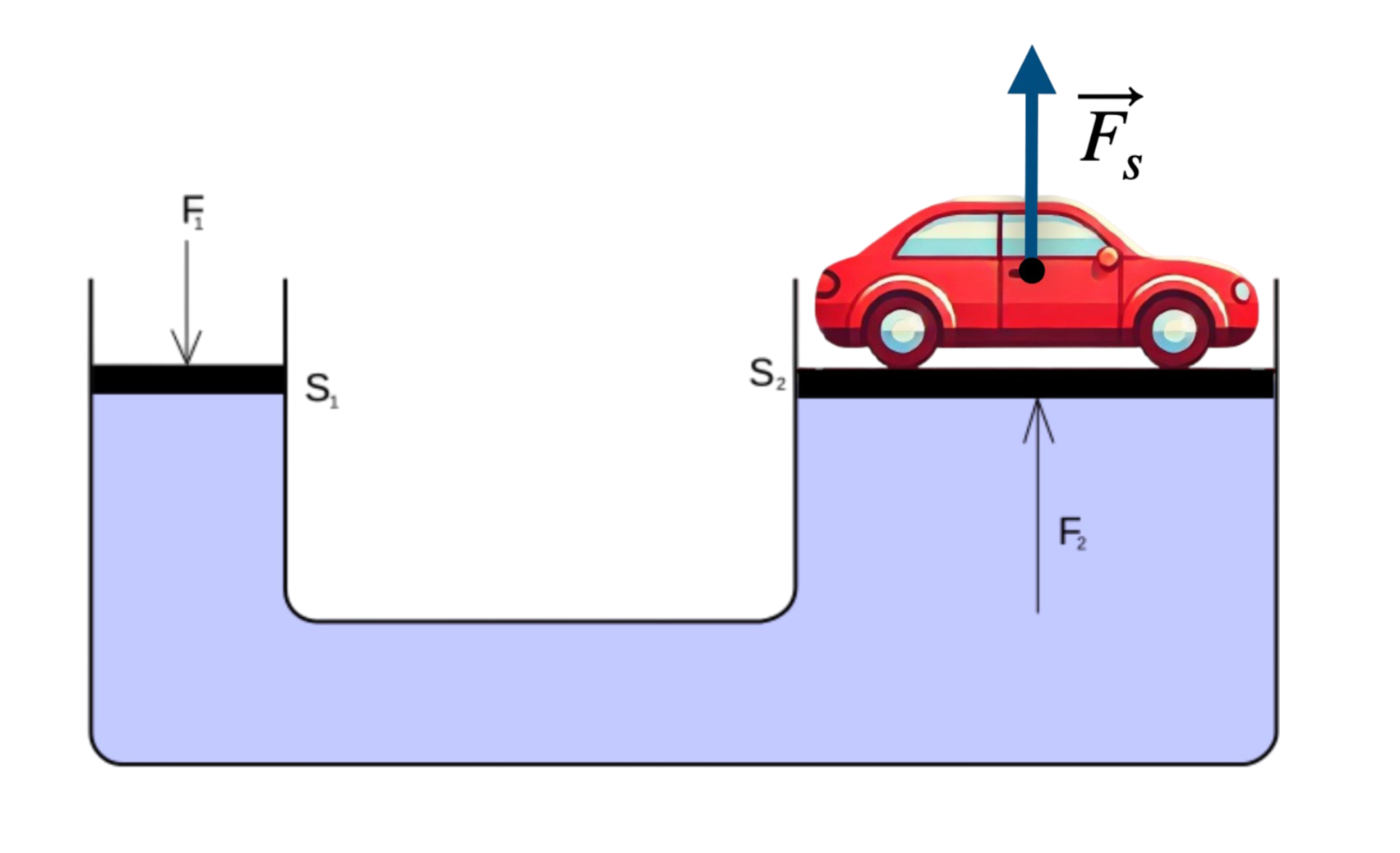
Rozwiązanie:
Krok 1: Oblicz siłę \( F_2 \), jaką musimy wywrzeć na większy tłok, aby unieść samochód. Siła ta odpowiada ciężarowi samochodu:
Krok 2: Zastosuj wzór wynikający z prawa Pascala:
Krok 3: Przekształć wzór, aby obliczyć \( F_1 \):
Krok 4: Podstaw wartości:
Odpowiedź: Aby podnieść samochód o masie 1500 kg, należy przyłożyć siłę \( F_1 = 294.3 \, \text{N} \) na mniejszy tłok.
6. Zastosowania Prawa Pascala
Prawo Pascala znajduje szerokie zastosowanie w wielu dziedzinach, zwłaszcza w technologii hydraulicznej, gdzie równomierny rozkład ciśnienia jest kluczowy do efektywnego działania. Oto kilka przykładów:
- Podnośniki hydrauliczne: Urządzenia te, stosowane na przykład w warsztatach samochodowych, umożliwiają podnoszenie dużych ciężarów, takich jak samochody. Niewielka siła przyłożona do małego tłoka generuje ciśnienie, które następnie przenosi się na większy tłok, podnosząc ciężki obiekt.
- Hamulce hydrauliczne: W samochodach pedał hamulca działa na ciecz w przewodach hydraulicznych, co z kolei powoduje równoczesny nacisk na klocki hamulcowe przy każdym kole. Dzięki temu samochód zatrzymuje się szybko i bezpiecznie, a siła rozłożona jest równomiernie.
- Prasy hydrauliczne: W zakładach przemysłowych prasy hydrauliczne wykorzystują Prawo Pascala do zgniatania lub kształtowania materiałów. Mała siła przyłożona do tłoka wywołuje ciśnienie, które przenosi się na większy tłok, umożliwiając generowanie bardzo dużych sił nacisku.
- Systemy zawieszenia hydraulicznego: Zawieszenia hydrauliczne, stosowane w niektórych ciężarówkach i autobusach, wykorzystują ciśnienie rozłożone równomiernie w całym systemie, co pozwala amortyzować wstrząsy i zapewnić płynność jazdy. Dzięki temu pojazdy są bardziej stabilne, a komfort podróży znacznie się zwiększa.