A-

A+

Spis Treści

1. Wstęp do Prawa Grawitacji 2. Wyprowadzenie Wzoru 3. Prawo Powszechnej Grawitacji 4. Zadanie 5. Skutki i Zastosowania

Spis treści

1. Wstęp do Prawa Grawitacji
2. Wyprowadzenie Wzoru
3. Prawo Powszechnej Grawitacji
4. Zadanie
5. Skutki i Zastosowania

Prawo Powszechnej Grawitacji

Prawo Powszechnej Grawitacji sformułowane przez Newtona opisuje uniwersalne oddziaływanie grawitacyjne pomiędzy dowolnymi dwoma ciałami posiadającymi masę. Siła ta odgrywa kluczową rolę w mechanice ciał niebieskich i ich ruchach w Układzie Słonecznym.

1. Wstęp do Prawa Grawitacji

Grawitacja to jedna z podstawowych sił w przyrodzie. Zgodnie z zasadami mechaniki klasycznej, działa ona zawsze jako siła przyciągająca, a jej wielkość zależy od mas ciał oraz odległości między nimi.

2. Wyprowadzenie Wzoru

Prawo Powszechnej Grawitacji Newtona opisuje siłę przyciągania między dowolnymi ciałami o masach \( m_1 \) i \( m_2 \), które są od siebie oddalone o odległość \( r \):

\[ F = G \cdot \frac{m_1 \cdot m_2}{r^2} \]

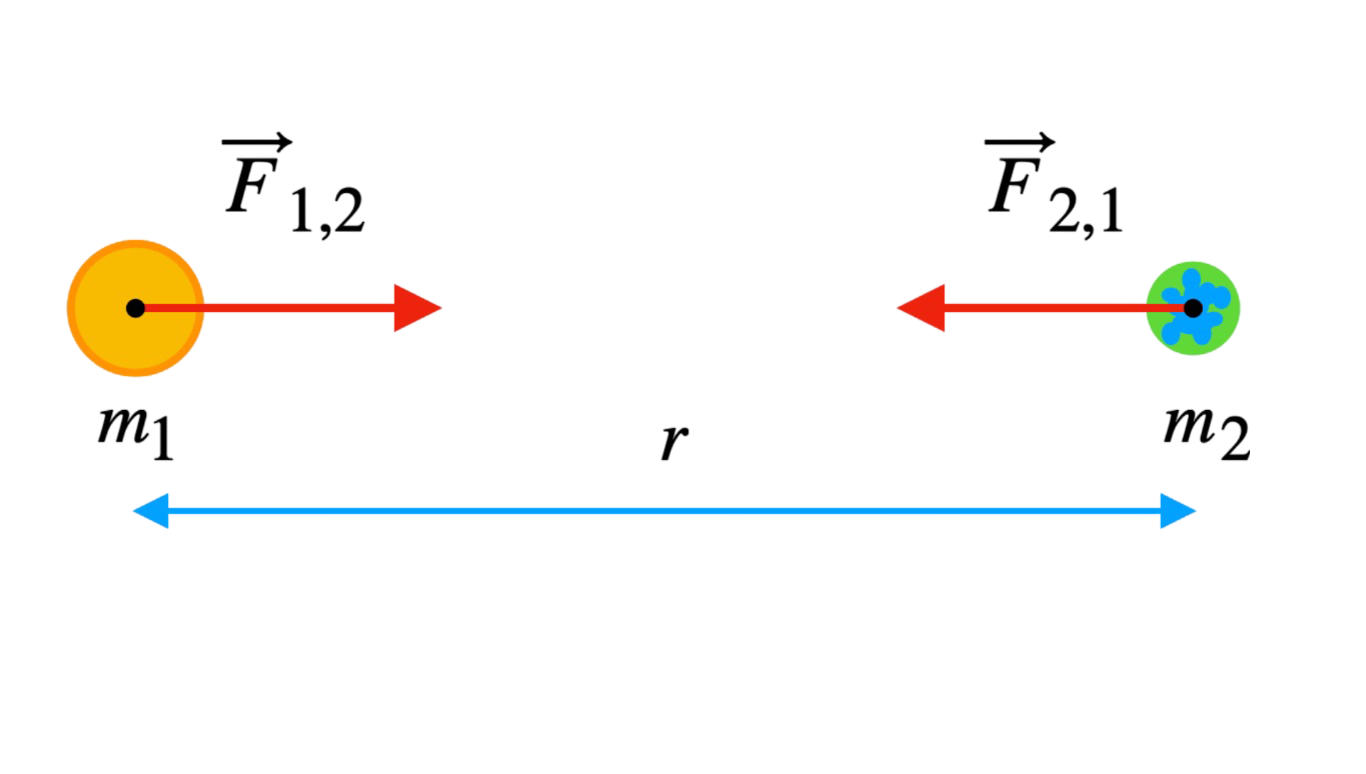
Ten wzór wskazuje, że siła jest proporcjonalna do iloczynu mas i odwrotnie proporcjonalna do kwadratu odległości.

Pokaż wyprowadzenie wzoru

Zacznijmy od trzeciego Prawa Keplera, które mówi, że stosunek kwadratu okresu orbitalnego \( T^2 \) do sześcianu promienia orbity \( r^3 \) jest stały dla wszystkich planet obiegających Słońce:

\[ \frac{T^2}{r^3} = \text{const} \]

To oznacza, że czas obiegu planety zależy od odległości od Słońca. Jeśli założymy, że siła przyciągająca Słońca (siła grawitacji) jest jedyną siłą, która utrzymuje planetę na orbicie, musi ona zapewniać siłę dośrodkową. Siła ta ma postać:

\[ F_d = m \cdot \frac{v^2}{r} \]

W ruchu orbitalnym prędkość \( v \) można wyrazić jako \( v = \frac{2\pi r}{T} \), co daje:

\[ F_d = m \cdot \frac{\left( \frac{2\pi r}{T} \right)^2}{r} = \frac{4\pi^2 m r}{T^2} \]

Z trzeciego Prawa Keplera \( \frac{T^2}{r^3} = \text{const} \), więc \( T^2 \propto r^3 \). Podstawiając to, otrzymujemy zależność siły od odległości:

\[ F \propto \frac{1}{r^2} \]

Siła grawitacji musi również zależeć od mas ciał, ponieważ większe masy oznaczają silniejsze przyciąganie. Dlatego siła jest proporcjonalna do iloczynu obu mas:

\[ F \propto \frac{m_1 \cdot m_2}{r^2} \]

Dodając stałą proporcjonalności \( G \), wyznaczoną doświadczalnie przez Henry'ego Cavendisha, otrzymujemy wzór:

\[ F = G \cdot \frac{m_1 \cdot m_2}{r^2} \]

Stała grawitacji \( G \) wynosi \( 6,674 \cdot 10^{-11} \ \text{N} \cdot \text{m}^2 / \text{kg}^2 \).

3. Prawo Powszechnej Grawitacji

Newton sformułował Prawo Powszechnej Grawitacji, które opisuje uniwersalną siłę przyciągania między dwoma ciałami. Zgodnie z tym prawem, każde dwa ciała w przestrzeni, posiadające masę, przyciągają się wzajemnie z siłą proporcjonalną do iloczynu ich mas i odwrotnie proporcjonalną do kwadratu odległości między nimi:

\[ F_g = G \cdot \frac{m_1 m_2}{r^2} \]

gdzie:

\( G \) – stała grawitacji, \( G = 6,674 \times 10^{-11} \ \text{N} \cdot \text{m}^2 / \text{kg}^2 \),
\( m_1, m_2 \) – masy ciał,
\( r \) – odległość między środkami mas tych ciał.

To prawo wyjaśnia, dlaczego planety krążą wokół Słońca, dlaczego Księżyc utrzymuje się na orbicie wokół Ziemi, oraz dlaczego ciała spadają na powierzchnię Ziemi. Jest to siła działająca na każdą masę we Wszechświecie, niezależnie od jej położenia.

Warto podkreślić, że siła grawitacji działa w sposób wzajemny: Ziemia przyciąga Księżyc z tą samą siłą, z jaką Księżyc przyciąga Ziemię. Jednak te siły nie równoważą się (ponieważ każda działa na inne ciało). To właśnie wzajemne przyciąganie odpowiada za obserwowany ruch orbitalny.

Siła grawitacji staje się coraz mniejsza w miarę zwiększania odległości między ciałami, co oznacza, że oddziaływanie grawitacyjne planet w odległych układach jest znacznie słabsze. Jednak nawet przy bardzo dużych odległościach grawitacja nigdy nie znika całkowicie – jej zasięg jest nieskończony, choć intensywność maleje asymptotycznie.

4. Przykład Zadania: Równowaga Sił Grawitacji Ziemi i Słońca

Przykład: Gdzie należy umieścić człowieka (w jakiej odległości od powierzchni Ziemi), aby siła grawitacji Ziemi została zrównoważona przez siłę grawitacji Słońca? Przyjmujemy:

Masa Ziemi: \( M_\text{Z} = 5,972 \times 10^{24} \, \text{kg} \)
Masa Słońca: \( M_\text{S} = 1,989 \times 10^{30} \, \text{kg} \)
Masa człowieka: \( m = 70 \, \text{kg} \)
Odległość Ziemia-Słońce: \( R = 1,496 \times 10^{11} \, \text{m} \)
Promień Ziemi: \( R_\text{Z} = 6,371 \times 10^{6} \, \text{m} \)
Stała grawitacji: \( G = 6,674 \times 10^{-11} \, \text{m}^3\text{kg}^{-1}\text{s}^{-2} \)

Pokaż rozwiązanie krok po kroku

Rozwiązanie:

Krok 1: Zapisujemy równanie równowagi sił grawitacyjnych działających na człowieka:

\[ \frac{G M_\text{Z} m}{(R_\text{Z} + h)^2} = \frac{G M_\text{S} m}{(R - (R_\text{Z} + h))^2} \]

Gdzie:

\( m \): masa człowieka,
\( h \): wysokość nad powierzchnią Ziemi,
\( R_\text{Z} + h \): odległość człowieka od środka Ziemi,
\( R - (R_\text{Z} + h) \): odległość człowieka od środka Słońca.

Krok 2: Upraszczamy równanie, usuwając masę człowieka \( m \) (działa po obu stronach równania):

\[ \frac{G M_\text{Z}}{(R_\text{Z} + h)^2} = \frac{G M_\text{S}}{(R - (R_\text{Z} + h))^2} \]

Krok 3: Upraszczamy równanie jeszcze bardziej, eliminując \( G \):

\[ \frac{M_\text{Z}}{(R_\text{Z} + h)^2} = \frac{M_\text{S}}{(R - (R_\text{Z} + h))^2} \]

Krok 4: Wprowadzamy zmienną pomocniczą \( x = R_\text{Z} + h \), gdzie:

\( x \): odległość człowieka od środka Ziemi,
\( R - x \): odległość człowieka od środka Słońca.

Po podstawieniu równanie przyjmuje postać:

\[ \frac{M_\text{Z}}{x^2} = \frac{M_\text{S}}{(R - x)^2} \]

Krok 5: Przekształcamy równanie, aby znaleźć \( x \). Po rozwiązaniu równania numerycznie dla podanych danych:

\( x \approx 6,631 \times 10^6 \, \text{m} \)

Obliczamy wysokość \( h \) nad powierzchnią Ziemi:

\[ h = x - R_\text{Z} \approx 6,631 \times 10^6 - 6,371 \times 10^6 = 259 \, \text{km} \]

Odpowiedź: Człowiek powinien znajdować się około \( 259 \, \text{km} \) nad powierzchnią Ziemi, aby siły grawitacji Ziemi i Słońca były w równowadze.

5. Skutki i Zastosowania

1. Orbity planet

Prawo Powszechnej Grawitacji wyjaśnia eliptyczne orbity planet oraz mechanizm ich ruchu wokół gwiazd, zgodny z prawami Keplera.

2. Tides (Pływy)

Oddziaływanie grawitacyjne między Ziemią a Księżycem wywołuje pływy morskie, które wpływają na dynamikę oceanów.

3. Loty kosmiczne

Projektowanie trajektorii sond kosmicznych wymaga uwzględnienia przyciągania grawitacyjnego Ziemi, Słońca i innych planet.

4. Odkrycia w astronomii

Analiza odchyleń ruchów ciał niebieskich umożliwiła odkrycie planet takich jak Neptun, a także badanie czarnych dziur i ciemnej materii.

Fizyka Fascynuje