1. Wstęp do Energii Mechanicznej
Energia mechaniczna to suma energii kinetycznej i potencjalnej, która opisuje zdolność układu do wykonania pracy. W układach fizycznych energia może być przekazywana między obiektami za pomocą sił wewnętrznych i zewnętrznych.
W układzie izolowanym, w którym działają tylko siły wewnętrzne, całkowita energia mechaniczna pozostaje stała. Natomiast gdy na układ działają siły zewnętrzne, możliwa jest zmiana energii mechanicznej. Ta zmiana jest wynikiem pracy wykonanej przez siłę zewnętrzną, co wyraża się równaniem:
Gdy praca siły zewnętrznej jest dodatnia, energia mechaniczna układu wzrasta; gdy jest ujemna, energia mechaniczna maleje.
2. Energia Kinetyczna
Energia kinetyczna \( E_k \) to energia związana z ruchem ciała o masie \( m \) i prędkości \( v \). Aby wyprowadzić wzór na energię kinetyczną, analizujemy pracę potrzebną do rozpędzenia ciała od prędkości \( 0 \) do \( v \).
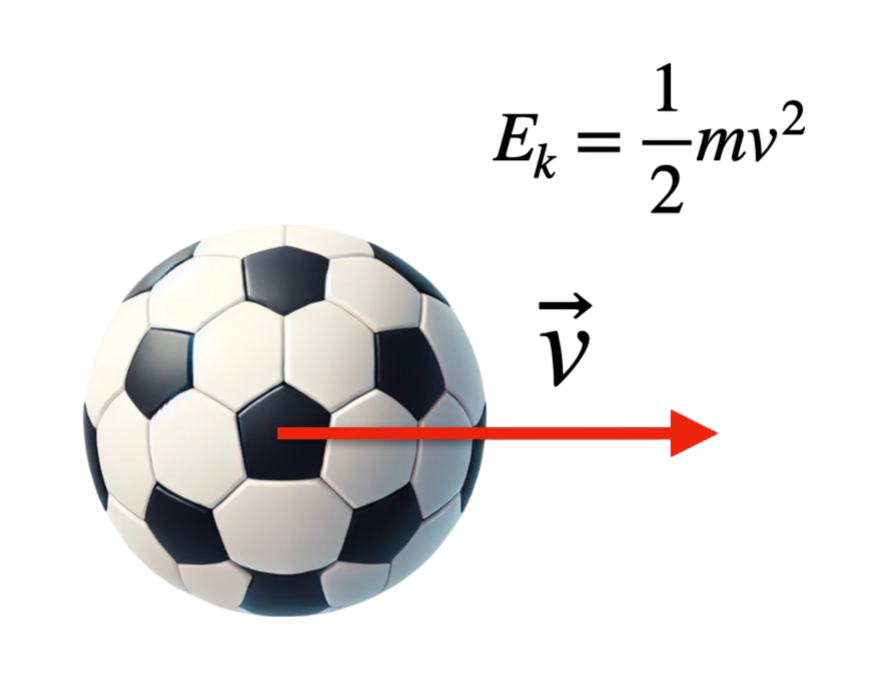
Praca wykonana przez siłę przyspieszającą ciało wynosi:
Korzystając z drugiej zasady dynamiki Newtona (\( F = ma \)) i podstawiając przyspieszenie jako \( a = \frac{v^2}{2s} \), otrzymujemy:
Ostatecznie wzór na energię kinetyczną ma postać:
Przykłady: Energia kinetyczna samochodu, energia kinetyczna piłki po rzucie.
3. Energia Potencjalna
Energia potencjalna \( E_p \) związana jest z położeniem ciała w polu grawitacyjnym. Dla ciała o masie \( m \) podniesionego na wysokość \( h \) nad powierzchnią Ziemi wyrażamy ją wzorem:
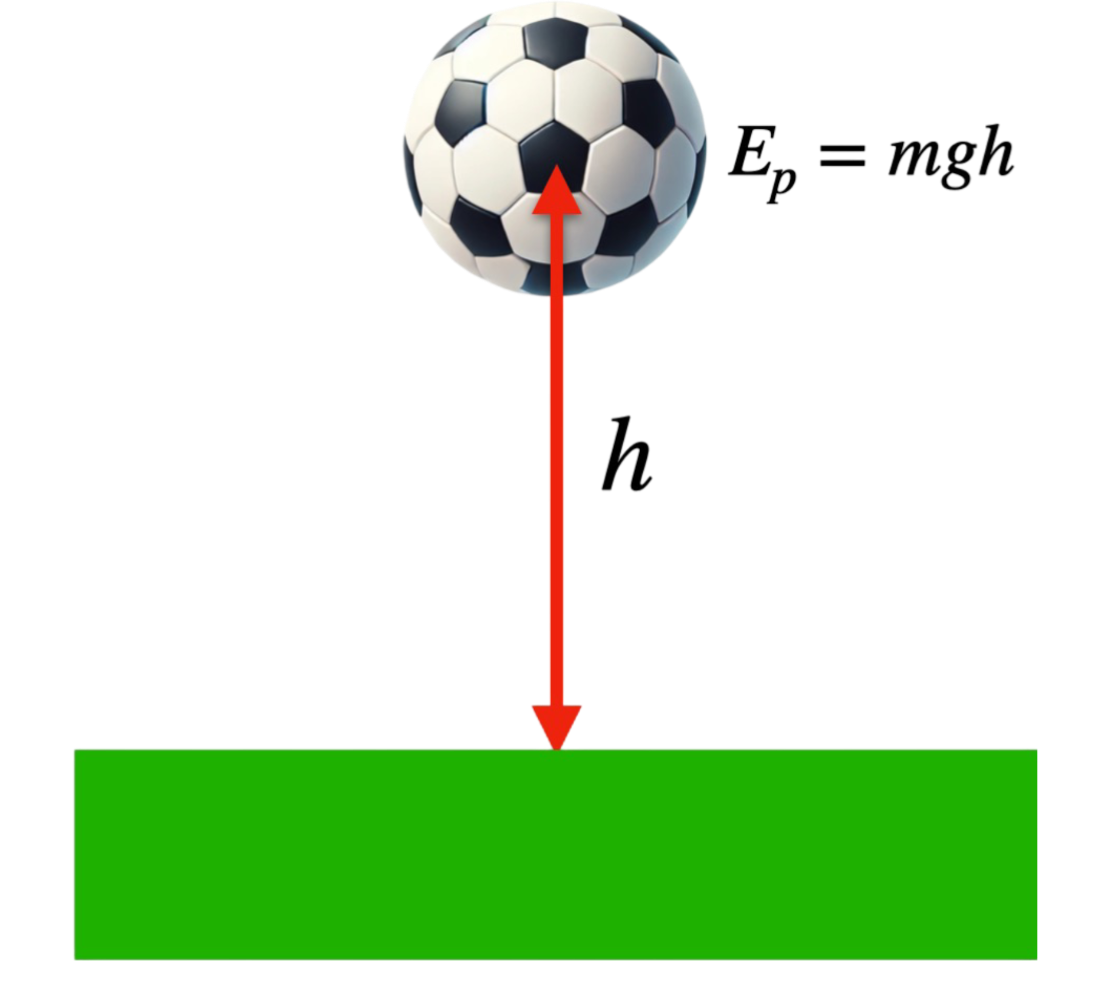
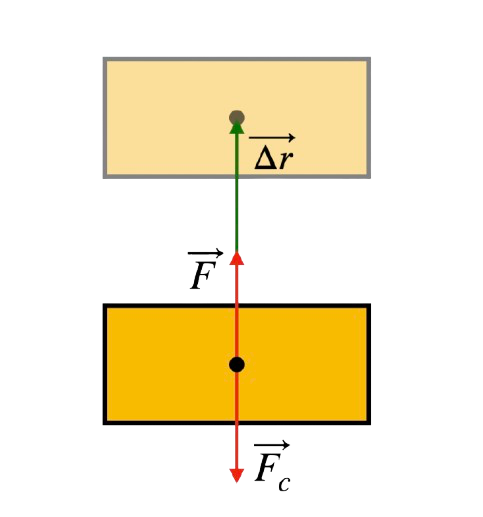
Aby wyprowadzić wzór na energię potencjalną grawitacyjną, analizujemy pracę potrzebną do podniesienia ciała na wysokość \( h \):
Zauważamy że siła \(F\), co do wartościi jest równa \(F_c\). Z kolei \(\Delta r\) to nic innego jak nasze \(h\). Podstawiamy i otrzymujemy:
Stąd energia potencjalna wynosi:
Przykłady: Energia potencjalna wody w zbiorniku, energia podniesionego kamienia.
4. Energia Potencjalna Sprężystości
Energia potencjalna sprężystości \( E_s \) jest energią zmagazynowaną w ciałach sprężystych, takich jak sprężyny, w wyniku ich rozciągania lub ściskania.
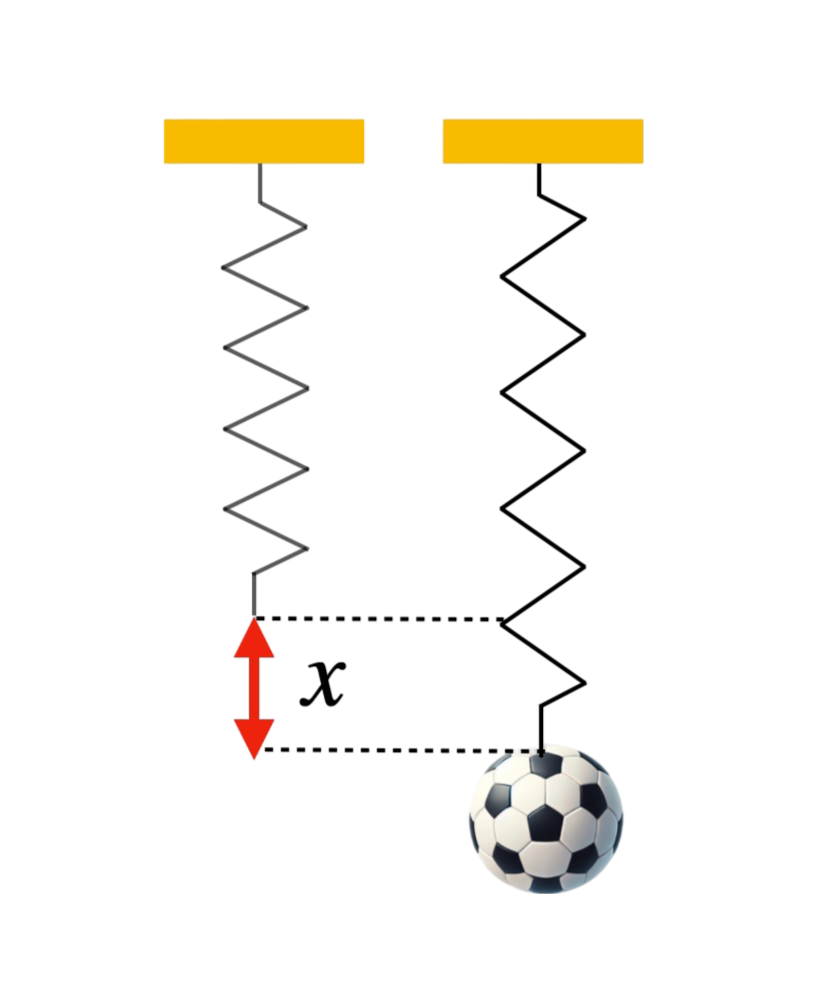
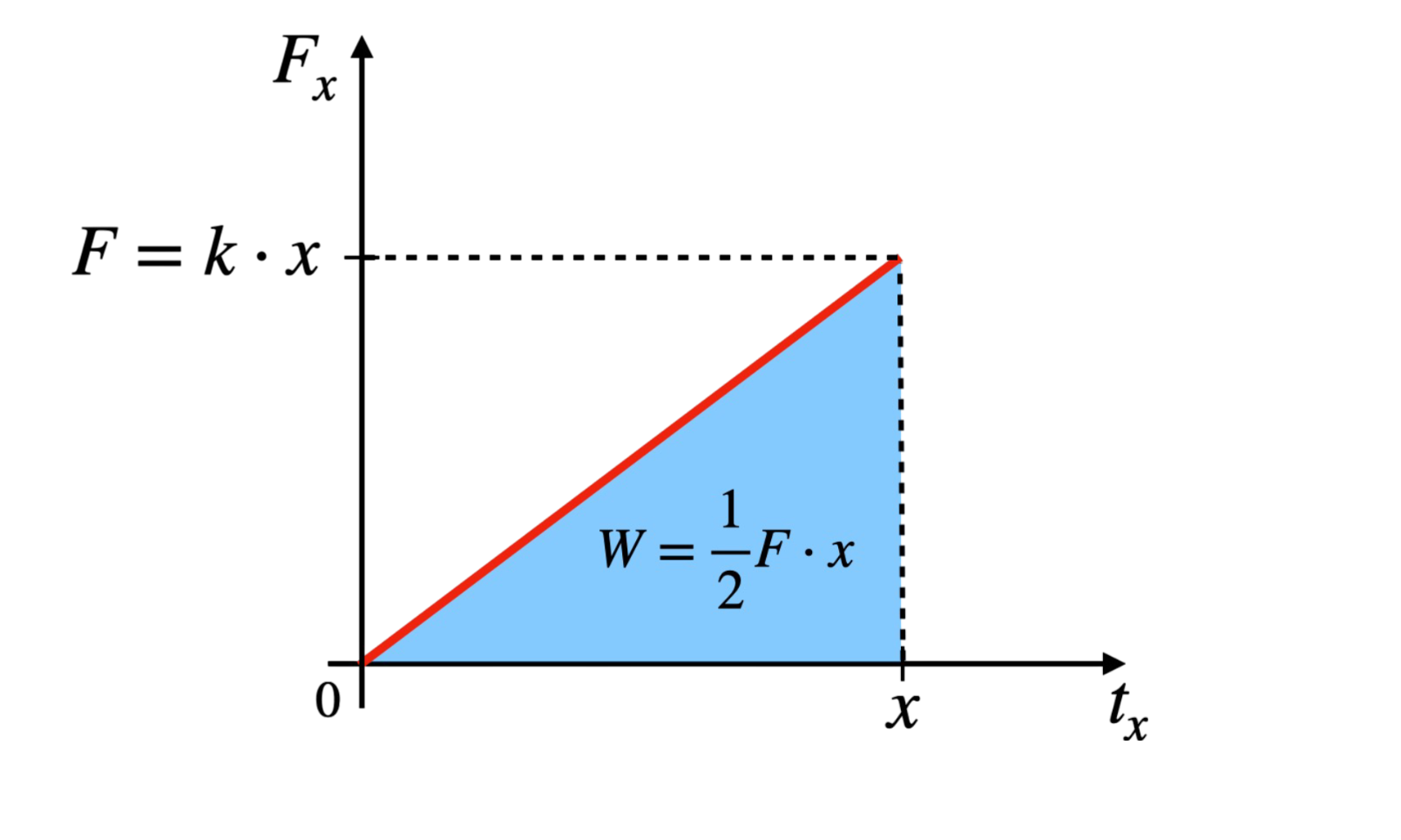
Wyprowadzenie wzoru na energię potencjalną sprężystości opiera się na analizie pracy wykonanej podczas rozciągania sprężyny o współczynniku sprężystości \( k \) na odległość \( x \):
Siła \(F\) potrzebna do naciągnięcia sprężyny o długość \(x\):
Stąd praca wykonana podczas rozciągania wynosi (Pole trójkąta pod wykresem):
Praca wykonana nad ciałem = Energia dostarczona ciału, więc:
Przykłady: Energia sprężyny, energia napiętej gumki.
5. Podsumowanie
Energia mechaniczna to suma energii kinetycznej, związanej z ruchem obiektu, oraz energii potencjalnej, wynikającej z jego położenia lub oddziaływań sił. W układach izolowanych pozostaje stała, podczas gdy w układach otwartych może się zmieniać w wyniku pracy sił zewnętrznych.