Spis treści
Równia Pochyła
Równia pochyła to powierzchnia nachylona pod kątem do poziomu, umożliwiająca analizę ruchu ciał pod wpływem siły grawitacji oraz sił oporowych, takich jak tarcie. Omówimy dwa przypadki: ciało poruszające się po równi bez tarcia oraz ciało z uwzględnieniem siły tarcia.
1. Równia Pochyła bez Tarcia
Rozważmy ciało o masie \( m \), które znajduje się na równi nachylonej pod kątem \( \alpha \). Jeśli powierzchnia równi jest idealnie gładka, nie występuje siła tarcia, więc ruch ciała jest zależny wyłącznie od składowych siły ciężkości.
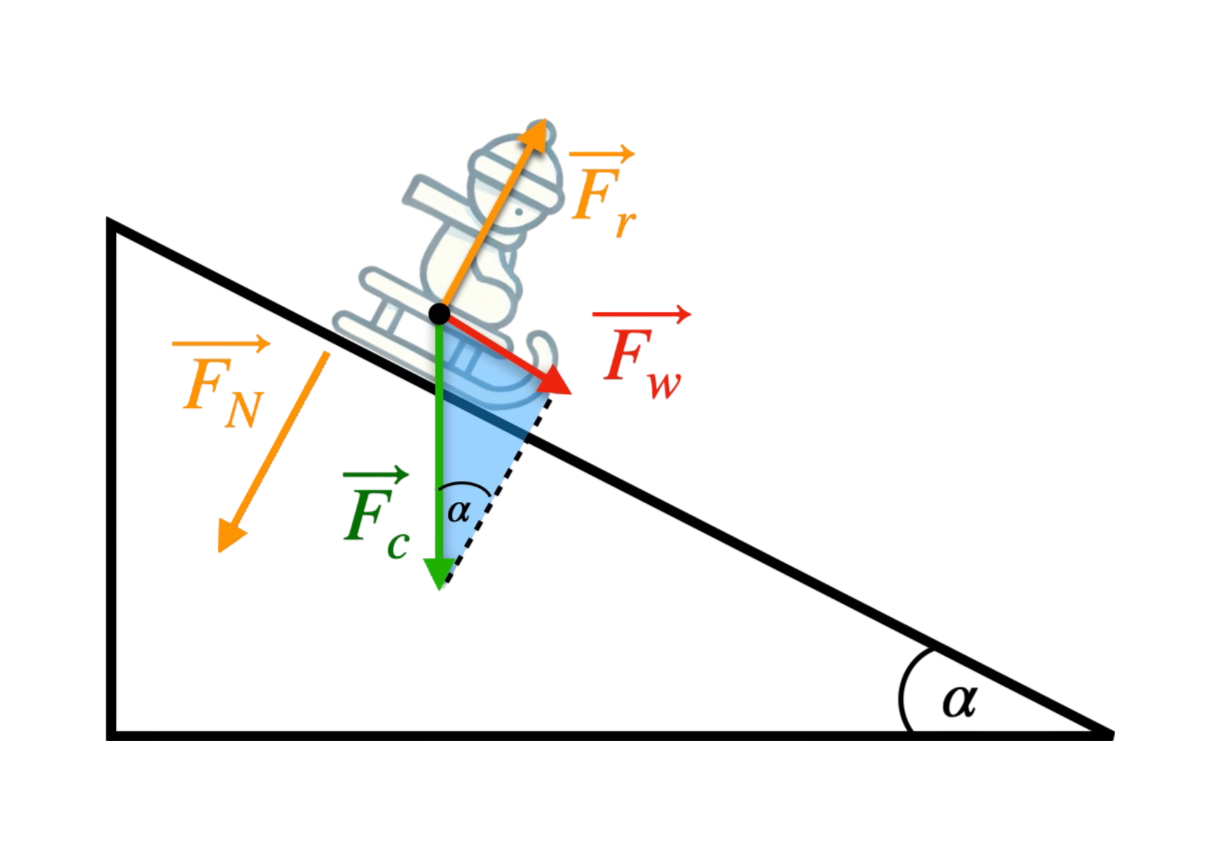
Siły działające na ciało:
-
Siła ciężkości \( \vec{F_g} = m \cdot g \) —
można ją rozłożyć na dwie składowe:
- Składowa równoległa \( F_{\parallel} = m \cdot g \cdot \sin(\alpha) \) — powoduje ruch ciała w dół równi.
- Składowa prostopadła \( F_{\perp} = m \cdot g \cdot \cos(\alpha) \) — jest równoważona przez reakcję podłoża.
- Siła reakcji podłoża \( \vec{F_r} \) — działa prostopadle do powierzchni równi i równoważy składową prostopadłą siły ciężkości \( F_{\perp} \).
Ruch ciała po równi wywołuje jedynie składowa równoległa siły ciężkości, co prowadzi do powstania przyspieszenia. Wartość przyspieszenia ciała wyrażona jest wzorem:
Przeanalizujmy krok po kroku wyprowadzenie wzoru na przyspieszenie ciała poruszającego się po równi pochyłej, zaczynając od drugiego prawa dynamiki Newtona:
- Na ciało działa siła ciężkości \( \vec{F_g} = m \cdot g \), którą rozkładamy na dwie składowe:
- Składowa równoległa: \( F_{\parallel} = m \cdot g \cdot \sin(\alpha) \), odpowiadająca za ruch ciała w dół równi.
- Składowa prostopadła: \( F_{\perp} = m \cdot g \cdot \cos(\alpha) \), która jest równoważona przez siłę reakcji podłoża \( \vec{F_r} \).
- Stosując drugie prawo Newtona wzdłuż kierunku równi (wzdłuż składowej równoległej):
- Podstawiając \( F_{\text{wyp}} = F_{\parallel} \):
- Dzieląc obie strony przez \( m \), otrzymujemy przyspieszenie:
Wynikowy wzór pokazuje, że przyspieszenie ciała na równi pochyłej bez tarcia zależy jedynie od kąta nachylenia \( \alpha \) i przyspieszenia ziemskiego \( g \).
Przykład: Dla równi nachylonej pod kątem 30° i ciała o masie 5 kg, przyspieszenie wynosi \( a = 9.81 \cdot \sin(30^\circ) = 4.905 \, \text{m/s}^2 \).
2. Równia Pochyła z Tarciem
Teraz rozważmy przypadek, gdy między ciałem a powierzchnią równi występuje tarcie. Siła tarcia działa przeciwnie do kierunku ruchu, zmniejszając przyspieszenie ciała.
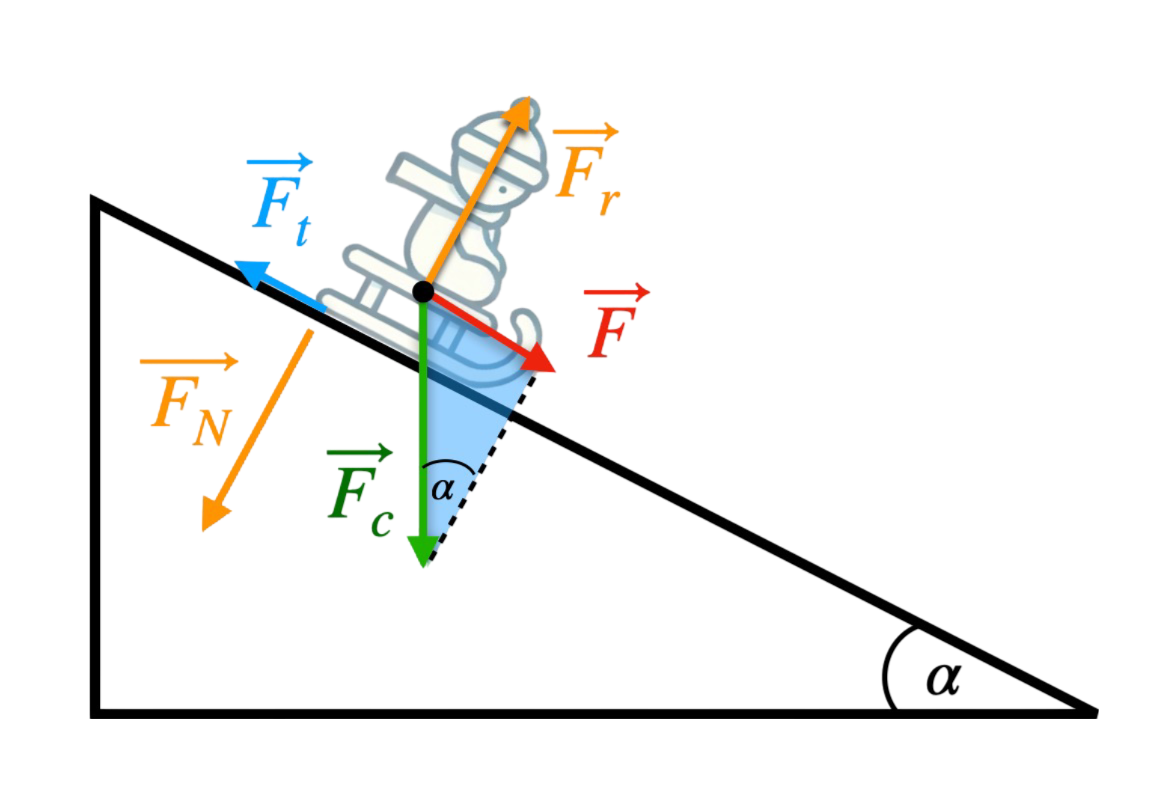
Siły działające na ciało:
- Siła ciężkości \( \vec{F_g} = m \cdot g \) — tak jak wcześniej, rozkłada się na składowe równoległą i prostopadłą.
- Siła reakcji podłoża \( \vec{F_r} \) — równoważy składową prostopadłą \( F_{\perp} \).
- Siła tarcia \( \vec{F_t} = \mu \cdot F_N \) — siła tarcia zależy od współczynnika tarcia \( \mu \) oraz siły nacisku na podłoże \( F_N \).
Przyspieszenie ciała wynika z siły równoległej siły ciężkości, pomniejszonej o siłę tarcia. Wzór na przyspieszenie w przypadku występowania tarcia ma postać:
Rozważmy przypadek, gdy występuje siła tarcia, która przeciwdziała ruchowi. Wykorzystamy drugi zasadę dynamiki Newtona:
- Na ciało działa siła tarcia \( F_t = \mu \cdot F_N = \mu \cdot m \cdot g \cdot \cos(\alpha) \), gdzie \( \mu \) to współczynnik tarcia.
- Wypadkowa siła działająca wzdłuż równi pochyłej wynosi:
- Podstawiając \( F_{\parallel} = m \cdot g \cdot \sin(\alpha) \) i \( F_t = \mu \cdot m \cdot g \cdot \cos(\alpha) \):
- Stosując drugie prawo dynamiki Newtona, \( F_{\text{wyp}} = m \cdot a \):
- Dzieląc obie strony przez \( m \), otrzymujemy wzór na przyspieszenie z uwzględnieniem tarcia:
Ten wzór pokazuje, że przyspieszenie jest mniejsze niż w przypadku równi bez tarcia, ze względu na siłę tarcia działającą przeciwnie do ruchu.
Przykład: Dla równi nachylonej pod kątem 30°, ciała o masie 5 kg oraz współczynnika tarcia \( \mu = 0.2 \), przyspieszenie wynosi \( a = 9.81 \cdot \sin(30^\circ) - 0.2 \cdot 9.81 \cdot \cos(30^\circ) \approx 2.45 \, \text{m/s}^2 \).
3. Przykłady Zastosowań Równi Pochyłej
Równia pochyła znajduje szerokie zastosowanie zarówno w technice, jak i w życiu codziennym. Przykłady użycia równi pochyłej:
- Rampy: Rampy ułatwiają przemieszczanie ciężkich przedmiotów, gdyż pozwalają na zmniejszenie siły potrzebnej do ich podniesienia.
- Układy transportowe: W przemyśle i kopalniach równia jest wykorzystywana do przesuwania materiałów wzdłuż pochylonych powierzchni.
- Pojazdy na zboczach: Równia pochyła jest używana do analizy dynamiki pojazdów na wzniesieniach i zjazdach, pomagając określić siłę napędową i przyczepność.