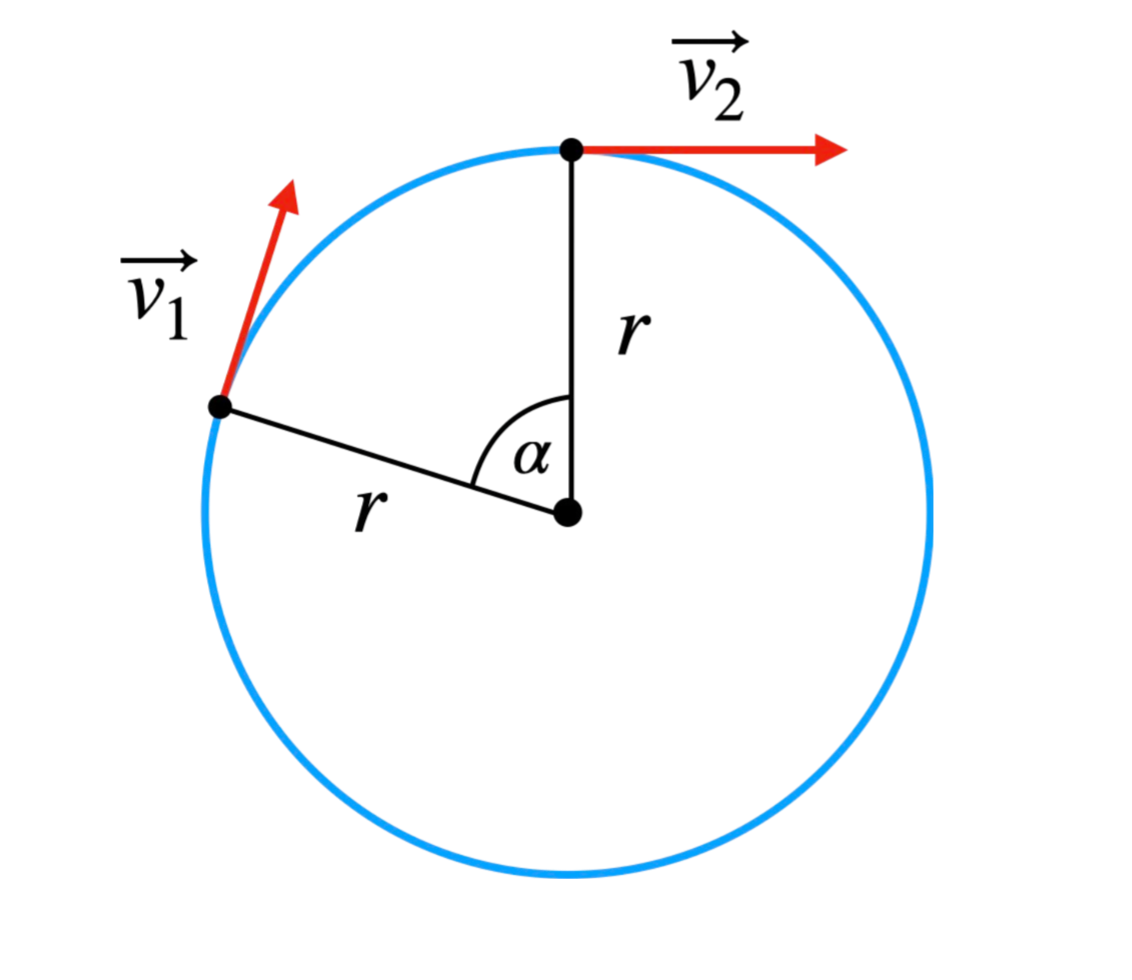
1. Miara Łukowa
Miara łukowa pozwala opisywać kąt jako stosunek długości łuku \( s \) do promienia \( r \) okręgu, co wyraża się wzorem:
Dzięki temu możemy wyrazić kąty w radianach, gdzie pełny obrót odpowiada wartości \( 2\pi \) radianów. Miara łukowa jest szczególnie przydatna w analizie ruchu po okręgu.

Przykłady: \( 2\pi =360^\circ\), \( \pi =180^\circ\), \( \frac{\pi}{2} =90^\circ\), \( \frac{\pi}{4} =45^\circ\).
2. Okres i Częstotliwość
Okres (oznaczany jako \( T \)) to czas potrzebny na wykonanie pełnego obrotu, mierzonego w sekundach [s]. W ruchu po okręgu częściej używamy pojęcia częstotliwości.
Częstotliwość (oznaczana jako \( f \)) to liczba pełnych obrotów na sekundę, wyrażona w hercach [Hz].
I jest odwrotnością okresu:
3. Szybkość Kątowa
Szybkość kątowa \( \omega \) opisuje, jak szybko ciało przemieszcza się po okręgu, mierzona w radianach na sekundę [rad/s]. Definiuje się ją jako kąt \( \alpha \) przebywany w jednostce czasu:
Wiemy już, że w czasie \(T\) (okres), ciało wykonuje pełny obrót. Pełny obrót w miarze łukowej to \( 2\pi\) (radianów). Podstawiając; \(\alpha = 2\pi\) i \(t = T\) do powyższego wzoru, otrzymujemy:
Oznacza to, że szybkość kątowa zależy od okresu obiegu \( T \) i pozwala na łatwe określenie prędkości przy ruchu po okręgu o dowolnym promieniu.
4. Szybkość w Ruchu Po Okręgu
Ciało pokonuje drogę równą długości obwodu koła - \( 2\pi r\) w czasie \(T\). Szybkość \( v \) ciała poruszającego się po okręgu o promieniu \( r \) oraz okresie \( T \) wyraża się więc wzorem:
Możemy do tego wzoru podstawić znaną nam zależność, że \( \omega = \frac{2 \pi}{T} \) i otrzymujemy:
wzory te oznaczają, że szybkość zależy od całkowitej długości okręgu \( 2 \pi r \) i czasu \( T \) potrzebnego na jego pokonanie. Wartość \( v \) pozostaje stała przy jednostajnym ruchu po okręgu.
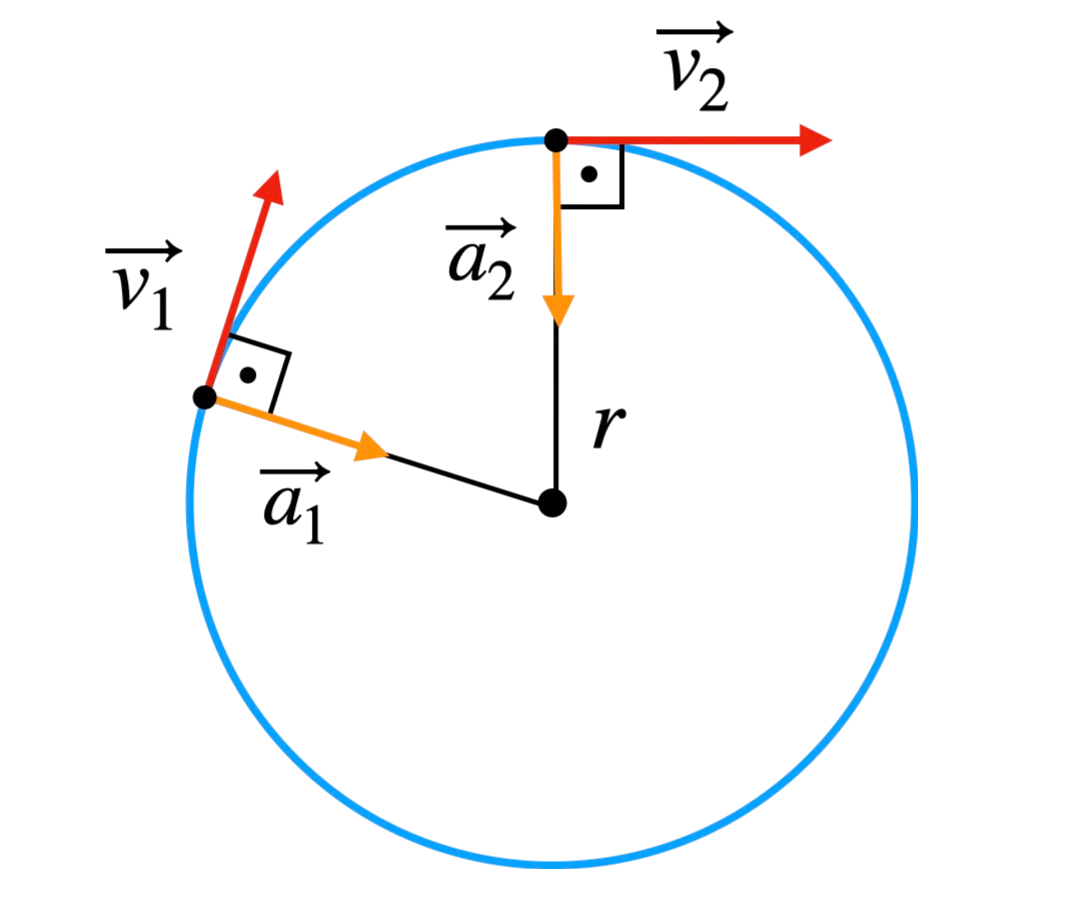
5. Przyspieszenie Dośrodkowe
Przyspieszenie dośrodkowe \( a_c \) działa w kierunku środka okręgu i wyrażane jest wzorem:
Przyspieszenie to utrzymuje ciało w ruchu po okręgu, stale zmieniając kierunek prędkości bez zmiany jej wartości. Zależność \( a_c = \omega^2 r \) pokazuje, że siła dośrodkowa zależy od promienia okręgu oraz szybkości kątowej \( \omega \).