Prawo Ohma

1. Wstęp

Prawo Ohma to jedna z podstawowych zasad fizyki, opisująca zależność między napięciem, natężeniem prądu i oporem elektrycznym w przewodnikach. Dzięki swojej prostocie i uniwersalności jest ono kluczowe w analizie i projektowaniu obwodów elektrycznych.

Podstawowy wzór Prawa Ohma wyraża tę zależność jako:

gdzie: \( U \) - napięcie (w woltach, \( V \)), \( I \) - natężenie prądu (w amperach, \( A \)), \( R \) - opór elektryczny (w omach, \( \Omega \)).

Prawo to opisuje, jak zmiana jednej z tych wielkości wpływa na pozostałe. Przykładowo, wzrost napięcia powoduje wzrost natężenia prądu, jeśli opór pozostaje stały. Dzięki temu prawo Ohma jest szeroko stosowane w analizie obwodów, od prostych przewodników po bardziej złożone układy elektryczne.

2. Siła Elektromotoryczna

Siła elektromotoryczna (\( \mathcal{E} \)) to praca wykonana przez źródło napięcia nad jednostkowym ładunkiem, aby przepchnąć go przez cały obwód. Definiujemy ją jako:

Gdzie: \( W \) - praca wykonana nad ładunkiem (w dżulach, \( J \)), \( \Delta q \) - ładunek elektryczny (w kulombach, \( C \)).

W prostym języku siła elektromotoryczna to "potencjał", który popycha elektrony przez obwód, tworząc prąd. Można to sobie wyobrazić jako pompę, która "podbija" wodę do góry w układzie hydraulicznym.

3. Wyprowadzenie Prawa Ohma dla Całego Obwodu

Zakładamy, że w obwodzie znajduje się tylko jeden przewodnik (np. rezystor), a siła elektromotoryczna \( \mathcal{E} \) działa dzięki reakcjom chemicznym zachodzącym w źródle napięcia (np. w baterii). Praca wykonana przez siłę elektromotoryczną, określona jako \( \mathcal{E} \cdot \Delta q \), zostanie całkowicie zamieniona na energię wewnętrzną rezystora, co oznacza, że cała energia jest rozpraszana w postaci ciepła Joule’a. Zakładamy brak strat w przewodach doprowadzających, czyli cała energia jest przekształcana w ciepło w rezystorze.

Wzór opisujący energię rozpraszaną w rezystorze wynika z prawa Joule’a (jeżeli nie pamiętasz, wróć do poprzedniego tematu):

gdzie: \( W \) - energia rozproszona w rezystorze, \( I \) - prąd płynący w obwodzie, \( R \) - opór rezystora, \( \Delta t \) - czas przepływu prądu.

Jednocześnie energia dostarczona przez źródło napięcia jest wyrażona jako:

Korzystając z definicji prądu \( I = \frac{\Delta q}{\Delta t} \), możemy uprościć to wyrażenie do postaci:

Ostatecznie otrzymujemy wyrażenie na prąd płynący w obwodzie:

4. Prawo Ohma z Uwzględnieniem Oporu Wewnętrznego

W rzeczywistości źródła napięcia, takie jak baterie, mają swój własny opór wewnętrzny \( r \). W takim przypadku musimy uwzględnić dwie składowe energii: \( Q_1 \) - energia zamieniona na ciepło w oporze zewnętrznym \( R \), \( Q_2 \) - energia zamieniona na ciepło w oporze wewnętrznym \( r \).

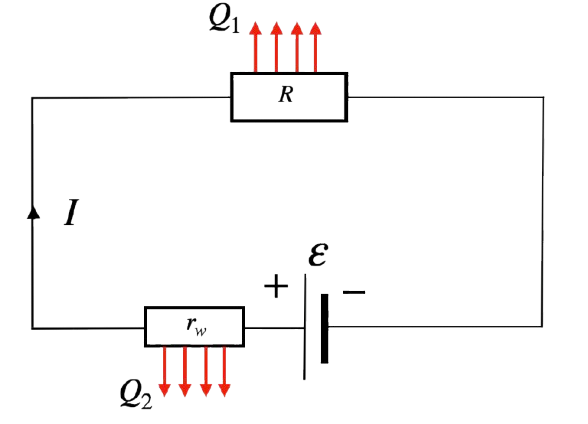
Po podstawieniu odpowiednich wartości mamy:

Upraszczając wyrażenie:

Ostateczna postać prawa Ohma dla obwodu z oporem wewnętrznym wygląda następująco:

Z tego wynika, że całkowity opór obwodu to suma oporu zewnętrznego i oporu wewnętrznego źródła.

5. Przykład Zadania

Zadanie: W obwodzie bateria ma siłę elektromotoryczną \( \mathcal{E} = 12 \, V \), opór zewnętrzny wynosi \( R = 6 \, \Omega \), a opór wewnętrzny baterii to \( r = 2 \, \Omega \). Oblicz natężenie prądu w obwodzie.

Pokaż rozwiązanie krok po kroku