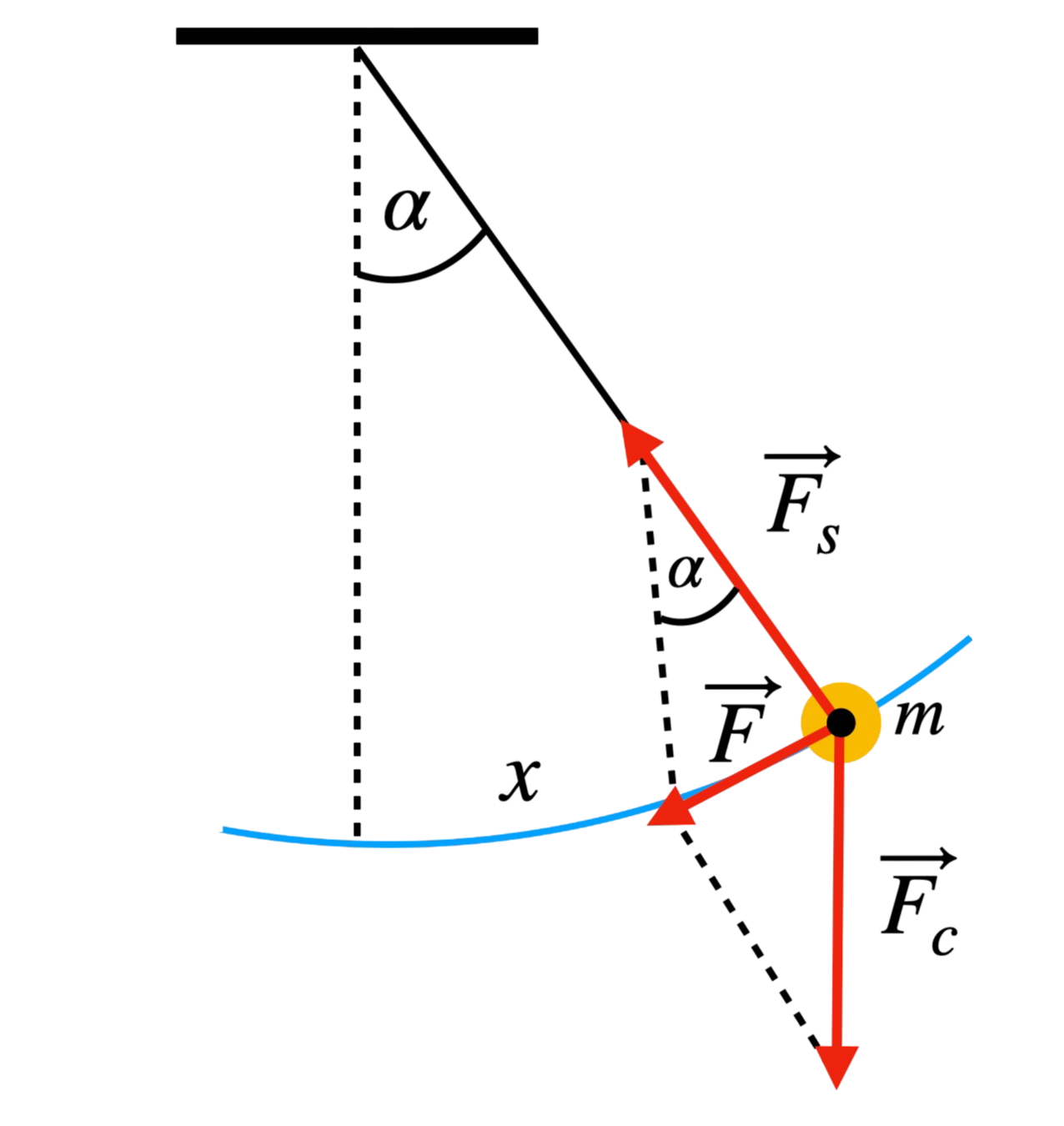
Wahadło Matematyczne
Wahadło matematyczne to uproszczony model fizyczny, w którym punktowa masa \( m \) zawieszona jest na cienkiej, nierozciągliwej nici o długości \( l \). Ruch takiego wahadła opisuje drgania harmoniczne i oscylacje w granicach małych kątów wychylenia, zazwyczaj dla \( \alpha\) mniejszej niż \(\approx 7^\circ \).
W prawdziwym życiu wahadłem matematycznym może być ciężka kulka zawieszona na cienkiej nici, która jest jak najmniej rozciągliwa i nierozciągająca się. Model ten jest idealizacją, ponieważ w rzeczywistości występują straty energii, opór powietrza i elastyczność nici.
1. Ruch Wahadła - Analiza
Wahadło matematyczne to przykład układu oscylacyjnego, w którym masa punktowa porusza się pod wpływem siły przywracającej do położenia równowagi. Wyprowadźmy wzór na okres drgań \( T \) przy założeniu, że kąt wychylenia \( \alpha \) jest mały.
Wzór na okres drgań wahadła o długości \(l\), wyrażony jest jako:
2. Doświadczenie - Wyznaczanie Przyśpieszenia ziemskiego
Zadanie 1: Obliczenie częstotliwości drgań wahadła
Oblicz częstotliwość drgań wahadła matematycznego o długości \( l = 1 \, \text{m} \) na Ziemi. Przyspieszenie ziemskie \( g = 9.81 \, \text{m/s}^2 \).
Aby obliczyć częstotliwość drgań wahadła, używamy wzoru na okres drgań wahadła matematycznego:
Częstotliwość \( f \) jest odwrotnością okresu:
Podstawiając wartości: \( l = 1 \, \text{m} \) i \( g = 9.81 \, \text{m/s}^2 \), otrzymujemy:
Odpowiedź: Częstotliwość drgań wahadła wynosi około \( 0.498 \, \text{Hz} \).
Zadanie 2: Długość wahadła na Marsie
Jaką długość musi mieć wahadło na Marsie, aby miało taki sam okres drgań jak wahadło o długości \( l = 1 \, \text{m} \) na Ziemi? Na Marsie przyspieszenie grawitacyjne wynosi \( a_{\text{Mars}} = 3.71 \, \text{m/s}^2 \).
Aby okres drgań wahadła był taki sam, musi być spełniona równość okresów. Wzór na okres drgań wahadła matematycznego jest:
Aby okres drgań na Marsie był taki sam jak na Ziemi, mamy:
Po uproszczeniu otrzymujemy:
Podnosząc do kwadratu obie strony, mamy:
Przekształcamy to do postaci:
Podstawiając wartości: \( l_{\text{Ziemia}} = 1 \, \text{m} \), \( a_{\text{Mars}} = 3.71 \, \text{m/s}^2 \), \( g_{\text{Ziemia}} = 9.81 \, \text{m/s}^2 \), otrzymujemy:
Odpowiedź: Wahadło na Marsie musi mieć długość około \( 0.378 \, \text{m} \), aby miało taki sam okres drgań jak wahadło o długości \( 1 \, \text{m} \) na Ziemi.
3. Przykłady Zastosowań
Wahadło matematyczne jest kluczowym modelem w mechanice, a jego zastosowania obejmują:
- Pomiar czasu: Wahadła były wykorzystywane w zegarach mechanicznych dzięki swojej regularności.
- Eksperymenty w fizyce: Umożliwiają badanie siły ciężkości oraz przyspieszenia ziemskiego \( g \).
- Analiza drgań: Służy jako prosty model drgań w systemach inżynieryjnych.