Wzory astronomia
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Siła Grawitacyjna | \(F_g = \frac{G \cdot m_1 \cdot m_2}{r^2}\) | |
Legenda Wzoru:\(F_g\) - Siła Grawitacyjna \(G\) - Stała Grawitacyjna \(m_1\) - Masa pierwszego ciała \(m_2\) - Masa drugiego ciała \(r\) - Odległość między masami 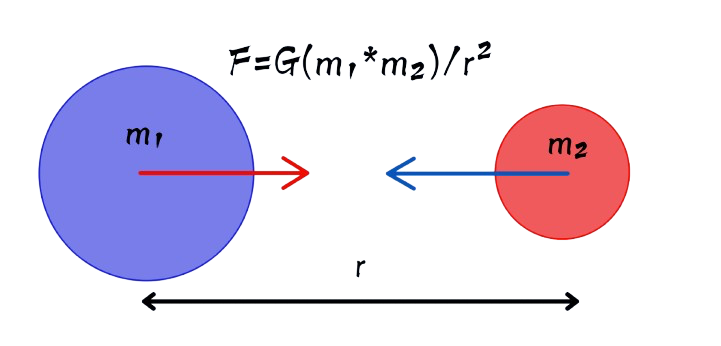
Siła grawitacyjna, z jaką ciało o masie \(m_1\) działa na ciało o masie \(m_2\), jest równa co do wartości, ale przeciwnie skierowana do siły, z jaką ciało \(m_2\) działa na ciało \(m_1\). Mimo że siły te mają tę samą wartość, nie równoważą się, ponieważ działają na różne ciała. |
||
| Pierwsza Prędkość Kosmiczna | \(v_1 = \sqrt{\frac{G \cdot M}{R}}\) | |
Legenda Wzoru:\(v_1\) - Prędkość Orbitalna \(G\) - Stała Grawitacyjna \(M\) - Masa centralnego ciała (na przykład, masa planety) \(R\) - Odległość od środka centralnego ciała do obiektu poruszającego się po orbicie Wyprowadzenie wzoru:Prędkość kosmiczną definiujemy jako minimalną prędkość, którą trzeba nadać ciału, aby utrzymać je na orbicie w określonej wysokości. Korzystając z równania siły grawitacyjnej oraz zasady równowagi sił na orbicie, możemy to wyprowadzić. Równanie siły grawitacyjnej między ciałem o masie \( M \) (np. planeta) a ciałem o masie \( m \) (np. satelita) na odległość \( R \) od środka planety jest dane przez: \[ F_{\text{grav}} = \frac{{G \cdot M \cdot m}}{{R^2}} \] Aby utrzymać się na orbicie ciało potrzebuje siłę, która będzie spełniać rolę siły dośrodkowej - \( F_{\text{dośr}} = \frac{{m \cdot v^2}}{R} \), gdzie \( v \) to prędkość satelity na orbicie o promieniu \( R \). Jedyna siła działająca na satelitę to siła grawitacji. Stąd, zasada równowagi sił na orbicie oznacza: \[ F_{\text{grav}} = F_{\text{dośr}} \] Podstawiając wartości obu sił i rozwiązując równanie dla \( v \), otrzymujemy: \[ \frac{{G \cdot M \cdot m}}{{R^2}} = \frac{{m \cdot v^2}}{R} \] Skoro na orbicie kołowej promień \( R \) równy jest odległości od środka planety do ciała, czyli \( R = R \), możemy to zapisać jako: \[ \frac{{G \cdot M}}{{R^2}} = \frac{{v^2}}{R} \] Dzieląc obustronnie przez \( R \), otrzymujemy: \[ \frac{{G \cdot M}}{{R}} = v^2 \] Wreszcie, pierwiastkując obie strony równania, otrzymujemy wzór na pierwszą prędkość kosmiczną: \[ v = \sqrt{\frac{{G \cdot M}}{{R}}} \] |
||
| Druga Prędkość Kosmiczna | \(v_2 = \sqrt{\frac{2 \cdot G \cdot M}{R}}\) | |
Legenda Wzoru:\(v_2\) - Prędkość Orbitalna \(G\) - Stała Grawitacyjna \(M\) - Masa centralnego ciała (na przykład, masa planety) \(R\) - Odległość od środka centralnego ciała do obiektu poruszającego się po orbicie Wyprowadzenie Wzoru:Aby uddalić ciało do miejsca, w którym pole grawitacyjne jest tak słabe że możemy je zaniedbać, konieczne jest nadanie mu odpowiedniej prędkości. Na początku ciało posiada zarówno energię kinetyczną (dzięki prędkości, jaką mu nadaliśmy), jak i energię potencjalną (związana z polem grawitacyjnym, w którym się znajduje). Naszym celem jest doprowadzenie ciała do stanu, w którym nie posiada ono ani energii kinetycznej, ani potencjalnej (jest tak daleko że w przybliżeniu pole grawitacyjne nie wpływa na to ciało). Zgodnie z zasadą zachowania energii, energia początkowa musi równać się sumie energii końcowej: \[ \frac{m \cdot v^2}{2} - \frac{G \cdot m \cdot M}{R} = 0 \] Dzielimy obustronnie przez \(\frac{m}{2}\), aby wyodrębnić prędkość: \[ v^2 = \frac{2 \cdot G \cdot M}{R} \] Następnie, pierwiastkując obie strony równania, otrzymujemy: \[ v = \sqrt{\frac{2 \cdot G \cdot M}{R}} \] |
||
| Trzecie Prawo Keplera | \(\frac{{T^2}}{{R^3}} = \text{const}\) | |
Legenda Wzoru:\( T \) - Okres obiegu \( R \) - Średnia odległość między ciałami Trzecie Prawo Keplera mówi, że stosunek kwadratu okresu obiegu \(T\) do sześcianu średniej odległości \(R\) między ciałami jest stały dla wszystkich planet w układzie słonecznym. |
||
| Praca Siły Grawitacyjnej w Polu Grawitacyjnym | \( W = G \cdot m_1 \cdot m_2 \cdot \left(\frac{1}{{r_2}} - \frac{1}{{r_1}}\right) \) | |
Legenda Wzoru:\( W \) - Praca wykonana w polu grawitacyjnym \( G \) - Stała grawitacyjna \( m_1 \) i \( m_2 \) - Masy dwóch obiektów \( r_1 \) - Odległość początkowa między środkami mas obiektów \( r_2 \) - Odległość końcowa między środkami mas obiektów 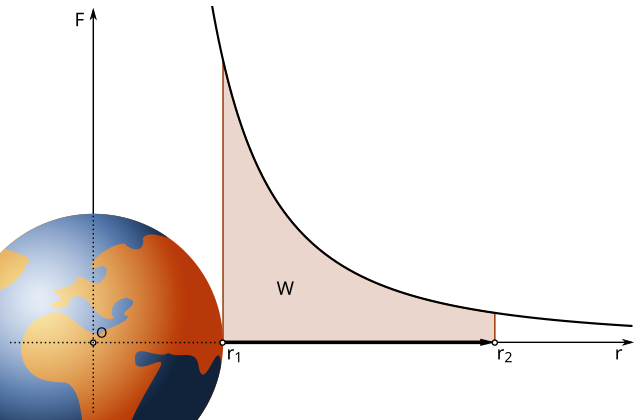
Źródło: MikeRun |
||
| Energia Potencjalna Grawitacji | \( E_p = -\frac{{G \cdot M \cdot m}}{{r}} \) | |
Legenda Wzoru:\( E_p \) - Energia potencjalna grawitacji \( G \) - Stała grawitacyjna \( M \) - Masa ciała centralnego (np. Ziemi) \( m \) - Masa obiektu \( r \) - Odległość od środka masy ciała centralnego |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Siła Grawitacyjna | \(F_g = \frac{G \cdot m_1 \cdot m_2}{r^2}\) |
Legenda Wzoru:\(F_g\) - Siła Grawitacyjna \(G\) - Stała Grawitacyjna \(m_1\) - Masa pierwszego ciała \(m_2\) - Masa drugiego ciała \(r\) - Odległość między masami 
Siła grawitacyjna, z jaką ciało o masie \(m_1\) działa na ciało o masie \(m_2\), jest równa co do wartości, ale przeciwnie skierowana do siły, z jaką ciało \(m_2\) działa na ciało \(m_1\). Mimo że siły te mają tę samą wartość, nie równoważą się, ponieważ działają na różne ciała. |
| Pierwsza Prędkość Kosmiczna | \(v_1 = \sqrt{\frac{G \cdot M}{R}}\) |
Legenda Wzoru:\(v_1\) - Prędkość Orbitalna \(G\) - Stała Grawitacyjna \(M\) - Masa centralnego ciała (np. masa planety) \(R\) - Odległość od środka centralnego ciała do obiektu poruszającego się po orbicie Wyprowadzenie wzoru:Prędkość kosmiczną definiujemy jako minimalną prędkość, którą trzeba nadać ciału, aby utrzymać je na orbicie w określonej wysokości. Korzystając z równania siły grawitacyjnej oraz zasady równowagi sił na orbicie, możemy to wyprowadzić. Równanie siły grawitacyjnej między ciałem o masie \( M \) (np. planeta) a ciałem o masie \( m \) (np. satelita) na odległość \( R \) od środka planety jest dane przez: \[ F_{\text{grav}} = \frac{{G \cdot M \cdot m}}{{R^2}} \] Aby utrzymać się na orbicie ciało potrzebuje siłę, która będzie spełniać rolę siły dośrodkowej - \( F_{\text{dośr}} = \frac{{m \cdot v^2}}{R} \), gdzie \( v \) to prędkość satelity na orbicie o promieniu \( R \). Jedyna siła działająca na satelitę to siła grawitacji. Stąd, zasada równowagi sił na orbicie oznacza: \[ F_{\text{grav}} = F_{\text{dośr}} \] Podstawiając wartości obu sił i rozwiązując równanie dla \( v \), otrzymujemy: \[ \frac{{G \cdot M \cdot m}}{{R^2}} = \frac{{m \cdot v^2}}{R} \] Skoro na orbicie kołowej promień \( R \) równy jest odległości od środka planety do ciała, czyli \( R = R \), możemy to zapisać jako: \[ \frac{{G \cdot M}}{{R^2}} = \frac{{v^2}}{R} \] Dzieląc obustronnie przez \( R \), otrzymujemy: \[ \frac{{G \cdot M}}{{R}} = v^2 \] Wreszcie, pierwiastkując obie strony równania, otrzymujemy wzór na pierwszą prędkość kosmiczną: \[ v = \sqrt{\frac{{G \cdot M}}{{R}}} \] |
| Druga Prędkość Kosmiczna | \(v_2 = \sqrt{\frac{2 \cdot G \cdot M}{R}}\) |
Legenda Wzoru:\(v_2\) - Prędkość Orbitalna \(G\) - Stała Grawitacyjna \(M\) - Masa centralnego ciała (np. masa planety) \(R\) - Odległość od środka centralnego ciała do obiektu poruszającego się po orbicie Wyprowadzenie Wzoru:Aby uddali ciało do miejsca, w którym pole grawitacyjne jest tak słabe że możemy je zaniedbać, konieczne jest nadanie mu odpowiedniej prędkości. Na początku ciało posiada zarówno energię kinetyczną (dzięki prędkości, jaką mu nadaliśmy), jak i energię potencjalną (związana z polem grawitacyjnym, w którym się znajduje). Naszym celem jest doprowadzenie ciała do stanu, w którym nie posiada ono ani energii kinetycznej, ani potencjalnej (jest tak daleko że w przybliżeniu pole grawitacyjne nie wpływa na to ciało). Zgodnie z zasadą zachowania energii, energia początkowa musi równać się sumie energii końcowej: \[ \frac{m \cdot v^2}{2} - \frac{G \cdot m \cdot M}{R} = 0 \] zachowania energii, energia początkowa musi równać się sumie energii końcowej: \[ \frac{m \cdot v^2}{2} - \frac{G \cdot m \cdot M}{R} = 0 \] Dzielimy obustronnie przez \(\frac{m}{2}\), aby wyodrębnić prędkość: \[ v^2 = \frac{2 \cdot G \cdot M}{R} \] Następnie, pierwiastkując obie strony równania, otrzymujemy: \[ v = \sqrt{\frac{2 \cdot G \cdot M}{R}} \] |
| Trzecie Prawo Keplera | \(\frac{{T^2}}{{R^3}} = \text{const}\) |
Legenda Wzoru:\( T \) - Okres obiegu \( R \) - Średnia odległość między ciałami Trzecie Prawo Keplera mówi, że stosunek kwadratu okresu obiegu \(T\) do sześcianu średniej odległości \(R\) między ciałami jest stały dla wszystkich planet w układzie słonecznym. |
| Praca Siły Grawitacyjnej w Polu Grawitacyjnym | \( W = G \cdot m_1 \cdot m_2 \cdot \left(\frac{1}{{r_2}} - \frac{1}{{r_1}}\right) \) |
Legenda Wzoru:\( W \) - Praca wykonana w polu grawitacyjnym \( G \) - Stała grawitacyjna \( m_1 \) i \( m_2 \) - Masy dwóch obiektów \( r_1 \) - Odległość początkowa między środkami mas obiektów \( r_2 \) - Odległość końcowa między środkami mas obiektów 
Źródło: MikeRun |
| Energia Potencjalna Grawitacji | \( E_p = -\frac{{G \cdot M \cdot m}}{{r}} \) |
Legenda Wzoru:\( E_p \) - Energia potencjalna grawitacji \( G \) - Stała grawitacyjna \( M \) - Masa ciała centralnego (np. Ziemi) \( m \) - Masa obiektu \( r \) - Odległość od środka masy ciała centralnego |
Ruch Orbitalny- Animacja:
Quiz - Astronomia
Astronomia
Astronomia jest nauką zajmującą się badaniem ciał niebieskich, takich jak gwiazdy, planety, komety, galaktyki oraz zjawisk i procesów zachodzących we wszechświecie. Skupia się na ich ruchu, składzie chemicznym, pochodzeniu i ewolucji.
Podstawowymi dziedzinami astronomii są astrofizyka, kosmologia, planetologia oraz astrobiologia. Astrofizyka zajmuje się fizycznymi właściwościami ciał niebieskich, kosmologia bada strukturę i ewolucję wszechświata, planetologia koncentruje się na badaniu planet i ich księżyców, a astrobiologia poszukuje życia poza Ziemią.
Astronomia wykorzystuje różnorodne narzędzia obserwacyjne, takie jak teleskopy naziemne i kosmiczne, spektroskopy, radioteleskopy oraz sondy kosmiczne. Dzięki tym narzędziom naukowcy zbierają dane i prowadzą badania mające na celu zrozumienie wszechświata i jego tajemnic.
Badania w astronomii pozwalają na zgłębianie wielu fundamentalnych pytań dotyczących pochodzenia i struktury wszechświata, historii ewolucji gwiazd, powstawania planet, czy też poszukiwania życia w kosmosie. Astronomia ma również istotne znaczenie praktyczne, m.in. w nawigacji kosmicznej, badaniach klimatycznych i poszukiwaniach surowców mineralnych na innych ciałach niebieskich.
Astronomia jest również ściśle związana z fizyką, zwłaszcza poprzez prawa ruchu planetarnego. Prawa Keplera, opracowane przez Johanna Keplera na podstawie obserwacji astronomicznych, opisują ruch planet wokół Słońca. Prawo powszechnego ciążenia, sformułowane przez Isaaca Newtona, wyjaśnia siłę przyciągania między ciałami, która determinuje ruch planet i innych obiektów niebieskich.
Zainteresowanie astronomią jest powszechne wśród ludzi na całym świecie, zarówno wśród naukowców, jak i amatorów obserwujących niebo za pomocą teleskopów amatorskich. Obserwacje astronomiczne dostarczają nie tylko wiedzy naukowej, ale także inspiracji i fascynacji nieznanym.
W skrócie, astronomia jest nauką zajmującą się badaniem wszechświata i jego tajemnic, skupiającą się na ciałach niebieskich i zjawiskach kosmicznych oraz mającą istotne znaczenie zarówno naukowe, jak i kulturowe.