Wzory elektrostatyka
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Najważniejsze | ||
| Prawo Coulomba | \( F = k_e \frac{|q_1 q_2|}{r^2} \) | |
Legenda Wzoru:\( F \) - Siła elektrostatyczna \( k_e \) - Stała elektrostatyczna (\( 8.99 \times 10^9 \, \frac{Nm^2}{C^2} \)) \( q_1, q_2 \) - Ładunki \( r \) - Odległość między ładunkami 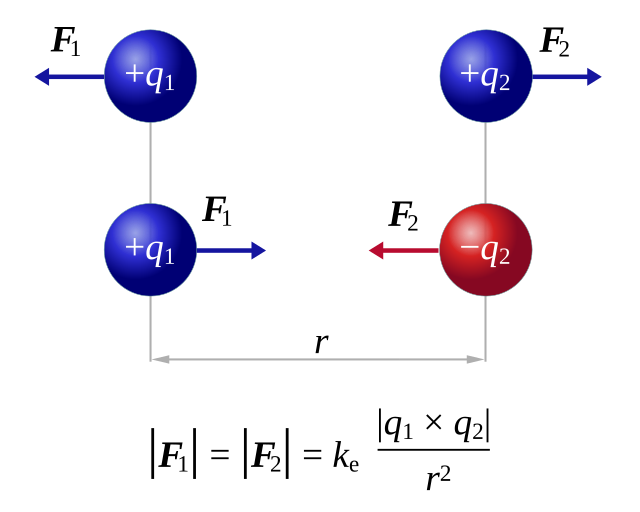
Źródło: Dna-Dennis Opis:
Prawo Coulomba opisuje siłę oddziaływania elektrostatycznego między dwoma ładunkami punktowymi, która jest odwrotnie proporcjonalna do kwadratu odległości między nimi. |
||
| Natężenie pola elektrycznego | \( E = \frac{F}{q} = k_e \frac{|Q|}{r^2} \) | |
Legenda Wzoru:\( E \) - Natężenie pola elektrycznego \( F \) - Siła działająca na ładunek próbny \( q \) \( Q \) - Ładunek źródłowy \( k_e \) - Stała elektrostatyczna (\( 8.99 \times 10^9 \, \frac{Nm^2}{C^2} \)) \( r \) - Odległość od ładunku źródłowego 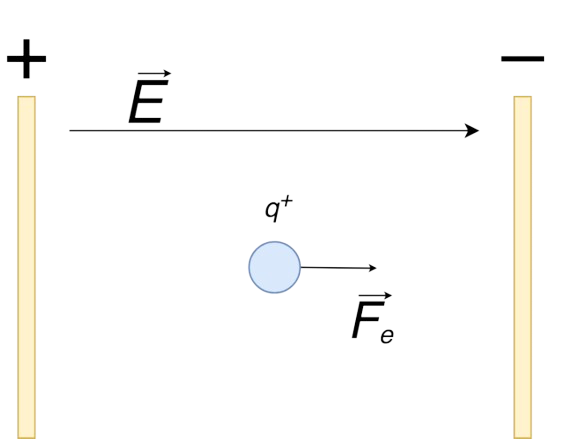
Źródło: Sparkwriter4 Opis:
Natężenie pola elektrycznego wytworzonego przez ładunek punktowy jest zależne od wartości ładunku źródłowego oraz odległości od tego ładunku. |
||
| Potencjał elektryczny | \( V = k_e \frac{Q}{r} = \frac{E_p}{q} \) | |
|
Jednostka Potencjału Elektrycznego (\( V \)): 1 \( V \) (wolt) = 1 \( J / C \) (dżul na kulomb) Legenda Wzoru:\( V \) - Potencjał elektryczny \( Q \) - Ładunek \( k_e \) - Stała elektrostatyczna (\( 8.99 \times 10^9 \, \frac{Nm^2}{C^2} \)) \( r \) - Odległość od ładunku \( E_p \) - Energia potencjalna \( q \) - Ładunek próbny * dla \( q > 0 \) Opis:
Potencjał elektryczny \(V\) pola, dostarcza nam informację o tym, jaką energię potencjalną ma ładunek jednostkowy, w danym punkcie. |
||
| Praca i Energia | ||
| Praca w polu elektrycznym | \( W = q \Delta V \) | |
Legenda Wzoru:\( W \) - Praca \( q \) - Ładunek \( \Delta V \) - Różnica potencjałów (napięcie) 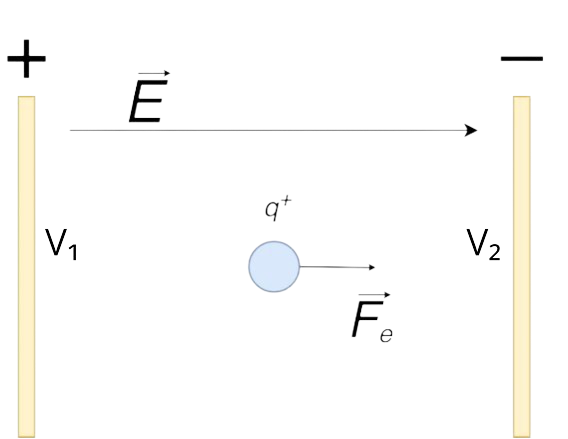
Źródło: | ||
| Praca w polu elektrycznym | \( W = q \Delta V \) | |
Legenda Wzoru:\( W \) - Praca \( q \) - Ładunek \( \Delta V \) - Różnica potencjałów (napięcie) 
Źródło: Sparkwriter4 Opis:
Wzór ten opisuje pracę wykonaną podczas przemieszczania ładunku w polu elektrycznym. Jest to iloczyn ładunku i różnicy potencjałów. |
||
| Energia potencjalna w polu elektrycznym | \( E_p = \frac{k_e q_1 q_2}{r} \) | |
Legenda Wzoru:\( E_p \) - Energia potencjalna \( q_1, q_2 \) - Ładunki \( r \) - Odległość między ładunkami Opis:
Energia potencjalna w polu elektrostatycznym opisuje energię wynikającą z oddziaływania między dwoma ładunkami. Jest ona odwrotnie proporcjonalna do odległości między nimi. |
||
| Kondensatory | ||
| Energia zgromadzona w kondensatorze | \(E_z = \frac{1}{2} C U^2 \) | |
Legenda Wzoru:\( E_z \) - Energia zgromadzona w kondensatorze \( C \) - Pojemność \( U \) - Napięcie Opis:
Wzór ten opisuje energię zgromadzoną w polu elektrycznym kondensatora, która jest zależna od jego pojemności i napięcia między okładkami. |
||
| Pojemność kondensatora | \( C = \frac{Q}{U} = \frac{\epsilon_0 \epsilon_r S}{d} \) | |
Legenda Wzoru:\( C \) - Pojemność \( Q \) - Ładunek zgromadzony na okładkach kondensatora \( U \) - Napięcie między okładkami kondensatora \( \epsilon_0 \) - Przenikalność elektryczna próżni \( \epsilon_r \) - Stała dielektryczna dielektryka \( S \) - Powierzchnia okładek kondensatora \( d \) - Odległość między okładkami kondensatora Opis:
Pojemność kondensatora to stosunek ładunku zgromadzonego na okładkach do napięcia między nimi, wyrażony również wzorem \( C = \frac{\epsilon_0 \epsilon_r S}{d} \). Pojemność zależy od geometrii kondensatora (powierzchni okładek \( S \) i odległości między nimi \( d \)) oraz materiału dielektrycznego między okładkami. Dla kondensatora próżniowego \( \epsilon_r = 1 \), więc wzór upraszcza się do \( C = \frac{\epsilon_0 S}{d} \). |
||
| Związek między napięciem a natężeniem pola (kondensator) | \( E = \frac{U}{d} \) | |
Legenda Wzoru:\( E \) - Natężenie pola elektrycznego \( U \) - Napięcie między okładkami kondensatora \( d \) - Odległość między okładkami kondensatora Opis:
Natężenie pola elektrycznego \( E \) w kondensatorze wynika z napięcia \( U \) między okładkami oraz odległości \( d \) między nimi. Wzór ten pokazuje, że zwiększenie napięcia powoduje wzrost natężenia pola, a zwiększenie odległości zmniejsza natężenie. |
||
| Inne | ||
| Gęstość ładunku | \( \sigma = \frac{Q}{S} \) | |
Legenda Wzoru:\( \sigma \) - Gęstość powierzchniowa ładunku \( Q \) - Całkowity ładunek zgromadzony na przewodniku \( S \) - Powierzchnia, na której ładunek jest zgromadzony Opis:
Gęstość powierzchniowa ładunku na przewodniku kulistym w stanie równowagi jest stała. Zależność ta wynika z faktu, że im mniejszy promień krzywizny przewodnika, tym większa gęstość ładunku zgromadzonego na jego powierzchni. Ostatecznie, gęstość ładunku określa, jak dużo ładunku znajduje się na jednostkowej powierzchni przewodnika. |
||
| Stała elektrostatyczna | \( k_e = \frac{1}{4 \pi \epsilon_0} \) | |
Legenda Wzoru:\( k_e \) - Stała elektrostatyczna \( \epsilon_0 \) - Przenikalność elektryczna próżni Opis:
Wartość stałej elektrostatycznej: \( k_e = 8.99 \times 10^9 \,
\frac{N \cdot m^2}{C^2} \). |
||
| Prawo Gaussa | \( \oint \vec{E} \cdot d\vec{A} = \frac{Q_{wew}}{\epsilon_0} \) | |
Legenda Wzoru:\( \oint \vec{E} \cdot d\vec{A} \) - Strumień elektryczny \( Q_{wew} \) - Ładunek wewnątrz powierzchni \( \epsilon_0 \) - Przenikalność elektryczna próżni Opis:
Prawo Gaussa opisuje związek między strumieniem pola elektrycznego a ładunkiem wewnątrz zamkniętej powierzchni. Jest to jedna z czterech równań Maxwella. |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Najważniejsze wzory | ||
| Prawo Coulomba | \( F = k_e \frac{|q_1 q_2|}{r^2} \) |
Legenda Wzoru:\( F \) - Siła elektrostatyczna \( k_e \) - Stała elektrostatyczna (\( 8.99 \times 10^9 \, \frac{Nm^2}{C^2} \)) \( q_1, q_2 \) - Ładunki \( r \) - Odległość między ładunkami 
Źródło: Dna-Dennis |
| Natężenie pola elektrycznego | \( E = \frac{F}{q} = k_e \frac{|Q|}{r^2} \) |
Legenda Wzoru:\( E \) - Natężenie pola elektrycznego \( F \) - Siła działająca na ładunek próbny \( q \) \( Q \) - Ładunek źródłowy \( r \) - Odległość od ładunku |
| Potencjał elektryczny | \( V = k_e \frac{Q}{r} = \frac{E_p}{q} \) |
Jednostka Potencjału Elektrycznego (\( V \)): 1 \( V \) (wolt) = 1 \( J / C \) (dżul na kulomb) Legenda Wzoru:\( V \) - Potencjał elektryczny \( Q \) - Ładunek \( r \) - Odległość od ładunku \( E_p \) - Energia potencjalna \( q \) - Ładunek próbny * dla \( q > 0 \) Opis:
Potencjał elektryczny \(V\) pola, dostarcza nam informację o tym, jaką energię potencjalną ma ładunek jednostkowy, w danym punkcie. |
| Praca i Energia | ||
| Praca w polu elektrycznym | \( W = q \Delta V \) |
Legenda Wzoru:\( W \) - Praca \( q \) - Ładunek \( \Delta V \) - Różnica potencjałów (napięcie) 
Źródło: Sparkwriter4 Opis:
Wzór ten opisuje pracę wykonaną podczas przemieszczania ładunku w polu elektrycznym. Jest to iloczyn ładunku i różnicy potencjałów. |
| Energia potencjalna w polu elektrycznym | \( E_p = \frac{k_e q_1 q_2}{r} \) |
Legenda Wzoru:\( E_p \) - Energia potencjalna \( q_1, q_2 \) - Ładunki \( r \) - Odległość między ładunkami |
| Kondensatory | ||
| Energia zgromadzona w kondensatorze | \( E_z = \frac{1}{2} C U^2 \) |
Legenda Wzoru:\( E_z \) - Energia zgromadzona w kondensatorze \( C \) - Pojemność \( U \) - Napięcie |
| Pojemność kondensatora | \( C = \frac{Q}{U} = \frac{\epsilon_0 \epsilon_r S}{d} \) |
Legenda Wzoru:\( C \) - Pojemność \( Q \) - Ładunek na okładkach \( U \) - Napięcie \( \epsilon_0 \) - Przenikalność elektryczna próżni \( \epsilon_r \) - Stała dielektryczna |
| Inne | ||
| Gęstość ładunku | \( \sigma = \frac{Q}{S} \) |
Legenda Wzoru:\( \sigma \) - Gęstość powierzchniowa ładunku \( Q \) - Całkowity ładunek zgromadzony na przewodniku \( S \) - Powierzchnia, na której ładunek jest zgromadzony |
| Stała elektrostatyczna | \( k_e = \frac{1}{4 \pi \epsilon_0} \) |
Legenda Wzoru:\( k_e \) - Stała elektrostatyczna \( \epsilon_0 \) - Przenikalność elektryczna próżni |
| Prawo Gaussa | \( \oint \vec{E} \cdot d\vec{A} = \frac{Q_{wew}}{\epsilon_0} \) |
Legenda Wzoru:\( \oint \vec{E} \cdot d\vec{A} \) - Strumień elektryczny \( Q_{wew} \) - Ładunek wewnątrz powierzchni \( \epsilon_0 \) - Przenikalność elektryczna próżni |
Quiz - Elektrostatyka
Elektrostatyka
Elektrostatyka jest działem fizyki zajmującym się badaniem ładunków elektrycznych w stanie spoczynku. Obejmuje badania nad siłami oddziaływania między ładunkami, polem elektrycznym oraz potencjałem elektrycznym.
Elektrostatyka opiera się na prawach opisujących wzajemne oddziaływanie ładunków. Jednym z podstawowych jest prawo Coulomba, które stwierdza, że siła elektrostatyczna między dwoma ładunkami jest wprost proporcjonalna do iloczynu ich wartości, a odwrotnie proporcjonalna do kwadratu odległości między nimi.
W elektrostatyce istotne jest również pojęcie pola elektrycznego, które opisuje siłę działającą na ładunki umieszczone w przestrzeni. Linia sił pola elektrycznego wskazuje kierunek, w którym działa siła na dodatni ładunek testowy, a natężenie pola wyraża jego intensywność.
Elektrostatyka znajduje szerokie zastosowanie w technologii, inżynierii oraz naukach przyrodniczych. Zjawiska elektrostatyczne odgrywają kluczową rolę w działaniu urządzeń takich jak drukarki laserowe, kserokopiarki, monitory kineskopowe, a także w zabezpieczeniach przed wyładowaniami elektrostatycznymi w elektronice.
Badania nad elektrostatyką są istotne również w wielu dziedzinach nauk stosowanych, takich jak projektowanie izolatorów, analiza atmosferycznych wyładowań elektrycznych oraz przemysł farmaceutyczny, gdzie kontrola ładunków elektrostatycznych ma znaczenie w produkcji leków.
Elektrostatyka jest kluczowa dla zrozumienia interakcji między naładowanymi obiektami i wpływu pola elektrycznego na materiały przewodzące i izolatory. Dzięki niej możliwe jest projektowanie nowoczesnych systemów ochronnych i rozwijanie technologii, które minimalizują ryzyko wyładowań elektrostatycznych.
Podsumowując, elektrostatyka jest dziedziną fizyki zajmującą się ładunkami elektrycznymi w spoczynku oraz ich wzajemnymi oddziaływaniami, mającą szerokie zastosowanie praktyczne w technice i nauce.
