Wzory hydrostatyka
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Ciśnienie Hydrostatyczne | \( p = \frac{P}{S}\ = \rho \cdot g \cdot h \) | |
|
Jednostka Ciśnienia Hydrostatyczneg (\(p\)): 1 \(Pa\) (paskal) = 1 \(\frac{N}{m^2}\) Wyprowadzenie wzoru: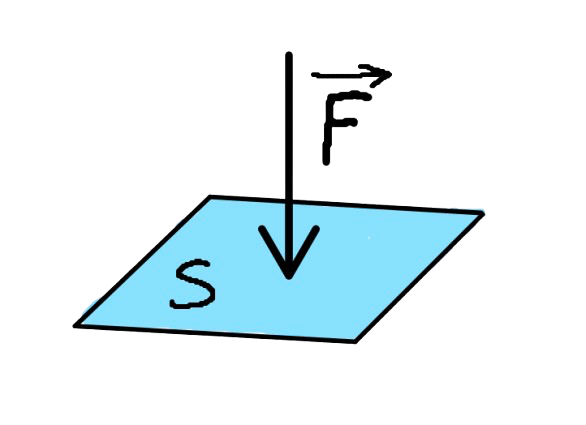
Wyprowadzenie wzoru na ciśnienie hydrostatyczne: Ciśnienie hydrostatyczne \(p\) w cieczy jest definiowane jako stosunek siły nacisku \(F\) do powierzchni \(S\). Wzór na ciśnienie można zapisać jako: \[ p = \frac{F}{S} \] Siła nacisku \(F\) jest równoważna sile ciężkości cieczy znajdującej się nad danym punktem, czyli \(F = m \cdot g\). Masa \(m\) cieczy to iloczyn jej gęstości \(\rho\), objętości \(V\), więc \(F = \rho \cdot V \cdot g\. Ponieważ objętość słupa cieczy \(V\) można zapisać jako \(V = S \cdot h\), podstawiając to do wzoru na siłę otrzymujemy: \[ F = \rho \cdot S \cdot h \cdot g \] Wstawiając to do wzoru na ciśnienie: \( p = \frac{F}{S} \) dostajemy: \[ p = \rho \cdot g \cdot h \] Legenda Wzoru:\( p \) - Ciśnienie \( P \) - Parcie hydrostatyczne (na rysunku \(F\)) \( \rho \) - Gęstość cieczy \( g \) - Przyspieszenie ziemskie \( h \) - Wysokość słupa cieczy \( S \) - Pole powierzchni |
||
| Siła Parcia Hydrostatycznego | \( P = p \cdot S = \rho g h S = \rho g V \)* | |
|
*Jeżeli ściany boczne naczynia nie są prostopadłe do jego dna, to wartość siły parcia cieczy na dno nie jest równa wartości ciężaru cieczy. Jednostka Siły Parcia (\(F\)): 1 \(N\) (niuton) Wyprowadzenie wzoru na siłę parcia hydrostatycznego: Siła parcia hydrostatycznego \(P\) to iloczyn ciśnienia hydrostatycznego \(p\) oraz powierzchni, na którą to ciśnienie działa: \[ P = p \cdot S \] Podstawiając wzór na ciśnienie hydrostatyczne \(p = \rho \cdot g \cdot h\) do równania, otrzymujemy: \[ P = \rho \cdot g \cdot h \cdot S \] Podstawiając do wzoru: \( h \cdot S = V \) otrzymujemy: \[ P = \rho \cdot g \cdot V \] Legenda Wzoru:\( P \) - Parcie hydrostatyczne (na rysunku \(F\)) \( \rho \) - Gęstość cieczy \( g \) - Przyspieszenie ziemskie \( h \) - Wysokość słupa cieczy \( p \) - Ciśnienie \( S \) - Pole powierzchni |
Prawa Hydrostatyki | |
| Prawo Pascala* | \(\frac{F_1}{S_1} = \frac{F_2}{S_2}\) | |

Legenda Wzoru:\(\frac{{F_1}}{{S_1}}\) - Ciśnienie w pierwszym punkcie \(\frac{{F_2}}{{S_2}}\) - Ciśnienie w drugim punkcie \(F_1\) - Siła w pierwszym punkcie \(S_1\) - Powierzchnia w pierwszym punkcie \(F_2\) - Siła w drugim punkcie \(S_2\) - Powierzchnia w drugim punkcie *Wzór opisuje zachowanie ciśnienia w płynach, przy pominięciu wpływu przyciągania ziemskiego. Prawo Pascala:
Prawo Pascala mówi, że wzrost ciśnienia spowodowany wywieraniem nacisku na ciecz o dowolnym kierunku jest w każdym miejscu cieczy jednakowy. |
||
| Prawo Archimedesa, Siła Wyporu | \(F_A = \rho_c \cdot g \cdot V_z\) | |
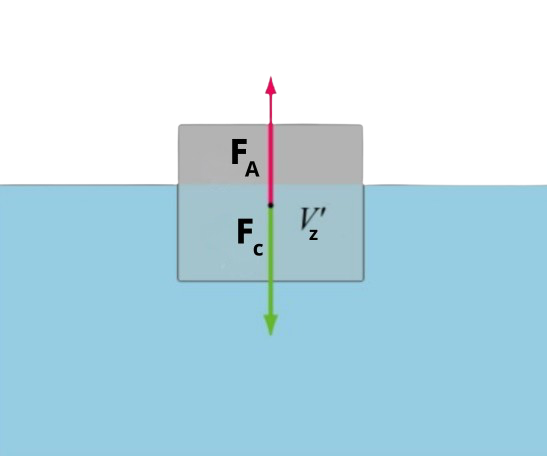
Legenda Wzoru:\(F_A\) - Siła wyporu \(\rho_c\) - Gęstość cieczy \(g\) - Przyspieszenie ziemskie \(V_z\) - Objętość ciała zanurzona w cieczy Prawo Archimedesa:
Prawo Archimedesa mówi, że siła wyporu działająca na ciało zanurzone w cieczy lub gazie jest równa ciężarowi cieczy lub gazu wypartego przez to ciało. |
||
| Prawo Naczyń Połączonych | \(h_1 \cdot \rho_1 = h_2 \cdot \rho_2\) | |

Źródło: Polakko Legenda Wzoru:\(h_1\) - Wysokość cieczy w pierwszym naczyniu \(h_2\) - Wysokość cieczy w drugim naczyniu \(\rho_1\) - Gęstość cieczy w pierwszym naczyniu \(\rho_2\) - Gęstość cieczy w drugim naczyniu Prawo Naczyń Połączonych:
Prawo naczyń połączonych mówi, że poziom cieczy w różnych naczyniach połączonych przewodami otwartymi na ciśnienie atmosferyczne wyrównuje się, jeśli ciecz ma jednolitą gęstość. Jeżeli ciecz jest różnego rodzaju, stosunek wysokości cieczy w każdym naczyniu jest odwrotnie proporcjonalny do gęstości cieczy. |
Inne | |
| Przyśpieszenie ciała zanurzonego w cieczy | \[ a = \frac{{F_c - F_A}}{{m}} = \frac{{m \cdot g - \rho_c \cdot g \cdot V_z}}{{m}} \] | |
Legenda Wzoru:\(F_A\) - Siła wyporu \(F_c\) - Siła ciężkości ciała \(\rho_c\) - Gęstość cieczy \(g\) - Przyspieszenie ziemskie \(V_z\) - Objętość ciała zanurzona w cieczy Wyprowadzenie wzoru:Druga zasada dynamiki dla ciała mówi, że siła wypadkowa \( F \) działająca na ciało jest równa iloczynowi masy \( m \) i przyspieszenia \( a \), czyli \( F = m \cdot a \). Na ciało zanurzone w cieczy, działają dwie siły: siła ciężkości \( F_c\) i siła wyporu \( F_A \). Tworząc rówanie sił dla tego ciała dostajemy, że siła wypadkowa: \[ F = F_c - F_A \] Zgodnie z prawem Archimedesa, siła wyporu jest równa ciężarowi wypartej cieczy, czyli: \( F_A = \rho_c \cdot g \cdot V_z \) Za siłę ciężkości (\( F_c \)) podstawimy \( m \cdot g \) Otrzymujemy: \( F = m \cdot a = F_c - F_A = m \cdot g - \rho_c \cdot g \cdot V_z \) |
||
| Objętość Zanurzona w Cieczy | \(V_z = V_0 \cdot \frac{\rho_{\text{ciała}}}{\rho_{\text{cieczy}}}\) gdy \(\rho_{\text{ciała}} \leq \rho_{\text{cieczy}}\) | |
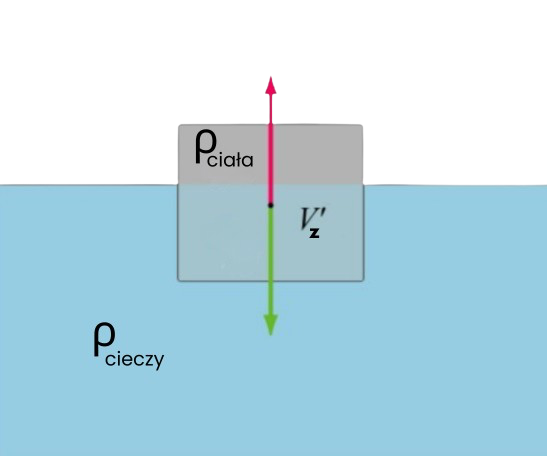
Legenda Wzoru:\(V_z\) - Objętość ciała zanurzona w cieczy \(V_0\) - Całkowita objętość ciała \(\rho_{\text{ciała}}\) - Gęstość ciała \(\rho_{\text{cieczy}}\) - Gęstość cieczy Opis Wzoru:
Wzór określa objętość ciała zanurzoną w cieczy, gdy gęstość ciała jest mniejsza lub równa gęstości cieczy. |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Ciśnienie Hydrostatyczne | \( p = \frac{P}{S} = \rho \cdot g \cdot h \) |
Jednostka Ciśnienia Hydrostatycznego (\(p\)): 1 \(Pa\) (paskal) = 1 \(\frac{N}{m^2}\) Wyprowadzenie wzoru:
Wyprowadzenie wzoru na ciśnienie hydrostatyczne: Ciśnienie hydrostatyczne \(p\) w cieczy jest definiowane jako stosunek siły nacisku \(F\) do powierzchni \(S\). Wzór na ciśnienie można zapisać jako: \[ p = \frac{F}{S} \] Siła nacisku \(F\) jest równoważna sile ciężkości cieczy znajdującej się nad danym punktem, czyli \(F = m \cdot g\). Masa \(m\) cieczy to iloczyn jej gęstości \(\rho\), objętości \(V\), więc \(F = \rho \cdot V \cdot g\. Ponieważ objętość słupa cieczy \(V\) można zapisać jako \(V = S \cdot h\), podstawiając to do wzoru na siłę otrzymujemy: \[ F = \rho \cdot S \cdot h \cdot g \] Wstawiając to do wzoru na ciśnienie: \(p = \frac{F}{S}\), dostajemy: \[ p = \rho \cdot g \cdot h \] Legenda Wzoru:\( p \) - Ciśnienie \( P \) - Parcie hydrostatyczne (na rysunku \(F\)) \( \rho \) - Gęstość cieczy \( g \) - Przyspieszenie ziemskie \( h \) - Wysokość słupa cieczy \( S \) - Pole powierzchni |
| Siła Parcia Hydrostatycznego | \( P = p \cdot S = \rho g h S = \rho g V \)* |
*Jeżeli ściany boczne naczynia nie są prostopadłe do jego dna, to wartość siły parcia cieczy na dno nie jest równa wartości ciężaru cieczy. Jednostka Siły Parcia (\(F\)): 1 \(N\) (niuton) Wyprowadzenie wzoru na siłę parcia hydrostatycznego: Siła parcia hydrostatycznego \(P\) to iloczyn ciśnienia hydrostatycznego \(p\) oraz powierzchni, na którą to ciśnienie działa: \[ P = p \cdot S \] Podstawiając wzór na ciśnienie hydrostatyczne \(p = \rho \cdot g \cdot h\) do równania, otrzymujemy: \[ P = \rho \cdot g \cdot h \cdot S \] Podstawiając do wzoru: \( h \cdot S = V \), otrzymujemy: \[ P = \rho \cdot g \cdot V \] Legenda Wzoru:\( P \) - Parcie hydrostatyczne (na rysunku \(F\)) \( \rho \) - Gęstość cieczy \( g \) - Przyspieszenie ziemskie \( h \) - Wysokość słupa cieczy \( p \) - Ciśnienie \( S \) - Pole powierzchni |
| Prawa Hydrostatyczne | ||
| Prawo Pascala* | \(\frac{F_1}{S_1} = \frac{F_2}{S_2}\) |

Legenda Wzoru:\(\frac{{F_1}}{{S_1}}\) - Ciśnienie w pierwszym punkcie \(\frac{{F_2}}{{S_2}}\) - Ciśnienie w drugim punkcie \(F_1\) - Siła w pierwszym punkcie \(S_1\) - Powierzchnia w pierwszym punkcie \(F_2\) - Siła w drugim punkcie \(S_2\) - Powierzchnia w drugim punkcie *Wzór opisuje zachowanie ciśnienia w płynach, przy pominięciu wpływu przyciągania ziemskiego. Prawo Pascala mówi, że wzrost ciśnienia spowodowany wywieraniem nacisku na ciecz o dowolnym kierunku jest w każdym miejscu cieczy jednakowy. |
| Prawo Archimedesa, Siła Wyporu | \(F_A = \rho_c \cdot g \cdot V_z\) |

Legenda Wzoru:\(F_A\) - Siła wyporu \(\rho_c\) - Gęstość cieczy \(g\) - Przyspieszenie ziemskie \(V_z\) - Objętość ciała zanurzona w cieczy Prawo Archimedesa mówi, że siła wyporu działająca na ciało zanurzone w cieczy lub gazie jest równa ciężarowi cieczy lub gazu wypartego przez to ciało. |
| Prawo Naczyń Połączonych | \(h_1 \cdot \rho_1 = h_2 \cdot \rho_2\) |

Źródło: Polakko Legenda Wzoru:\(h_1\) - Wysokość cieczy w pierwszym naczyniu \(h_2\) - Wysokość cieczy w drugim naczyniu \(\rho_1\) - Gęstość cieczy w pierwszym naczyniu \(\rho_2\) - Gęstość cieczy w drugim naczyniu Prawo naczyń połączonych mówi, że poziom cieczy w różnych naczyniach połączonych przewodami otwartymi na ciśnienie atmosferyczne wyrównuje się, jeśli ciecz ma jednolitą gęstość. Jeżeli ciecz jest różnego rodzaju, stosunek wysokości cieczy w każdym naczyniu jest odwrotnie proporcjonalny do gęstości cieczy. |
| Inne | ||
| Przyśpieszenie ciała zanurzonego w cieczy | \( a = \frac{{F_c - F_A}}{{m}} = \frac{{m \cdot g - \rho_c \cdot g \cdot V_z}}{{m}} \) |
Legenda Wzoru:\(F_A\) - Siła wyporu \(F_c\) - Siła ciężkości ciała \(\rho_c\) - Gęstość cieczy \(g\) - Przyspieszenie ziemskie \(V_z\) - Objętość ciała zanurzona w cieczy Wyprowadzenie wzoru:Druga zasada dynamiki dla ciała mówi, że siła wypadkowa \( F \) działająca na ciało jest równa iloczynowi masy \( m \) i przyspieszenia \( a \), czyli \( F = m \cdot a \). Na ciało zanurzone w cieczy, działają dwie siły: siła ciężkości \( F_c\) i siła wyporu \( F_A \). Tworząc rówanie sił dla tego ciała dostajemy, że siła wypadkowa: \[ F = F_c - F_A \] Zgodnie z prawem Archimedesa, siła wyporu jest równa ciężarowi wypartej cieczy, czyli: \( F_A = \rho_c \cdot g \cdot V_z \) Za siłę ciężkości (\( F_c \)) podstawimy \( m \cdot g \) Otrzymujemy: \( F = m \cdot a = F_c - F_A = m \cdot g - \rho_c \cdot g \cdot V_z \) |
| Objętość Zanurzona w Cieczy | \(V_z = V_0 \cdot \frac{\rho_{\text{ciała}}}{\rho_{\text{cieczy}}}\) dla \(\rho_{\text{ciała}} \leq \rho_{\text{cieczy}}\) |

Legenda Wzoru:\(V_z\) - Objętość ciała zanurzona w cieczy \(V_0\) - Całkowita objętość ciała \(\rho_{\text{ciała}}\) - Gęstość ciała \(\rho_{\text{cieczy}}\) - Gęstość cieczy Wzór określa objętość ciała zanurzoną w cieczy, gdy gęstość ciała jest mniejsza lub równa gęstości cieczy. |
Quiz - Hydrostatyka
Hydrostatyka
Hydrostatyka jest działem fizyki zajmującym się statyką płynów, czyli cieczy oraz gazów, w spoczynku. Badaniem obejmuje m.in. ciśnienie w płynach, zasady równowagi hydrostatycznej oraz zastosowania w praktyce.
Podstawowymi pojęciami w hydrostatyce są ciśnienie hydrostatyczne, które jest równomierne w płynie i działa prostopadle do każdej powierzchni, oraz zasada równowagi hydrostatycznej, która mówi o równowadze sił na każdym punkcie płynu.
Hydrostatyka ma liczne zastosowania praktyczne, m.in. w konstrukcji zbiorników ciśnieniowych, układów hydraulicznych czy analizie działania pomp i sprężarek.
Badania w hydrostatyce pozwalają na zrozumienie zjawisk związanych z zachowaniem się płynów w warunkach spoczynku, co ma zastosowanie w wielu dziedzinach inżynierii oraz w życiu codziennym.
Hydrostatyka jest również ściśle związana z innymi dziedzinami fizyki, takimi jak dynamika płynów, termodynamika oraz mechanika płynów..
Zainteresowanie hydrostatyką jest istotne zarówno dla naukowców, inżynierów, jak i osób zainteresowanych fizyką oraz technikami wykorzystującymi płyny w różnych procesach i konstrukcjach.
Podsumowując, hydrostatyka jest dziedziną fizyki zajmującą się statyką płynów, która ma liczne zastosowania praktyczne oraz jest istotna dla zrozumienia zachowań cieczy w różnych warunkach.
