Wzory prąd stały
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Prawa | ||
| Prawo Ohma | \( I = \frac{I=U}{R} \) | |
Legenda Wzoru:\( V \) - Napięcie (wolt) \( I \) - Natężenie prądu (amper) \( R \) - Opór (om) Opis:
Prawo Ohma wiąże napięcie przyłożone do przewodnika z natężeniem przepływającego prądu i oporem przewodnika. |
||
| Pierwsze prawo Kirchhoffa | \( \sum I_{we} = \sum I_{wy} \) | |
Legenda Wzoru:\( \sum I_{we} \) - Suma prądów wpływających do węzła \( \sum I_{wy} \) - Suma prądów wypływających z węzła 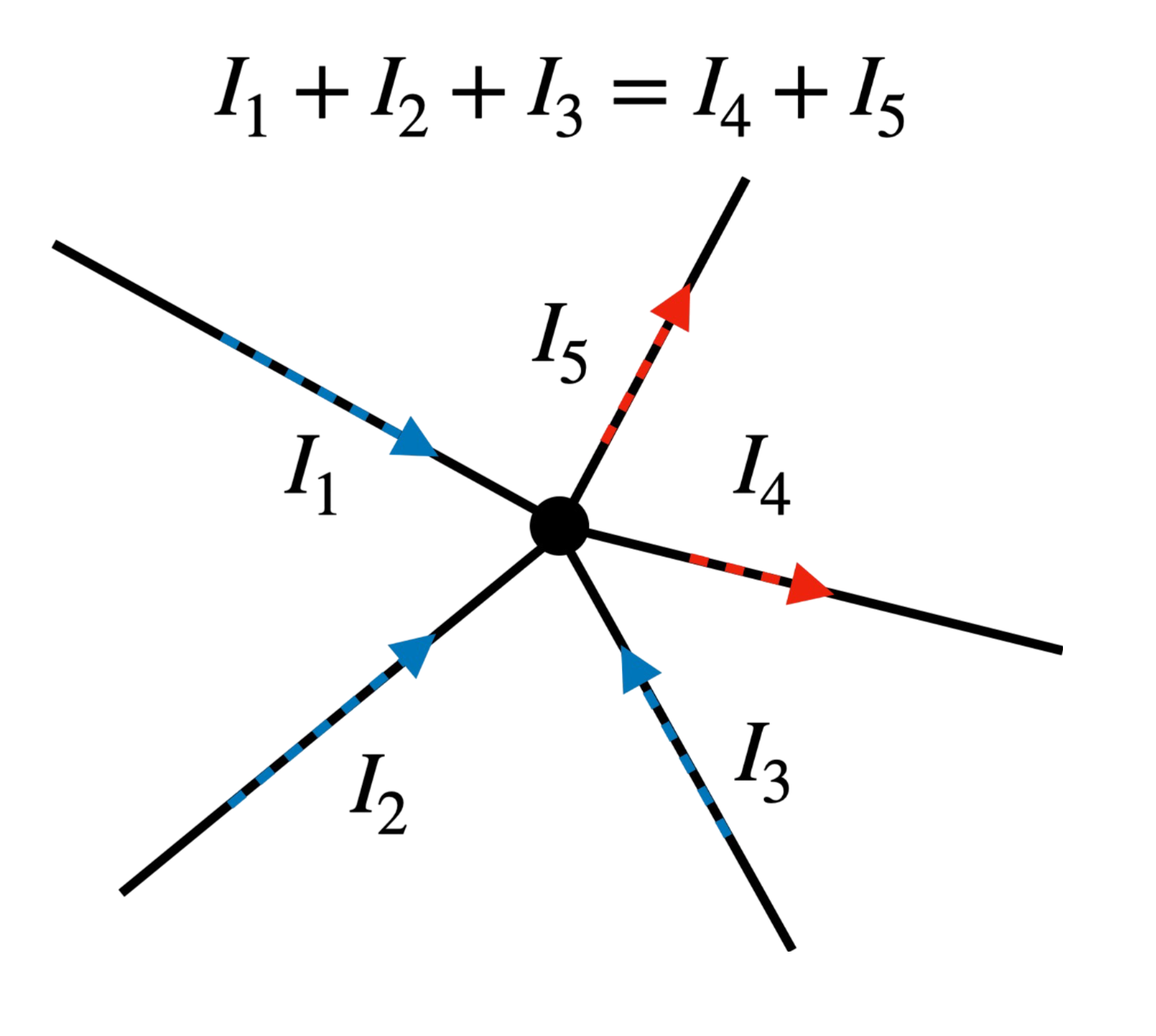
Opis:
Pierwsze prawo Kirchhoffa mówi, że suma prądów wpływających do węzła jest równa sumie prądów wypływających z węzła. Wynika to z zasady zachowania ładunku elektrycznego. |
||
| Drugie prawo Kirchhoffa | \( \sum_{k=1}^{n} \mathcal{E}_k + \sum_{k=1}^{m} I_k R_k = 0 \) | |
|
Opis:
Drugie prawo Kirchhoffa mówi, że suma napięć w obwodzie zamkniętym jest równa zero. Uwzględnia ono zarówno spadki napięcia, jak i napięcia źródeł. |
||
| Praca, Moc i Energia | ||
| Praca prądu elektrycznego | \( W = U I t \) | |
Legenda Wzoru:\( W \) - Praca (dżule) \( U \) - Napięcie \( I \) - Natężenie prądu \( t \) - Czas przepływu prądu Opis:
Praca prądu elektrycznego jest iloczynem napięcia, natężenia i czasu przepływu prądu. |
||
| Moc prądu elektrycznego | \( P = U I = I^2 R = \frac{U^2}{R} \) | |
Legenda Wzoru:\( P \) - Moc (waty) \( U \) - Napięcie \( I \) - Natężenie prądu \( R \) - Opór Opis:
Moc prądu elektrycznego wyrażana jest jako iloczyn napięcia i natężenia lub kwadrat natężenia pomnożony przez opór. |
||
| Energia wewnętrzna przewodnika (Ciepło Joule’a) | \( Q = I^2 R t \) | |
Legenda Wzoru:\( Q \) - Ciepło wytworzone w przewodniku (dżule) \( I \) - Natężenie prądu (ampery) \( R \) - Opór przewodnika (omy) \( t \) - Czas przepływu prądu (sekundy) 
Opis:
Wzór Joule’a-Lenza opisuje ilość energii zamienianej na ciepło w przewodniku w wyniku przepływu prądu. Ciepło \( Q \) jest proporcjonalne do kwadratu natężenia, oporu przewodnika oraz czasu przepływu prądu. |
||
| Oporniki | ||
| Łączenie oporników (szeregowe) | \( R_z = R_1 + R_2 + R_3 + \dots \) | |
Legenda Wzoru:\( R_z \) - Całkowity opór w połączeniu szeregowym (Opór zastępczy) \( R_1, R_2, R_3 \) - Opory poszczególnych rezystorów 
Opis:
W połączeniu szeregowym oporników całkowity opór jest sumą oporów poszczególnych elementów. |
||
| Łączenie oporników (równoległe) | \( \frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots \) | |
Legenda Wzoru:\( R_z \) - Całkowity opór w połączeniu równoległym (Opór zastępczy) \( R_1, R_2, R_3 \) - Opory poszczególnych rezystorów 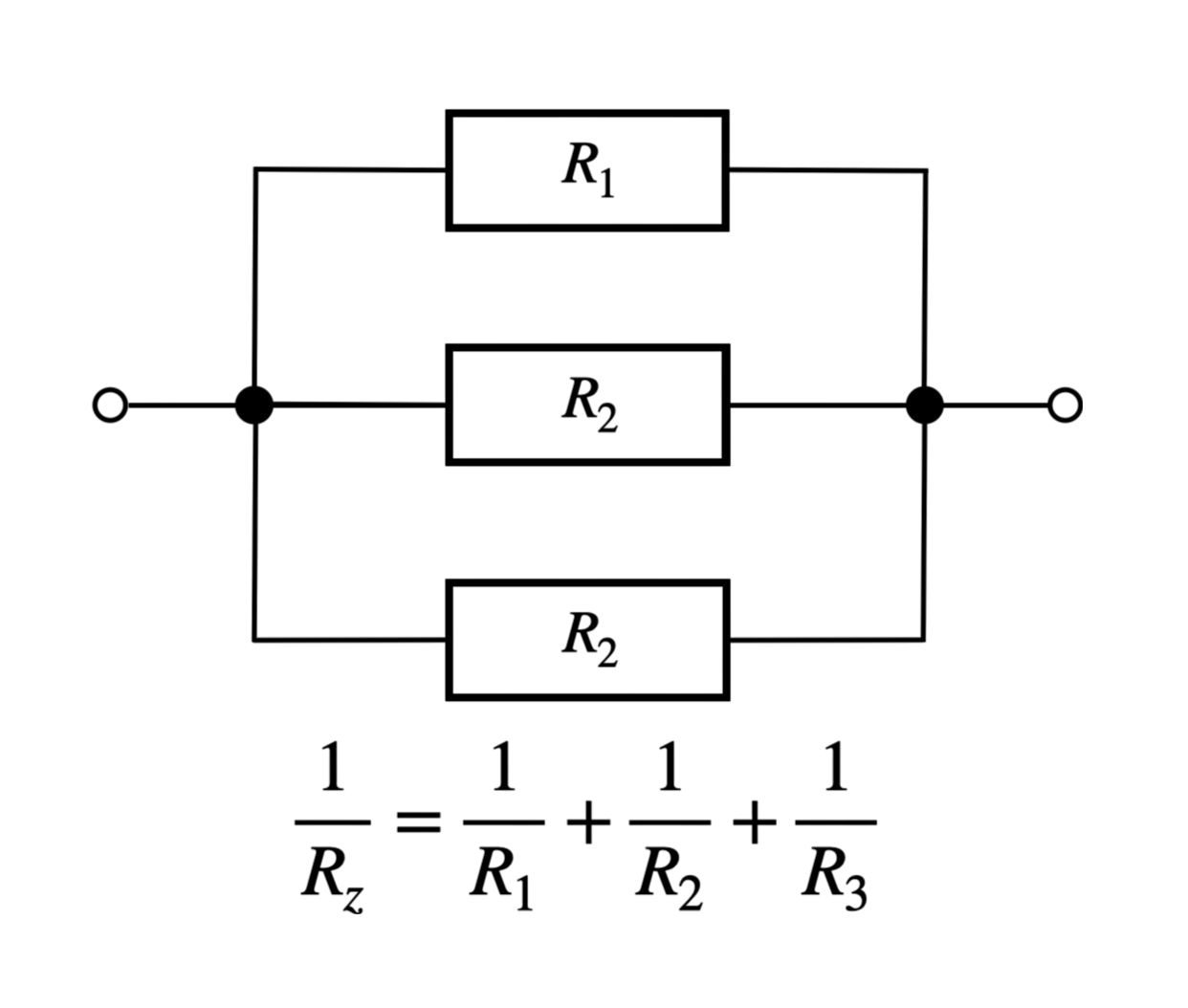
Opis:
W połączeniu równoległym odwrotność całkowitego oporu jest sumą odwrotności oporów poszczególnych elementów. |
||
| Opór a opór właściwy | \( R = \rho \frac{L}{S} \) | |
Legenda Wzoru:\( R \) - Opór przewodnika \( \rho \) - Opór właściwy materiału \( L \) - Długość przewodnika \( S \) - Pole przekroju poprzecznego przewodnika Opis:
Opór przewodnika zależy od oporu właściwego materiału, jego długości oraz pola przekroju poprzecznego. Materiały o niższym oporze właściwym, takie jak miedź czy aluminium, mają mniejszy opór. |
||
| Opór przewodnika a temperatura | \( R = R_0(1 + \alpha T) \) | |
Legenda Wzoru:\( R \) - Opór w temperaturze \( T \) \( R_0 \) - Opór w temperaturze odniesienia (np. \( 0^\circ C \)) \( \alpha \) - Współczynnik temperaturowy oporu \( T \) - Zmiana temperatury Opis:
Wzór ten opisuje zmianę oporu przewodnika w zależności od temperatury, zakładając liniową zależność w szerokim zakresie temperatur. |
||
| Inne Wzory | ||
| Natężenie prądu - mikroskopowy punkt widzenia | \( I = n q v_d S \) | |
Legenda Wzoru:\( I \) - Natężenie prądu \( n \) - Liczba nośników ładunku na jednostkę objętości \( q \) - Ładunek pojedynczego nośnika \( v_d \) - Prędkość dryfu \( S \) - Pole przekroju przewodnika Opis:
Wzór ten opisuje natężenie prądu elektrycznego jako zależne od liczby nośników ładunku, ich prędkości dryfu, ładunku i pola przekroju przewodnika. |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Prawa | ||
| Prawo Ohma | \( I = \frac{U}{R} \) |
Legenda Wzoru:\( V \) - Napięcie (wolt) \( I \) - Natężenie prądu (amper) \( R \) - Opór (om) Opis:
Prawo Ohma wiąże napięcie przyłożone do przewodnika z natężeniem przepływającego prądu i oporem przewodnika. |
| Pierwsze prawo Kirchhoffa | \( \sum I_{we} = \sum I_{wy} \) |
Legenda Wzoru:\( \sum I_{we} \) - Suma prądów wpływających do węzła \( \sum I_{wy} \) - Suma prądów wypływających z węzła 
Opis:
Pierwsze prawo Kirchhoffa mówi, że suma prądów wpływających do węzła jest równa sumie prądów wypływających z węzła. Wynika to z zasady zachowania ładunku elektrycznego. |
| Drugie prawo Kirchhoffa | \( \sum_{k=1}^{n} \mathcal{E}_k + \sum_{k=1}^{m} I_k R_k = 0 \) |
Opis:
Drugie prawo Kirchhoffa mówi, że suma napięć w obwodzie zamkniętym jest równa zero. Uwzględnia ono zarówno spadki napięcia, jak i napięcia źródeł. |
| Praca, Moc i Energia | ||
| Praca prądu elektrycznego | \( W = U I t \) |
Legenda Wzoru:\( W \) - Praca (dżule) \( U \) - Napięcie \( I \) - Natężenie prądu \( t \) - Czas przepływu prądu Opis:
Praca prądu elektrycznego jest iloczynem napięcia, natężenia i czasu przepływu prądu. |
| Moc prądu elektrycznego | \( P = U I = I^2 R = \frac{U^2}{R} \) |
Legenda Wzoru:\( P \) - Moc (waty) \( U \) - Napięcie \( I \) - Natężenie prądu \( R \) - Opór Opis:
Moc prądu elektrycznego wyrażana jest jako iloczyn napięcia i natężenia lub kwadrat natężenia pomnożony przez opór. |
| Energia wewnętrzna przewodnika (Ciepło Joule’a) | \( Q = I^2 R t \) |
Legenda Wzoru:\( Q \) - Ciepło wytworzone w przewodniku (dżule) \( I \) - Natężenie prądu (ampery) \( R \) - Opór przewodnika (omy) \( t \) - Czas przepływu prądu (sekundy) 
Opis:
Wzór Joule’a-Lenza opisuje ilość energii zamienianej na ciepło w przewodniku w wyniku przepływu prądu. Ciepło \( Q \) jest proporcjonalne do kwadratu natężenia, oporu przewodnika oraz czasu przepływu prądu. |
| Oporniki | ||
| Łączenie oporników (szeregowe) | \( R_z = R_1 + R_2 + R_3 + \dots \) |
Legenda Wzoru:\( R_z \) - Całkowity opór w połączeniu szeregowym \( R_1, R_2, R_3 \) - Opory poszczególnych rezystorów 
Opis:
W połączeniu szeregowym oporników całkowity opór jest sumą oporów poszczególnych elementów. |
| Łączenie oporników (równoległe) | \( \frac{1}{R_p} = \frac{1}{R_1} + \frac{1}{R_2} + \frac{1}{R_3} + \dots \) |
Legenda Wzoru:\( R_z \) - Całkowity opór w połączeniu równoległym \( R_1, R_2, R_3 \) - Opory poszczególnych rezystorów 
Opis:
W połączeniu równoległym odwrotność całkowitego oporu jest sumą odwrotności oporów poszczególnych elementów. |
| Opór a opór właściwy | \( R = \rho \frac{L}{S} \) |
Legenda Wzoru:\( R \) - Opór przewodnika \( \rho \) - Opór właściwy materiału \( L \) - Długość przewodnika \( S \) - Pole przekroju poprzecznego przewodnika Opis:
Opór przewodnika zależy od oporu właściwego materiału, jego długości oraz pola przekroju poprzecznego. |
| Opór przewodnika a temperatura | \( R = R_0(1 + \alpha T) \) |
Legenda Wzoru:\( R \) - Opór w temperaturze \( T \) \( R_0 \) - Opór w temperaturze odniesienia \( \alpha \) - Współczynnik temperaturowy oporu \( T \) - Zmiana temperatury Opis:
Wzór ten opisuje zmianę oporu przewodnika w zależności od temperatury, zakładając liniową zależność w szerokim zakresie temperatur. |
| Inne Wzory | ||
| Natężenie prądu - mikroskopowy punkt widzenia | \( I = n q v_d S \) |
Legenda Wzoru:\( I \) - Natężenie prądu \( n \) - Liczba nośników ładunku na jednostkę objętości \( q \) - Ładunek pojedynczego nośnika \( v_d \) - Prędkość dryfu \( S \) - Pole przekroju przewodnika Opis:
Wzór ten opisuje natężenie prądu elektrycznego jako zależne od liczby nośników ładunku, ich prędkości dryfu, ładunku i pola przekroju przewodnika. |
Quiz - Prąd Stały
Prąd Stały
Prąd stały (DC, ang. Direct Current) to przepływ ładunków elektrycznych w jednym, niezmiennym kierunku. Charakteryzuje się stałą wartością natężenia oraz napięcia w czasie.
Prąd stały występuje, gdy ładunki elektryczne przepływają przez przewodnik, taki jak metalowy drut, w sposób ciągły i jednostajny. Jest podstawą działania wielu urządzeń elektronicznych i systemów energetycznych.
Podstawowym źródłem prądu stałego są ogniwa elektrochemiczne, takie jak baterie i akumulatory, które dostarczają energię elektryczną w sposób niezależny od sieci energetycznej. W przemyśle, prostowniki przekształcają prąd zmienny w prąd stały, umożliwiając jego zastosowanie w szerokim zakresie technologii.
Prąd stały charakteryzuje się prostotą w zastosowaniu, szczególnie w układach, gdzie wymagane jest stabilne napięcie, takich jak urządzenia przenośne, elektronika użytkowa czy systemy zasilania awaryjnego.
Istotnym pojęciem związanym z prądem stałym jest rezystancja, która określa, jak bardzo przewodnik przeciwstawia się przepływowi prądu. Zgodnie z prawem Ohma, natężenie prądu w obwodzie jest wprost proporcjonalne do napięcia i odwrotnie proporcjonalne do rezystancji.
Prąd stały odgrywa kluczową rolę w technologiach takich jak fotowoltaika, ładowanie pojazdów elektrycznych, systemy magazynowania energii oraz w zasilaczach elektronicznych. Jest również szeroko wykorzystywany w mikroelektronice i układach scalonych.
Współczesne badania nad prądem stałym koncentrują się na zwiększeniu wydajności jego wytwarzania i dystrybucji, szczególnie w odniesieniu do odnawialnych źródeł energii, takich jak panele słoneczne czy turbiny wiatrowe.
Podsumowując, prąd stały jest kluczowym pojęciem w fizyce i technice, umożliwiającym rozwój zaawansowanych systemów energetycznych i urządzeń elektronicznych, dzięki swojej stabilności i szerokim zastosowaniom praktycznym.
