Wzory ruch harmoniczny
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Okres Drgań Układu Masa-Sprężyna | \( T = 2\pi \sqrt{\frac{m}{k}} \) | |
Legenda Wzoru:\( T \) - Okres drgań \( m \) - Masa \( k \) - Stała sprężystości Wyprowadzenie wzoru:1. Zależność początkowa: Zaczynamy od równania \( m \omega^2 = k \), które wiąże masę \( m \), częstotliwość kątową \( \omega \) oraz stałą sprężystości \( k \). 2. Izolacja częstotliwości kątowej: Rozwiązujemy równanie dla \( \omega^2 \), dzieląc obie strony przez \( m \): \[ \omega^2 = \frac{k}{m} \] 3. Wyznaczenie \( \omega \): Bierzemy pierwiastek z obu stron, aby znaleźć częstotliwość kątową: \[ \omega = \sqrt{\frac{k}{m}} \] 4. Okres Drgań: Okres drgań jest odwrotnością częstotliwości kątowej, co prowadzi do wzoru na okres: \[ T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}} \] |
||
| Okres Drgań Wahadła Matematycznego | \( T = 2\pi \sqrt{\frac{l}{g}} \) | |
Legenda Wzoru:\( T \) - Okres drgań \( l \) - Długość wahadła \( g \) - Przyspieszenie ziemskie (około 9.81 m/s²) Wyprowadzenie wzoru: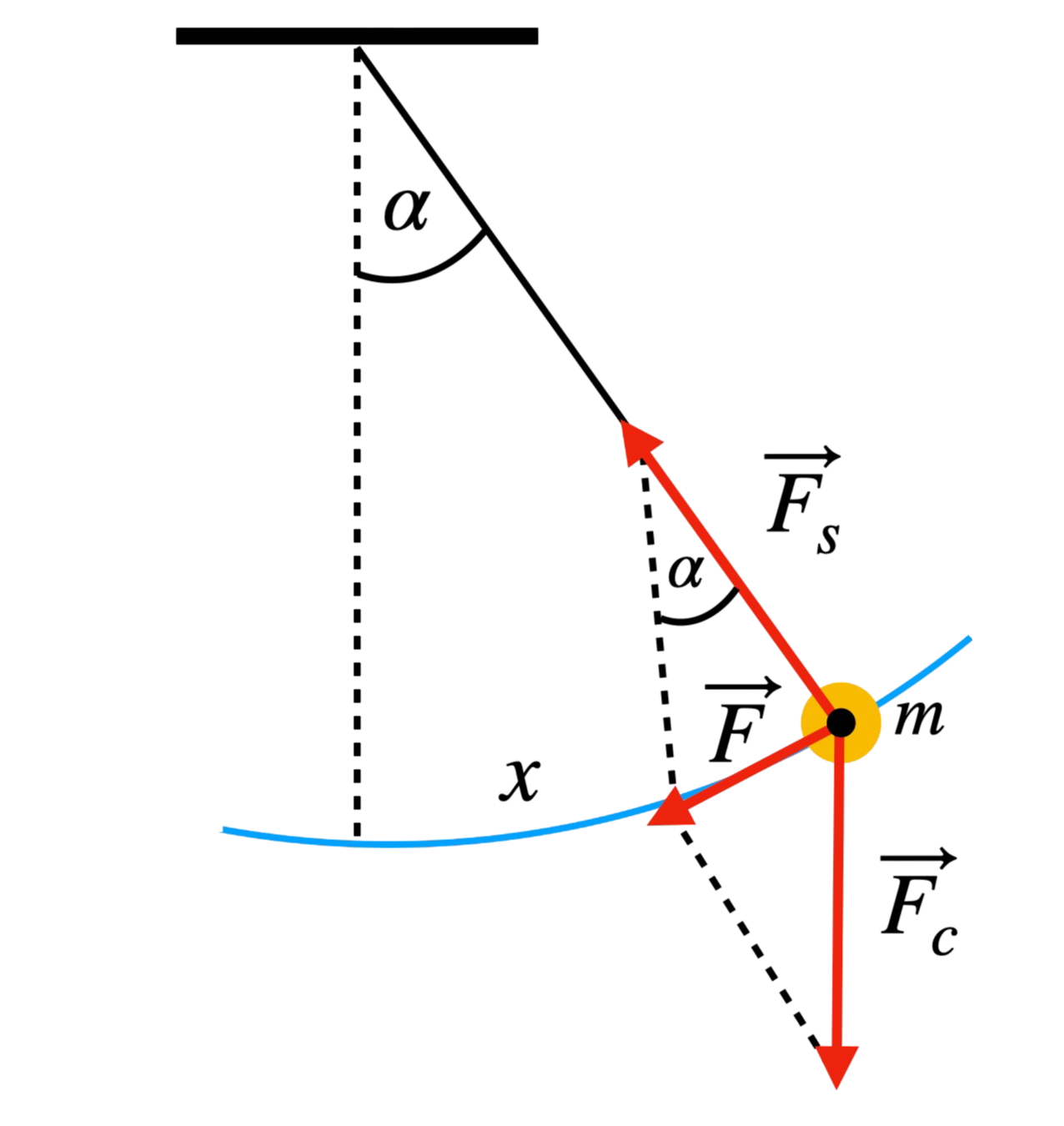
1. Przybliżenie: Zakładamy, że kąt wychylenia \(\alpha\) jest mały, co pozwala przyjąć, że \(\sin \alpha \approx \alpha\). Wychylenie \(\alpha\) można wyrazić jako \(\frac{x}{l}\), gdzie \(x\) to przemieszczenie, a \(l\) to długość wahadła. 2. Siła Przywracająca: Siła działająca na wahadło to \( F = mg \sin \alpha \), która dla małych kątów staje się \( F = mg \frac{x}{l} \). Siła skierowana jest do położenia równowagi, więc: \[ F_x = -mg \frac{x}{l} \] 3. Równanie Ruchu: Siła sprężystości: \( F = -kx \), czyli: \[ -kx = -mg \frac{x}{l} \] z czego można wyznaczyc k: \[ k = \frac{mg}{l} \] 4. Podstawiane do wzoru: Podstawiamy wyżej wzynaczone k do wzoru, otrzymujemy \(\omega^2 = \frac{g}{l}\), więc: \[ \omega = \sqrt{\frac{g}{l}} \] co daje wzór na okres wahadła: \[ T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{l}{g}} \] |
||
| Siła Sprężystości | \( F = k \cdot |x| = m \cdot \omega^2 \cdot x\) | |
Legenda Wzoru:\( F \) - Siła sprężystości \( k \) - Stała sprężystości \( x \) - Wydłużenie (lub ściśnięcie) sprężyny 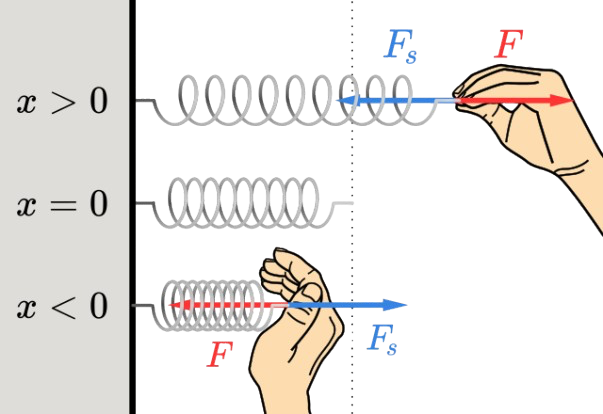
Źródło: MikeRun Opis:Siła sprężystości to siła, którą sprężyna działa na ciało, gdy jest rozciągnięta lub ściśnięta o wartość \( x \). Siła ta jest proporcjonalna do wydłużenia lub skrócenia sprężyny zgodnie z prawem Hooke'a, \( F = k \cdot x \), gdzie \( k \) to stała sprężystości, a \( x \) to odległość od pozycji równowagi. |
||
| Współczynnik Sprężystości | \( k = -m \cdot \omega^2 = \frac{-F}{x} \) | |
Legenda Wzoru:\( k \) - Stała sprężystości \( m \) - Masa układu \( \omega \) - Częstotliwość kątowa \( F \) - Siła działająca na sprężynę \( x \) - Wydłużenie sprężyny 
Źródło: MikeRun |
Energia | |
| Energia Potencjalna w Ruchu Harmonicznym | \( E_p = \frac{1}{2} k x^2 \) | |
|
Źródło:
MikeRun
|
Energia | |
| Energia Potencjalna w Ruchu Harmonicznym | \( E_p = \frac{1}{2} k x^2 \) | |
Legenda Wzoru:\( E_p \) - Energia potencjalna \( k \) - Stała sprężystości \( x \) - Wychylenie z położenia równowagi Opis:Energia potencjalna w ruchu harmonicznym wyrażana jest wzorem \( E_p = \frac{1}{2} k x^2 \), gdzie \( k \) to stała sprężystości, a \( x \) to wychylenie z położenia równowagi. Energia ta osiąga swoje maksimum, gdy wychylenie \( x \) jest największe, a sprężyna jest maksymalnie rozciągnięta lub ściśnięta. |
||
| Energia Kinetyczna w Ruchu Harmonicznym | \( E_k = \frac{1}{2} k (A^2 - x^2) \) | |
Legenda Wzoru:\( E_k \) - Energia kinetyczna \( k \) - Stała sprężystości \( A \) - Amplituda drgań \( x \) - Wychylenie z położenia równowagi Opis:Energia kinetyczna w ruchu harmonicznym wyrażona jest wzorem \( E_k = \frac{1}{2} k (A^2 - x^2) \), gdzie \( A \) to amplituda, a \( x \) to wychylenie. Energia kinetyczna jest największa w położeniu równowagi, kiedy \( x = 0 \), a najmniejsza w skrajnych wychyleniach, kiedy \( x = A \), gdzie energia kinetyczna spada do zera. |
||
| Energia Całkowita w Ruchu Harmonicznym | \( E_c = \frac{1}{2} k A^2 \) | |
Legenda Wzoru:\( E_c \) - Energia całkowita \( k \) - Stała sprężystości \( A \) - Amplituda drgań Opis:Energia całkowita w ruchu harmonicznym wyrażona jest wzorem \( E_c = \frac{1}{2} k A^2 \), gdzie \( A \) to amplituda drgań, czyli maksymalne wychylenie z położenia równowagi. Energia całkowita w ruchu harmonicznym jest sumą energii kinetycznej i potencjalnej, i pozostaje stała w czasie, o ile nie ma strat energii. |
Wzory Ogólne | |
| Położenie w Ruchu Harmonicznym | \(x = A \cdot \sin(\omega t + \phi)\) | |
Legenda Wzoru:\(x\) - Położenie \(A\) - Amplituda \(\omega\) - Częstość kołowa \(t\) - Czas \(\phi\) - Faza początkowa 
|
||
| Prędkość w Ruchu Harmonicznym | \(V_x = \omega A \cdot \cos(\omega t + \phi)\) | |
Legenda Wzoru:\(V_x\) - Prędkość \(A\) - Amplituda \(\omega\) - Częstość kołowa \(t\) - Czas \(\phi\) - Faza początkowa 
|
||
| Przyspieszenie w Ruchu Harmonicznym | \( a_x = -\omega^2 \cdot A \cdot \sin(\omega \cdot t + \phi) \) | |
Legenda Wzoru:\( a_x \) - Przyspieszenie \( A \) - Amplituda \( \omega \) - Częstość kołowa \( t \) - Czas \( \phi \) - Faza początkowa 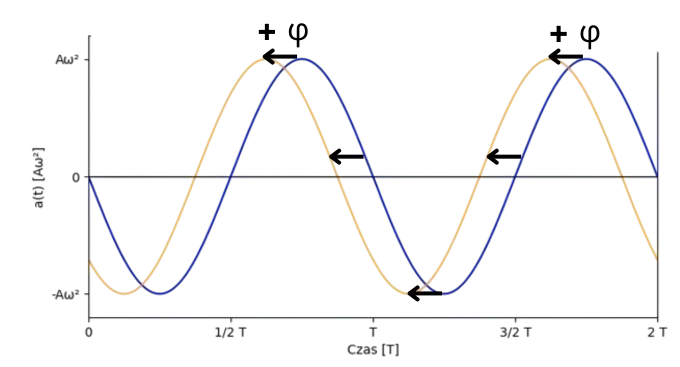
|
||
| Siła w Ruchu Harmonicznym | \( F_x = -m \cdot \omega^2 \cdot A \cdot \sin(\omega \cdot t + \phi) \) | |
Legenda Wzoru:\( F_x \) - Siła \( m \) - Masa \( A \) - Amplituda \( \omega \) - Częstość kołowa \( t \) - Czas \( \phi \) - Faza początkowa 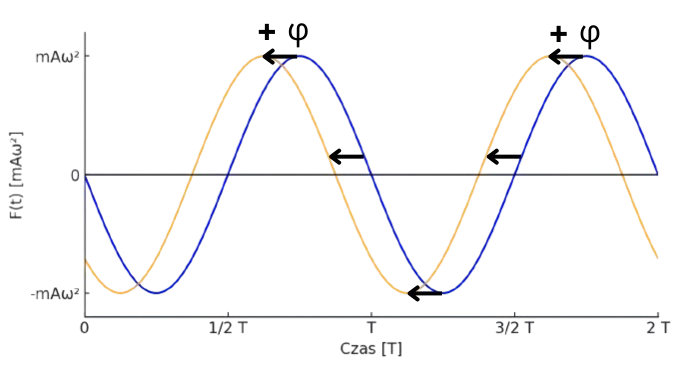
|
||
| Okres Drgań Tłumionych | \( T = \frac{2\pi}{\sqrt{\frac{k}{m} - \left(\frac{b}{2m}\right)^2}} \) | |
Legenda Wzoru:\( T \) - Okres drgań \( k \) - Stała sprężystości \( m \) - Masa \( b \) - Współczynnik tłumienia |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Okres Drgań Układu Masa-Sprężyna | \( T = 2\pi \sqrt{\frac{m}{k}} \) |
Legenda Wzoru:\( T \) - Okres drgań \( m \) - Masa \( k \) - Stała sprężystości Wyprowadzenie wzoru:1. Zależność początkowa: Zaczynamy od równania \( m \omega^2 = k \), które wiąże masę \( m \), częstotliwość kątową \( \omega \) oraz stałą sprężystości \( k \). 2. Izolacja częstotliwości kątowej: Rozwiązujemy równanie dla \( \omega^2 \), dzieląc obie strony przez \( m \): \[ \omega^2 = \frac{k}{m} \] 3. Wyznaczenie \( \omega \): Bierzemy pierwiastek z obu stron, aby znaleźć częstotliwość kątową: \[ \omega = \sqrt{\frac{k}{m}} \] 4. Okres Drgań: Okres drgań jest odwrotnością częstotliwości kątowej, co prowadzi do wzoru na okres: \[ T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{m}{k}} \] |
| Okres Drgań Wahadła Matematycznego | \( T = 2\pi \sqrt{\frac{l}{g}} \) |
Legenda Wzoru:\( T \) - Okres drgań \( l \) - Długość wahadła \( g \) - Przyspieszenie ziemskie (około 9.81 m/s²) 
Wyprowadzenie wzoru:1. Przybliżenie: Zakładamy, że kąt wychylenia \(\alpha\) jest mały, co pozwala przyjąć, że \(\sin \alpha \approx \alpha\). Wychylenie \(\alpha\) można wyrazić jako \(\frac{x}{l}\), gdzie \(x\) to przemieszczenie, a \(l\) to długość wahadła. 2. Siła Przywracająca: Siła działająca na wahadło to \( F = mg \sin \alpha \), która dla małych kątów staje się \( F = mg \frac{x}{l} \). Siła skierowana jest do położenia równowagi, więc: \[ F_x = -mg \frac{x}{l} \] 3. Równanie Ruchu: Siła sprężystości: \( F = -kx \), czyli: \[ -kx = -mg \frac{x}{l} \] z czego można wyznaczyć k: \[ k = \frac{mg}{l} \] 4. Podstawiane do wzoru: Podstawiamy wyżej wyznaczone k do wzoru, otrzymujemy \(\omega^2 = \frac{g}{l}\), więc: \[ \omega = \sqrt{\frac{g}{l}} \] co daje wzór na okres wahadła: \[ T = \frac{2\pi}{\omega} = 2\pi \sqrt{\frac{l}{g}} \] |
| Siła Sprężystości | \( F = k \cdot |x| = m \cdot \omega^2 \cdot x\) |
Legenda Wzoru:\( F \) - Siła sprężystości \( k \) - Stała sprężystości \( x \) - Wydłużenie (lub ściśnięcie) sprężyny 
Źródło: MikeRun Opis:Siła sprężystości to siła, którą sprężyna działa na ciało, gdy jest rozciągnięta lub ściśnięta o wartość \( x \). Siła ta jest proporcjonalna do wydłużenia lub skrócenia sprężyny zgodnie z prawem Hooke'a, \( F = k \cdot x \), gdzie \( k \) to stała sprężystości, a \( x \) to odległość od pozycji równowagi. |
| Współczynnik Sprężystości | \( k = -m \cdot \omega^2 = \frac{-F}{x} \) |
Legenda Wzoru:\( k \) - Stała sprężystości \( m \) - Masa układu \( \omega \) - Częstotliwość kątowa \( F \) - Siła działająca na sprężynę \( x \) - Wydłużenie sprężyny 
Źródło: MikeRun |
| Energia | ||
| Energia Potencjalna w Ruchu Harmonicznym | \( E_p = \frac{1}{2} k x^2 \) |
Legenda Wzoru:\( E_p \) - Energia potencjalna \( k \) - Stała sprężystości \( x \) - Wychylenie z położenia równowagi Opis:Energia potencjalna sprężystości to energia zgromadzona w ciele sprężystym, takim jak sprężyna, która została rozciągnięta lub ściśnięta. Zgodnie z prawem Hooke’a, energia potencjalna układu harmonicznego, np. masy na sprężynie, jest wyrażana wzorem \( E_p = \frac{1}{2} k x^2 \), gdzie \( k \) to stała sprężystości, a \( x \) to wychylenie z położenia równowagi. |
| Energia Kinetyczna w Ruchu Harmonicznym | \( E_k = \frac{1}{2} m v^2 = \frac{1}{2} m \omega^2 (A^2 - x^2) \) |
Legenda Wzoru:\( E_k \) - Energia kinetyczna \( m \) - Masa ciała \( v \) - Prędkość ciała \( \omega \) - Częstotliwość kątowa \( A \) - Amplituda drgań \( x \) - Wychylenie z położenia równowagi Opis:Energia kinetyczna w ruchu harmonicznym zależy od masy \( m \), prędkości \( v \), amplitudy drgań \( A \), oraz wychylenia \( x \). W maksymalnym wychyleniu \( x = A \) prędkość ciała wynosi 0, a energia kinetyczna jest równa 0. W punkcie równowagi \( x = 0 \) energia kinetyczna osiąga wartość maksymalną. |
| Całkowita Energia w Ruchu Harmonicznym | \( E = E_p + E_k = \frac{1}{2} k A^2 \) |
Legenda Wzoru:\( E \) - Całkowita energia układu \( E_p \) - Energia potencjalna \( E_k \) - Energia kinetyczna \( k \) - Stała sprężystości \( A \) - Amplituda drgań Opis:Całkowita energia układu harmonicznego jest sumą energii kinetycznej \( E_k \) i energii potencjalnej \( E_p \). Dla układu masy na sprężynie całkowita energia jest stała i wynosi \( E = \frac{1}{2} k A^2 \), gdzie \( A \) to amplituda, a \( k \) to stała sprężystości. |
| Wzory Ogólne | ||
| Położenie w Ruchu Harmonicznym | \(x = A \cdot \sin(\omega t + \phi)\) |
Legenda Wzoru:\(x\) - Położenie \(A\) - Amplituda \(\omega\) - Częstość kołowa \(t\) - Czas \(\phi\) - Faza początkowa 
|
| Prędkość w Ruchu Harmonicznym | \(V_x = \omega A \cdot \cos(\omega t + \phi)\) |
Legenda Wzoru:\(V_x\) - Prędkość \(A\) - Amplituda \(\omega\) - Częstość kołowa \(t\) - Czas \(\phi\) - Faza początkowa 
|
| Przyspieszenie w Ruchu Harmonicznym | \( a_x = -\omega^2 \cdot A \cdot \sin(\omega \cdot t + \phi) \) |
Legenda Wzoru:\( a_x \) - Przyspieszenie \( A \) - Amplituda \( \omega \) - Częstość kołowa \( t \) - Czas \( \phi \) - Faza początkowa 
|
| Siła w Ruchu Harmonicznym | \( F_x = -m \cdot \omega^2 \cdot A \cdot \sin(\omega \cdot t + \phi) \) |
Legenda Wzoru:\( F_x \) - Siła \( m \) - Masa \( A \) - Amplituda \( \omega \) - Częstość kołowa \( t \) - Czas \( \phi \) - Faza początkowa 
|
| Okres Drgań Tłumionych | \( T = \frac{2\pi}{\sqrt{\frac{k}{m} - \left(\frac{b}{2m}\right)^2}} \) |
Legenda Wzoru:\( T \) - Okres drgań \( k \) - Stała sprężystości \( m \) - Masa \( b \) - Współczynnik tłumienia |
Quiz - Ruch Harmoniczny
Ruch harmoniczny
Ruch harmoniczny to rodzaj drgań, w którym ciało porusza się ruchem oscylacyjnym pod wpływem siły przywracającej, która jest proporcjonalna do wychylenia ciała z położenia równowagi i skierowana w stronę tego położenia. Klasycznym przykładem jest wahadło lub masa na sprężynie.
Ruch harmoniczny charakteryzuje się okresowością, co oznacza, że wychylenie ciała zmienia się regularnie w czasie. Istnieje kilka parametrów opisujących ten ruch, takich jak okres (czas jednego pełnego cyklu), częstotliwość (ilość cykli na jednostkę czasu) i amplituda (maksymalne wychylenie z położenia równowagi).
Wzór matematyczny opisujący ruch harmoniczny to: x(t) = A cos(ωt + φ), gdzie A to amplituda, ω to częstość kołowa, a φ to faza początkowa.
Ruch harmoniczny można znaleźć w wielu systemach fizycznych, takich jak oscylatory mechaniczne, elektryczne obwody rezonansowe oraz atomy w kryształach. Zrozumienie tego rodzaju drgań jest kluczowe dla badania szerokiego zakresu zjawisk.
Drgania wymuszone pojawiają się, gdy na układ działają zewnętrzne siły, które zmuszają go do oscylacji. Kiedy częstotliwość siły wymuszającej jest bliska częstotliwości własnej układu, może dojść do zjawiska rezonansu. Rezonans to sytuacja, w której amplituda drgań gwałtownie wzrasta, co może prowadzić do dużych wychyleń i niekiedy uszkodzeń systemu.
Zjawisko rezonansu jest obserwowane w wielu obszarach, od budynków narażonych na wibracje wywołane wiatrem, po instrumenty muzyczne, w których rezonans pozwala wzmacniać dźwięki. Zrozumienie drgań wymuszonych i rezonansu jest kluczowe dla projektowania stabilnych i bezpiecznych struktur oraz urządzeń.
Drgania tłumione to rodzaj ruchu harmonicznego, w którym amplituda drgań maleje w czasie z powodu działania sił oporu, takich jak tarcie czy opór powietrza. W przeciwieństwie do drgań swobodnych, w których amplituda pozostaje stała, drgania tłumione prowadzą do stopniowego wygaszania oscylacji.
Zjawisko to można opisać równaniem: \(x(t) = A e^{-\beta t} \cos(\omega t + \phi)\), gdzie \(\beta\) to współczynnik tłumienia. Im większa wartość \(\beta\), tym szybciej amplituda drgań maleje. Drgania tłumione są powszechnie obserwowane w różnych systemach, takich jak wahadła z tłumieniem, systemy sprężynowe z oporem oraz w wielu obszarach inżynierii mechanicznej.
Zrozumienie drgań tłumionych jest istotne w projektowaniu urządzeń i konstrukcji, ponieważ nadmierne drgania mogą prowadzić do uszkodzeń lub obniżenia wydajności systemu. Przykłady zastosowań obejmują amortyzatory w pojazdach oraz systemy kontrolujące drgania w budynkach.
Podsumowując, ruch harmoniczny, drgania wymuszone, rezonans oraz drgania tłumione to podstawowe pojęcia związane z teorią drgań, które mają szerokie zastosowanie w fizyce i inżynierii.