Wzory termodynamika
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Pierwsza Zasada Termodynamiki | \( \Delta U = Q + W_z \) | |
|
Jednostka Energi Wewnętrznej (\( \Delta U \)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\( \Delta U \) - Zmiana energii wewnętrznej \( Q \) - Ciepło dostarczone do układu \( W_z \) - Praca wykonana nad gazem przez siłę zewnętrzną |
||
| Równanie Stanu Gazów Doskonałych | \( PV = nRT \) | |
|
Jednostka Stałej Gazowej (\( R \)): 8.314 \(J/(mol \cdot K)\) Legenda Wzoru:\( P \) - Ciśnienie \( V \) - Objętość \( n \) - Liczba moli \( R \) - Stała gazowa \( T \) - Temperatura w kelwinach |
||
| Energia wewnętrzna | \( U = \frac{i}{2} k N T \) | |
Legenda Wzoru:\( U \) - Energia wewnętrzna \( i \) - Liczba stopni swobody \( k \) - Stała Boltzmanna \( N \) - Liczba cząstek \( T \) - Temperatura Opis:
Energia wewnętrzna jest miarą całkowitej energii termicznej układu, zależnej od liczby stopni swobody, temperatury oraz stałej Boltzmanna. |
||
| Ciepło | ||
| Wymiana ciepła - stała objętość | \( Q_v = c_v m \Delta T = C_v \cdot n \Delta T \) | |
Legenda Wzoru:\( Q_v \) - Przemiana ciepła przy stałej objętości \( c_v \) - Ciepło właściwe przy stałej objętości (na jednostkę masy) \( C_v \) - Ciepło molowe przy stałej objętości \( m \) - Masa \( n \) - Liczba moli \( \Delta T \) - Zmiana temperatury Opis:
Wzór opisuje ilość ciepła wymienianego w procesie przy stałej objętości, gdzie \( c_v \) jest ciepłem właściwym na jednostkę masy, a \( C_v \) jest ciepłem molowym przy stałej objętości. |
||
| Wymiana ciepła - stałe ciśnienie | \( Q_p = c_p m \Delta T = C_p \cdot n \Delta T \) | |
Legenda Wzoru:\( Q_p \) - Przemiana ciepła przy stałym ciśnieniu \( c_p \) - Ciepło właściwe przy stałym ciśnieniu (na jednostkę masy) \( C_p \) - Ciepło molowe przy stałym ciśnieniu \( m \) - Masa \( n \) - Liczba moli \( \Delta T \) - Zmiana temperatury Opis:
Wzór opisuje ilość ciepła wymienianego w procesie przy stałym ciśnieniu, gdzie \( c_p \) jest ciepłem właściwym na jednostkę masy, a \( C_p \) jest ciepłem molowym przy stałym ciśnieniu. |
||
| Praca | ||
| Praca przy przemianie izobarycznej | \( W = p \Delta V \) | |
Legenda Wzoru:\( W \) - Praca \( p \) - Ciśnienie \( \Delta V \) - Zmiana objętości 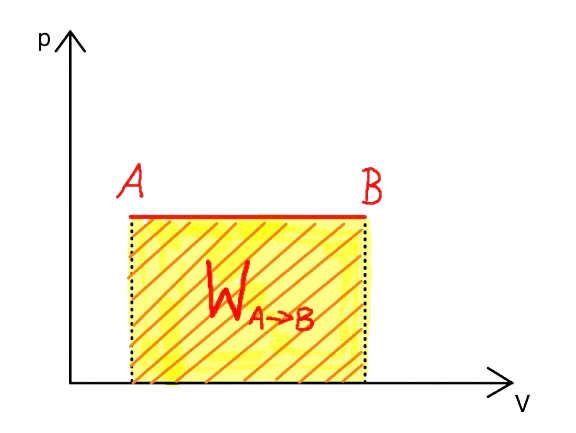
Opis:
Wzór opisuje pracę wykonaną przez gaz lub nad gazem podczas przemiany izobarycznej, czyli przy stałym ciśnieniu. |
||
| Praca (wzór ogólny) | \( W = \int_{V_i}^{V_f} p \, dV \) (Pole pod wykresem \( p(V) \) ) | |
Legenda Wzoru:\( W \) - Praca \( p \) - Ciśnienie \( V_i \) - Początkowa objętość \( V_f \) - Końcowa objętość 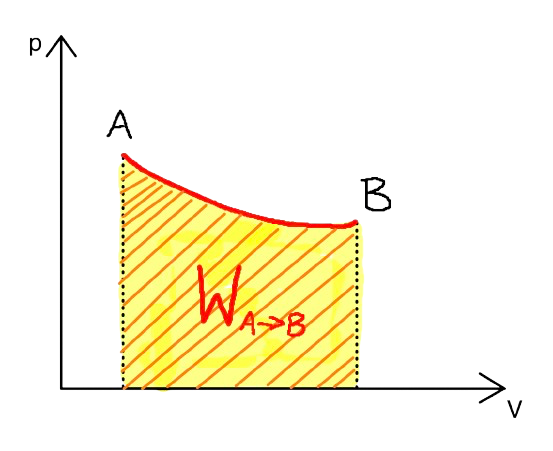
Opis:
Wzór opisuje pracę wykonaną przez gaz lub nad gazem podczas przemiany, w której ciśnienie zmienia się w zależności od objętości. Praca w tym przypadku równa jest polu pod wykresem ciśnienia \( P \) w funkcji objętości \( V \). |
||
| Sprawność | ||
| Sprawność Silnika Carnota | \(\eta = \frac{Q_{pobr} - Q_{odd}}{Q_{pobr}}, \eta = 1 - \frac{T_C}{T_H}\) | |
Legenda Wzoru:\( \eta \) - Sprawność \( T_C \) - Temperatura chłodnicy \( T_H \) - Temperatura grzejnika \( Q_{pobr} \) - Ciepło pobrane \( Q_{odd} \) - Ciepło oddane 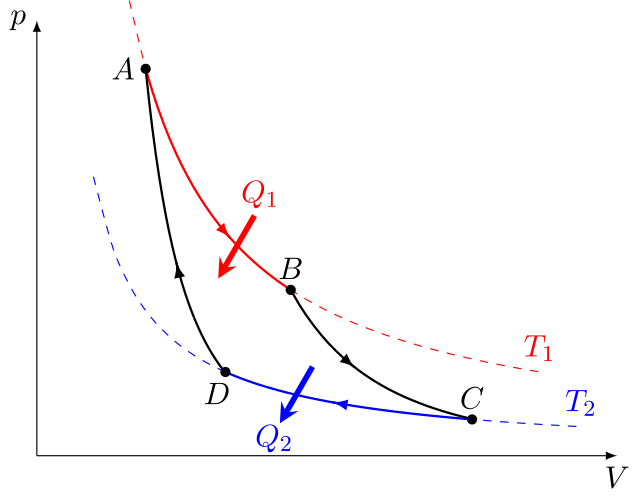
Opis:
Sprawność silnika Carnota jest maksymalną możliwą sprawnością, jaką można uzyskać w silniku cieplnym operującym między dwoma temperaturami. Druga formuła opisuje stosunek ciepła pobranego do ciepła oddanego, co jest istotne w kontekście analizy efektywności silnika. |
||
| Skuteczność chłodzenia | \( \varepsilon = \frac{Q}{W} = \frac{T_2}{T_1 - T_2} \) | |
Legenda Wzoru:\( \varepsilon \) - Skuteczność chłodzenia \( Q \) - Ciepło pobrane odchłodzonego pomieszczenia \( W \) - Praca wykonana podczas pompowania ciepła (z chłodniejszego pomieszczenia do cieplejszego ciała) \( T_1 \) - Temperatura ciała, do którego oddawane jest ciepło z pomieszczenia \( T_2 \) - Temperatura chłodzonego pomieszczenia Opis:
Skuteczność chłodzenia określa stosunek odprowadzonego ciepła do dostarczonego ciepła w procesie chłodzenia. |
||
| Inne | ||
| Równanie Clausiusa-Clapeyrona | \( \frac{dP}{dT} = \frac{L}{T(V_2 - V_1)} \) | |
Legenda Wzoru:\( dP \) - Zmiana ciśnienia \( dT \) - Zmiana temperatury \( L \) - Ciepło parowania \( V_1 \) - Objętość cieczy \( V_2 \) - Objętość gazu Opis:
Równanie Clausiusa-Clapeyrona opisuje zależność między temperaturą a ciśnieniem podczas przemiany fazowej. |
||
| Entropia | \( \Delta S = \frac{Q_{rev}}{T} \) | |
Legenda Wzoru:\( \Delta S \) - Zmiana entropii \( Q_{rev} \) - Ciepło wymienione w procesie odwracalnym \( T \) - Temperatura Opis:
Entropia jest miarą stopnia nieuporządkowania układu. Zmiana entropii określa, jak zmienia się ten stopień podczas wymiany ciepła. |
||
| Średnia energia kinetyczna ruchu postępowego cząstki gazu | \( \langle E_k \rangle = \frac{3}{2} k_B T \) | |
Legenda Wzoru:\( \langle E_k \rangle \) - Średnia energia kinetyczna \( k_B \) - Stała Boltzmanna \( T \) - Temperatura w kelwinach Opis:
Wzór ten opisuje średnią energię kinetyczną cząstki gazu doskonałego, która jest proporcjonalna do temperatury gazu. |
||
| Ciśnienie gazów | \( p = \frac{2}{3} \frac{N}{V} \langle E_k \rangle \) | |
Legenda Wzoru:\( p \) - Ciśnienie \( N \) - Liczba cząstek \( V \) - Objętość \( \langle E_k \rangle \) - Średnia energia kinetyczna Opis:
Wzór opisuje ciśnienie gazu idealnego w kontekście jego średniej energii kinetycznej. |
||
| Stała Boltzmanna | \( k = \frac{R}{N_A} \) | |
Legenda Wzoru:\( k \) - Stała Boltzmanna \( R \) - Stała gazowa \( N_A \) - Liczba Avogadra Opis:
Stała Boltzmanna jest proporcjonalna do stałej gazowej i liczby Avogadra, używana w mechanice statystycznej do opisu rozkładu statystycznego cząstek w gazach. |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Pierwsza Zasada Termodynamiki | \( \Delta U = Q + W_z \) |
Jednostka Energi Wewnętrznej (\( \Delta U \)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\( \Delta U \) - Zmiana energii wewnętrznej \( Q \) - Ciepło dostarczone do układu \( W_z \) - Praca wykonana nad gazem przez siłę zewnętrzną |
| Równanie Stanu Gazów Doskonałych | \( PV = nRT \) |
Jednostka Stałej Gazowej (\( R \)): 8.314 \(J/(mol \cdot K)\) Legenda Wzoru:\( P \) - Ciśnienie \( V \) - Objętość \( n \) - Liczba moli \( R \) - Stała gazowa \( T \) - Temperatura w kelwinach |
| Energia wewnętrzna | \( U = \frac{i}{2} k N T \) |
Legenda Wzoru:\( U \) - Energia wewnętrzna \( i \) - Liczba stopni swobody \( k \) - Stała Boltzmanna \( N \) - Liczba cząstek \( T \) - Temperatura Energia wewnętrzna jest miarą całkowitej energii termicznej układu, zależnej od liczby stopni swobody, temperatury oraz stałej Boltzmanna. |
| Ciepło | ||
| Wymiana ciepła - stała objętość | \( Q_v = c_v m \Delta T = C_v \cdot n \Delta T \) |
Legenda Wzoru:\( Q_v \) - Przemiana ciepła przy stałej objętości \( c_v \) - Ciepło właściwe przy stałej objętości (na jednostkę masy) \( C_v \) - Ciepło molowe przy stałej objętości \( m \) - Masa \( n \) - Liczba moli \( \Delta T \) - Zmiana temperatury Wzór opisuje ilość ciepła wymienianego w procesie przy stałej objętości, gdzie \( c_v \) jest ciepłem właściwym na jednostkę masy, a \( C_v \) jest ciepłem molowym przy stałej objętości. |
| Wymiana ciepła - stałe ciśnienie | \( Q_p = c_p m \Delta T = C_p \cdot n \Delta T \) |
Legenda Wzoru:\( Q_p \) - Przemiana ciepła przy stałym ciśnieniu \( c_p \) - Ciepło właściwe przy stałym ciśnieniu (na jednostkę masy) \( C_p \) - Ciepło molowe przy stałym ciśnieniu \( m \) - Masa \( n \) - Liczba moli \( \Delta T \) - Zmiana temperatury Wzór opisuje ilość ciepła wymienianego w procesie przy stałym ciśnieniu, gdzie \( c_p \) jest ciepłem właściwym na jednostkę masy, a \( C_p \) jest ciepłem molowym przy stałym ciśnieniu. |
| Praca | ||
| Praca przy przemianie izobarycznej | \( W = p \Delta V \) |
Legenda Wzoru:\( W \) - Praca \( p \) - Ciśnienie \( \Delta V \) - Zmiana objętości 
Opis:
Wzór opisuje pracę wykonaną przez gaz lub nad gazem podczas przemiany izobarycznej, czyli przy stałym ciśnieniu. |
| Praca przy przemianie nieizobarycznej | \( W = \int_{V_i}^{V_f} p \, dV \) |
Legenda Wzoru:\( W \) - Praca \( p \) - Ciśnienie \( V_i \) - Początkowa objętość \( V_f \) - Końcowa objętość 
Opis:
Wzór opisuje pracę wykonaną przez gaz lub nad gazem podczas przemiany, w której ciśnienie zmienia się w zależności od objętości. Praca w tym przypadku równa jest polu pod wykresem ciśnienia \( P \) w funkcji objętości \( V \). |
| Sprawność | ||
| Sprawność Silnika Carnota | \( \eta = 1 - \frac{T_C}{T_H}, \eta = \frac{Q_{pobr} - Q_{odd}}{Q_{pobr}} \) |
Legenda Wzoru:\( \eta \) - Sprawność \( T_C \) - Temperatura chłodnicy \( T_H \) - Temperatura grzejnika \( Q_{pobr} \) - Ciepło pobrane \( Q_{odd} \) - Ciepło oddane 
Sprawność silnika Carnota jest maksymalną możliwą sprawnością, jaką można uzyskać w silniku cieplnym operującym między dwoma temperaturami. |
| Skuteczność chłodzenia | \( \varepsilon = \frac{Q_{ch}}{Q_{we}} = \frac{T_{ch} - T_{we}}{T_{ch}} \) |
Legenda Wzoru:\( \varepsilon \) - Skuteczność chłodzenia \( Q \) - Ciepło pobrane odchłodzonego pomieszczenia \( W \) - Praca wykonana podczas pompowania ciepła (z chłodniejszego pomieszczenia do cieplejszego ciała) \( T_1 \) - Temperatura ciała, do którego oddawane jest ciepło z pomieszczenia \( T_2 \) - Temperatura chłodzonego pomieszczenia Opis:
Skuteczność chłodzenia określa stosunek odprowadzonego ciepła do dostarczonego ciepła w procesie chłodzenia. |
| Inne | ||
| Równanie Clausiusa-Clapeyrona | \( \frac{dP}{dT} = \frac{L}{T(V_2 - V_1)} \) |
Legenda Wzoru:\( dP \) - Zmiana ciśnienia \( dT \) - Zmiana temperatury \( L \) - Ciepło parowania \( V_1 \) - Objętość cieczy \( V_2 \) - Objętość gazu Równanie Clausiusa-Clapeyrona opisuje zależność między temperaturą a ciśnieniem podczas przemiany fazowej. |
| Entropia | \( \Delta S = \frac{Q_{rev}}{T} \) |
Legenda Wzoru:\( \Delta S \) - Zmiana entropii \( Q_{rev} \) - Ciepło wymienione w procesie odwracalnym \( T \) - Temperatura Entropia jest miarą stopnia nieuporządkowania układu. Zmiana entropii określa, jak zmienia się ten stopień podczas wymiany ciepła. |
| Średnia energia kinetyczna ruchu postępowego cząstki gazu | \( \langle E_k \rangle = \frac{3}{2} k_B T \) |
Legenda Wzoru:\( \langle E_k \rangle \) - Średnia energia kinetyczna \( k_B \) - Stała Boltzmanna \( T \) - Temperatura w kelwinach Wzór ten opisuje średnią energię kinetyczną cząstki gazu doskonałego, która jest proporcjonalna do temperatury gazu. |
| Ciśnienie gazów | \( p = \frac{2}{3} \frac{N}{V} \langle E_k \rangle \) |
Legenda Wzoru:\( p \) - Ciśnienie \( N \) - Liczba cząstek \( V \) - Objętość \( \langle E_k \rangle \) - Średnia energia kinetyczna Wzór opisuje ciśnienie gazu idealnego w kontekście jego średniej energii kinetycznej. |
| Stała Boltzmanna | \( k = \frac{R}{N_A} \) |
Legenda Wzoru:\( k \) - Stała Boltzmanna \( R \) - Stała gazowa \( N_A \) - Liczba Avogadra Stała Boltzmanna jest proporcjonalna do stałej gazowej i liczby Avogadra, używana w mechanice statystycznej do opisu rozkładu statystycznego cząstek w gazach. |
Quiz - Termodynamika
Termodynamika
Termodynamika jest działem fizyki zajmującym się badaniem procesów cieplnych i przemian energii. Obejmuje badania nad ciepłem, pracą, temperaturą oraz ich związkami z energią i materią.
Termodynamika opiera się na czterech podstawowych zasadach, które określają sposób przemiany energii w różnych systemach fizycznych. Pierwsza zasada termodynamiki, znana również jako zasada zachowania energii, mówi, że energia nie może być ani stworzona, ani zniszczona, jedynie przemieniona z jednej formy w drugą.
Druga zasada termodynamiki wprowadza pojęcie entropii, miary nieuporządkowania układu, i stwierdza, że entropia wszechświata zawsze wzrasta w procesach naturalnych. Trzecia zasada termodynamiki mówi, że entropia kryształu doskonałego w temperaturze zera absolutnego wynosi zero.
Termodynamika ma szerokie zastosowanie w różnych dziedzinach nauki i techniki, takich jak inżynieria, chemia, biologia, meteorologia i wiele innych. Zrozumienie procesów termodynamicznych jest kluczowe dla projektowania silników, chłodziarek, elektrowni i wielu innych urządzeń.
Badania w termodynamice umożliwiają przewidywanie, jak energia cieplna będzie przemieszczać się między systemami, co jest niezbędne dla rozwoju efektywnych systemów energetycznych. Termodynamika jest również związana z kinetyką chemiczną, analizą procesów przemysłowych oraz zrozumieniem zjawisk atmosferycznych.
Zainteresowanie termodynamiką jest istotne zarówno dla naukowców, inżynierów, jak i osób zainteresowanych fizyką oraz technikami wykorzystującymi energię cieplną w różnych procesach i urządzeniach.
Podsumowując, termodynamika jest dziedziną fizyki zajmującą się przemianami energii i ciepła, mającą szerokie zastosowanie praktyczne oraz kluczowe znaczenie dla zrozumienia procesów zachodzących w przyrodzie i technice.