Wzory bryła sztywna
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Moment Pędu | \(L = I \cdot \omega = m \cdot v \cdot r\) | |
Legenda Wzoru:\(L\) - Moment Pędu \(I\) - Moment Bezwładności \(\omega\) - Prędkość Kątowa \(m\) - Masa obiektu \(v\) - Prędkość liniowa \(r\) - Promień (odległość od osi obrotu) 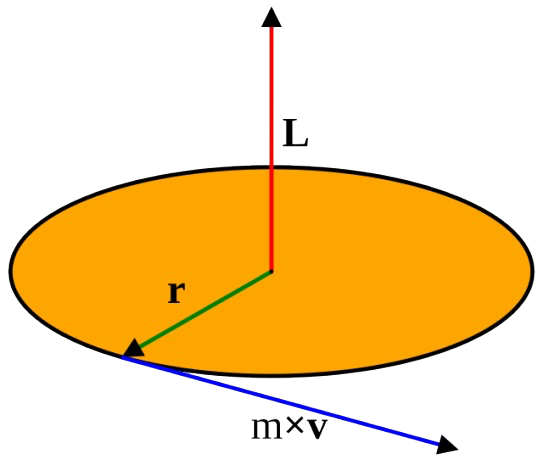
|
||
| Moment Siły | \( M = F \cdot d \cdot \sin(\alpha) = \epsilon \cdot I^* \) | |
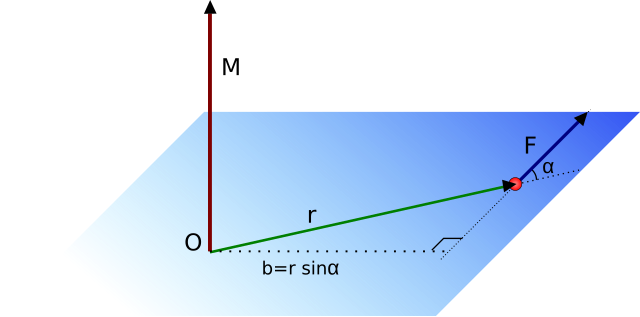
Legenda Wzoru:\( M \) - Moment Siły \( F \) - Siła \( d \) - Odległość od Osi Obracania do Punktów Działania Siły \( \alpha \) - Kąt między Siłą a Wektorem Odległości \( \epsilon \) - Przyspieszenie Kątowe \( ^* \) Wzór stosowany dla wypadkowego momentu siły. |
||
| Prędkość Kątowa | \(\omega = \frac{v}{r}\ = \frac{2\pi n}{t}\ = \frac{2\pi}{T} = 2\pi f = \frac{\Delta \alpha}{t}\) | |
Legenda Wzoru:\(\omega\) - Prędkość Kątowa \(v\) - Prędkość Liniowa \(r\) - Promień Krzywizny Trasy \(n\) - Liczba Obrotów na Sekundę \(t\) - Czas \(T\) - Okres Obrotu \(f\) - Częstotliwość Obrotowa \(\Delta \alpha\) - Kąt Obrotu |
||
| Przyśpieszenie Kątowe | \(\epsilon= \frac{a}{r}\ = \frac{\Delta \omega}{\Delta t}\) | |
Legenda Wzoru:\(\epsilon\) - Przyspieszenie Kątowe \(a\) - Przyspieszenie Liniowe \(r\) - Promień Krzywizny Trasy \(\Delta \omega\) - Zmiana Prędkości Kątowej \(\Delta t\) - Zmiana Czasu |
||
| Energia kinetyczna ruchu obrotowego | \( E_{k_{\text{obr}}} = \frac{1}{2} I \omega^2 \) | |
|
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_{k_{\text{obr}}}\) - Energia kinetyczna ruchu obrotowego \(I\) - Moment bezwładności \( \omega \) - Prędkość kątowa |
||
| Momenty Bezwładności Ciał | (Rozwiń opis) | |
Legenda Wzoru:Momenty Bezwładności różnych ciał względem ich osi symetrii: • Kula: \( \frac{2}{5} m R^2 \) • Sfera: \( \frac{2}{3} m R^2 \) • Walec: \( \frac{1}{2} m R^2 \) • Cienkościennej rura: \( m R^2 \) • Pełny krążek: \( \frac{1}{2} m R^2 \) • Cienkiego pierścienia: \( m R^2 \) • Pręt: \( \frac{1}{12} m L^2 \) |
||
| Twierdzenie Steinera | \(I_2 = I_o + m \cdot d^2 \) | |
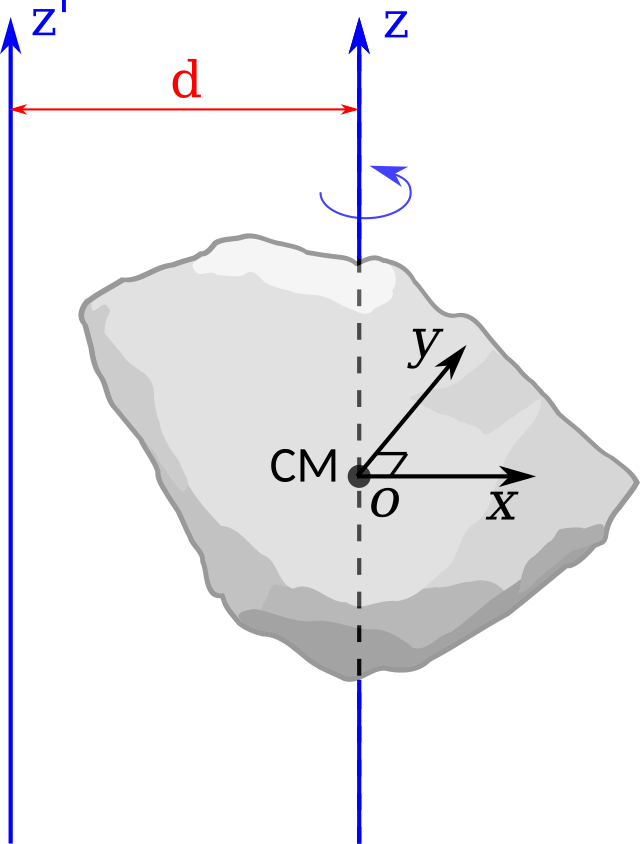
Legenda Wzoru:\(I_2 = I_o + m \cdot d^2 \) \( I_o\) - Moment bezwładności względem względem którejś z osi symetrii ciała \( d\) - Odległość pomiędzy osiami obrotu Moment bezwładności względem dowolnej osi \( O_2 \), równoległej do osi \( O \) która jest osią symetrii bryły, można obliczyć za pomocą twierdzenia Steinera. Jest to jedno z kluczowych narzędzi w analizie ruchu obrotowego, pozwalające nam wyznaczyć momenty bezwładności dla różnych osi, co ma istotne znaczenie w mechanice i inżynierii. |
Równia pochyła | |
| Przyśpieszenie Bryły Sztywnej na Równi bez Poślizgu* | \(a = \frac{g \cdot \sin(\alpha)}{1 + \frac{I}{mR^2}}\) | |
Legenda Wzoru:\(a\) - Przyspieszenie \(g\) - Przyspieszenie Ziemskie \(\alpha\) - Kąt Nachylenia Równi \(I\) - Moment Bezwładności \(m\) - Masa \(R\) - Promień Wyprowadzenie Wzoru: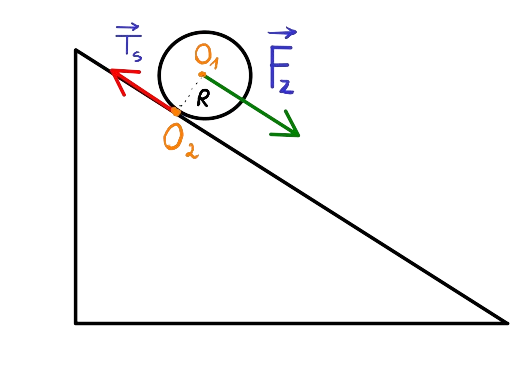
Gdzie:
Sposób 1:Rozwiązanie poniższego układu równań dynamiki dla osi obrotu ciała znajdującej się w środku masy: 
Sposób 2:Rozwiązanie poniższego układu równań dynamiki dla osi chwilowej, znajdującej się w miejscu kontaktu ciała z równią: 
|
||
| Prędkość Liniowa Bryły po Stoczeniu z Równi | \(v = \sqrt{\frac{2 \cdot g \cdot (h_p - h_k)}{1 + \frac{I}{mR^2}}}\) | |
Legenda Wzoru:\(v\) - Prędkość Liniowa \(g\) - Przyspieszenie Ziemskie \(h_p\) - Wysokość Początkowa \(h_k\) - Wysokość Końcowa \(I\) - Moment Bezwładności \(m\) - Masa \(R\) - Promień Wyprowadzenie wzoru:
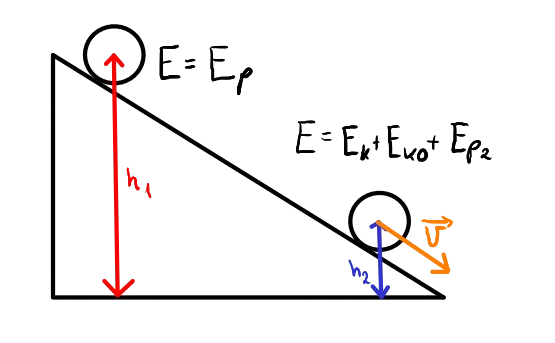
Gdzie:
Korzystamy z zasady zachowania energii. Energia początkowa ciała będzie równała się końcowej energii ciała. Na początku ciało spoczywa, więc posiada tylko energię potencjalną, z czasem jednak energia potencjalna stopniowo zmienia się na kinetyczną oraz energię kinetyczną obrotową. Wzór na energię potencjalną: \( m \cdot g \cdot h \) Wzór na energię kinetyczną: \( \frac{m \cdot v^2}{2} \) Wzór na energię kinetyczną obrotową: \( \frac{I \cdot \omega^2}{2} \) Zapisujemy więc układ równań:
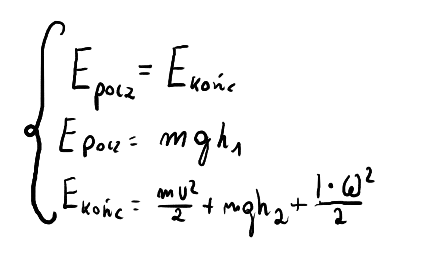
Gdzie:
|
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Moment Pędu | \(L = I \cdot \omega = m \cdot v \cdot r\) |
Legenda Wzoru:\(L\) - Moment Pędu \(I\) - Moment Bezwładności \(\omega\) - Prędkość Kątowa \(m\) - Masa obiektu \(v\) - Prędkość liniowa \(r\) - Promień (odległość od osi obrotu) 
|
| Moment Siły | \( M = F \cdot d \cdot \sin(\alpha) = \epsilon \cdot I^* \) |

Legenda Wzoru:\( M \) - Moment Siły \( F \) - Siła \( d \) - Odległość od Osi Obracania do Punktów Działania Siły \( \alpha \) - Kąt między Siłą a Wektorem Odległości \( \epsilon \) - Przyspieszenie Kątowe \( I \) - Moment Bezwładności \( ^* \) Wzór stosowany dla wypadkowego momentu siły. |
| Prędkość Kątowa | \(\omega = \frac{v}{r}\ = \frac{2\pi n}{t}\ = \frac{2\pi}{T} = 2\pi f = \frac{\Delta \alpha}{t}\) |
Legenda Wzoru:\(\omega\) - Prędkość Kątowa \(v\) - Prędkość Liniowa \(r\) - Promień Krzywizny Trasy \(n\) - Liczba Obrotów na Sekundę \(t\) - Czas \(T\) - Okres Obrotu \(f\) - Częstotliwość Obrotowa \(\Delta \alpha\) - Kąt Obrotu |
| Energia kinetyczna ruchu obrotowego | \( E_{k_{\text{obr}}} = \frac{1}{2} I \omega^2 \) |
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_{k_{\text{obr}}}\) - Energia kinetyczna ruchu obrotowego \(I\) - Moment bezwładności \( \omega \) - Prędkość kątowa |
| Przyśpieszenie Kątowe | \(\epsilon= \frac{a}{r}\ = \frac{\Delta \omega}{\Delta t}\) |
Legenda Wzoru:\(\epsilon\) - Przyspieszenie Kątowe \(a\) - Przyspieszenie Liniowe \(r\) - Promień Krzywizny Trasy \(\Delta \omega\) - Zmiana Prędkości Kątowej \(\Delta t\) - Zmiana Czasu |
| Momenty Bezwładności Ciał | (Rozwiń opis) |
Momenty Bezwładności różnych ciał względem ich osi symetrii::• Kula: \( \frac{2}{5} m R^2 \) • Sfera: \( \frac{2}{3} m R^2 \) • Walec: \( \frac{1}{2} m R^2 \) • Cienkościennej rura: \( m R^2 \) • Pełny krążek: \( \frac{1}{2} m R^2 \) • Cienkiego pierścienia: \( m R^2 \) • Pręt: \( \frac{1}{12} m L^2 \) |
| Twierdzenie Steinera | \(I_2 = I_o + m \cdot d^2 \) |

Legenda Wzoru:\(I_2 = I_o + m \cdot d^2 \) \( I_o\) - Moment bezwładności względem względem którejś z osi symetrii ciała \( d\) - Odległość pomiędzy osiami obrotu Moment bezwładności względem dowolnej osi \( O_2 \), równoległej do osi \( O \) która jest osią symetrii bryły, można obliczyć za pomocą twierdzenia Steinera. Jest to jedno z kluczowych narzędzi w analizie ruchu obrotowego, pozwalające nam wyznaczyć momenty bezwładności dla różnych osi, co ma istotne znaczenie w mechanice i inżynierii. |
| Równia Pochyła | ||
| Przyśpieszenie Bryły Sztywnej na Równi bez Poślizgu* | \(a = \frac{g \cdot \sin(\alpha)}{1 + \frac{I}{mR^2}}\) |
Legenda Wzoru:\(a\) - Przyspieszenie \(g\) - Przyspieszenie Ziemskie \(\alpha\) - Kąt Nachylenia Równi \(I\) - Moment Bezwładności \(m\) - Masa \(R\) - Promień Wyprowadzenie Wzoru:
Gdzie:
Sposób 1:Rozwiązanie poniższego układu równań dynamiki dla osi obrotu ciała znajdującej się w środku masy: 
Sposób 2:Rozwiązanie poniższego układu równań dynamiki dla osi chwilowej, znajdującej się w miejscu kontaktu ciała z równią: 
|
| Prędkość Liniowa Bryły po Stoczeniu z Równi | \(v = \sqrt{\frac{2 \cdot g \cdot (h_p - h_k)}{1 + \frac{I}{mR^2}}}\) |
Legenda Wzoru:\(v\) - Prędkość Liniowa \(g\) - Przyspieszenie Ziemskie \(h_p\) - Wysokość Początkowa \(h_k\) - Wysokość Końcowa \(I\) - Moment Bezwładności \(m\) - Masa \(R\) - Promień Wyprowadzenie wzoru:

Gdzie:
Korzystamy z zasady zachowania energii. Energia początkowa ciała będzie równała się końcowej energii ciała. Na początku ciało spoczywa, więc posiada tylko energię potencjalną, z czasem jednak energia potencjalna stopniowo zmienia się na kinetyczną oraz energię kinetyczną obrotową. Wzór na energię potencjalną: \( m \cdot g \cdot h \) Wzór na energię kinetyczną: \( \frac{m \cdot v^2}{2} \) Wzór na energię kinetyczną obrotową: \( \frac{I \cdot \omega^2}{2} \) Zapisujemy więc układ równań: 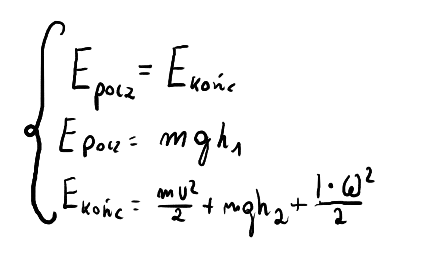
Gdzie:
|
Quiz - Bryła Sztywna
Bryła Sztywna
Bryła sztywna, w kontekście fizyki, jest to idealizacja ciała fizycznego, w którym elementy składowe są nieruchome względem siebie. Jest to układ wielu punktów materialnych, których wzajemne odległości pozostają stałe. Rozkład masy w obrębie bryły jest opisywany przez różne parametry, takie jak środek masy oraz moment bezwładności. Bryła sztywna stanowi model, który umożliwia analizę ruchu i zachowania obiektów fizycznych.
Środek masy, w kontekście brył sztywnych i układów punktów materialnych, jest istotnym pojęciem w fizyce. Jest to punkt geometryczny, który reprezentuje średnie położenie masy całego obiektu lub układu punktów materialnych.
Definicja środka masy mówi, że jest to punkt, w którym można zlokalizować całą masę obiektu, tak aby zachowana była równowaga momentów względem dowolnego punktu. W przypadku układów punktów materialnych, środek masy reprezentuje średnie położenie masy całego układu.
W przypadku brył sztywnych o jednorodnej gęstości, środek masy pokrywa się ze środkiem geometrycznym bryły. Na przykład, środek masy kuli znajduje się w jej środku, a środek masy odcinka znajduje się w jego połowie.
W przypadku brył sztywnych o nierównomiernym rozkładzie masy, środek masy może być przesunięty względem środka geometrycznego. W takich przypadkach środek masy jest obliczany przy użyciu odpowiednich metod matematycznych, uwzględniając rozkład masy wewnątrz bryły.
Środek masy jest istotnym pojęciem w analizie ruchu i równowagi obiektów fizycznych. Umożliwia precyzyjne opisanie zachowania obiektów pod wpływem sił zewnętrznych oraz umożliwia analizę dynamiki układów złożonych.
Zrozumienie położenia środka masy jest kluczowe w projektowaniu konstrukcji, maszyn, pojazdów oraz w analizie biomechanicznej ciała ludzkiego. Pomaga to w zapewnieniu stabilności, wytrzymałości i bezpieczeństwa różnych struktur i urządzeń.