| Kategoria | Wzór | Opis Wzoru | Siła i Pęd |
|---|---|---|
| Siła | \(F = m \cdot a = \frac{\Delta p}{\Delta t}\) | |
Legenda Wzoru:\(F\) - Siła \(m\) - Masa \(a\) - Przyspieszenie \(p\) - Pęd \(\Delta p\) - Zmiana pędu \(\Delta t\) - Zmiana czasu |
||
| Pęd | \(p = F \cdot t = m \cdot a \cdot t = m \cdot v\) | |
Legenda Wzoru:\(p\) - Pęd \(F\) - Siła \(t\) - Czas \(m\) - Masa \(a\) - Przyspieszenie \(v\) - Prędkość |
||
| Zasada zachowania pędu | \(p_{c1} = p_{c2}, \quad \vec{p_1} + \vec{p_2} = \vec{p_1'} + \vec{p_2'}\) | |
Legenda Wzoru:\(p_{c1}\) - Całkowity pęd układu przed zderzeniem \(p_{c2}\) - Całkowity pęd układu po zderzeniu \(\vec{p_1}\) - Pęd pierwszego ciała przed zderzeniem \(\vec{p_2}\) - Pęd drugiego ciała przed zderzeniem \(\vec{p_1'}\) - Pęd pierwszego ciała po zderzeniu \(\vec{p_2'}\) - Pęd drugiego ciała po zderzeniu Całkowity pęd układu przed zderzeniem (\(p_{c1}\)) jest równy całkowitemu pędowi układu po zderzeniu (\(p_{c2}\)) zgodnie z zasadą zachowania pędu. Sumy wektorowe: \(\vec{p_1} + \vec{p_2} = \vec{p_1'} + \vec{p_2'}\) uwzględniają kierunek i wartość pędów. |
Rodzaje Sił | |
| Siła Tarcia Statycznego | \(F_{t_s} = N \cdot \mu_s\) | |
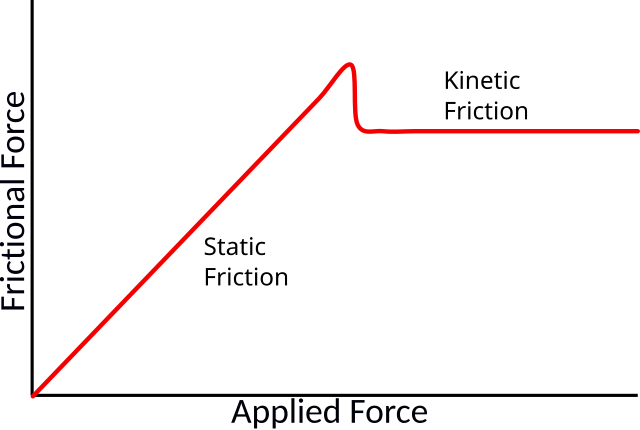
Legenda Wzoru:\(F_{t_s}\) - Siła Tarcia Statycznego \(N\) - Siła Normalna \(\mu_s\) - Współczynnik Tarcia Statycznego Opis:Siła tarcia statycznego występuje, gdy przedmiot znajduje się w spoczynku i przeciwstawia się rozpoczęciu ruchu. Jest to największa siła tarcia, która działa na ciało, zanim zacznie ono się poruszać. Aby przesunąć obiekt z miejsca, siła działająca na niego musi przekroczyć siłę tarcia statycznego. |
||
| Siła Tarcia Kinetycznego | \(F_{t_k} = N \cdot \mu_k\) | |
Legenda Wzoru:\(F_{t_k}\) - Siła Tarcia Kinetycznego \(N\) - Siła Normalna \(\mu_k\) - Współczynnik Tarcia Kinetycznego Opis:Siła tarcia kinetycznego działa, gdy przedmiot jest już w ruchu. W porównaniu do siły tarcia statycznego, tarcie kinetyczne jest mniejsze, co oznacza, że po ruszeniu przedmiotu potrzeba mniejszej siły, aby utrzymać go w ruchu. Z tego powodu łatwiej jest przesuwać obiekt, gdy jest już w ruchu, niż rozpocząć jego ruch. |
||
| Siła Dośrodkowa | \(F_d = m \cdot \frac{v^2}{r}\) | |
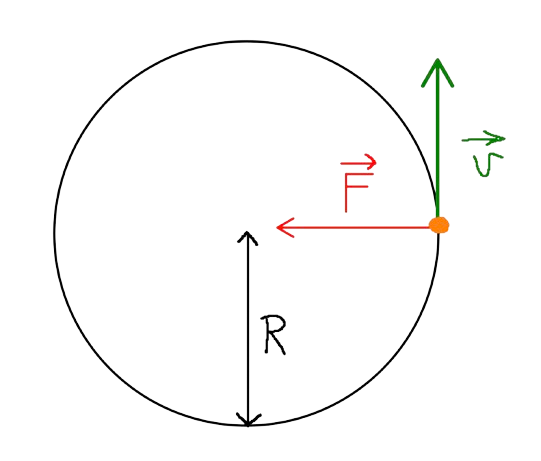
Legenda Wzoru:\(F_d\) - Siła Dośrodkowa \(m\) - Masa ciała \(v\) - Prędkość \(r\) - Promień Krzywizny Trasy |
||
| Siła Ciężkości | \(F = m \cdot g\) | |
Legenda Wzoru:\(F\) - Siła Ciężkości \(m\) - Masa ciała \(g\) - Przyspieszenie ziemskie (około 9.81 m/s²) |
Równia Pochyła | |
| Przyśpieszenie na Równi Pochyłej | \(a = g \cdot \sin(\alpha)\) | |
Wyprowadzenie wzoru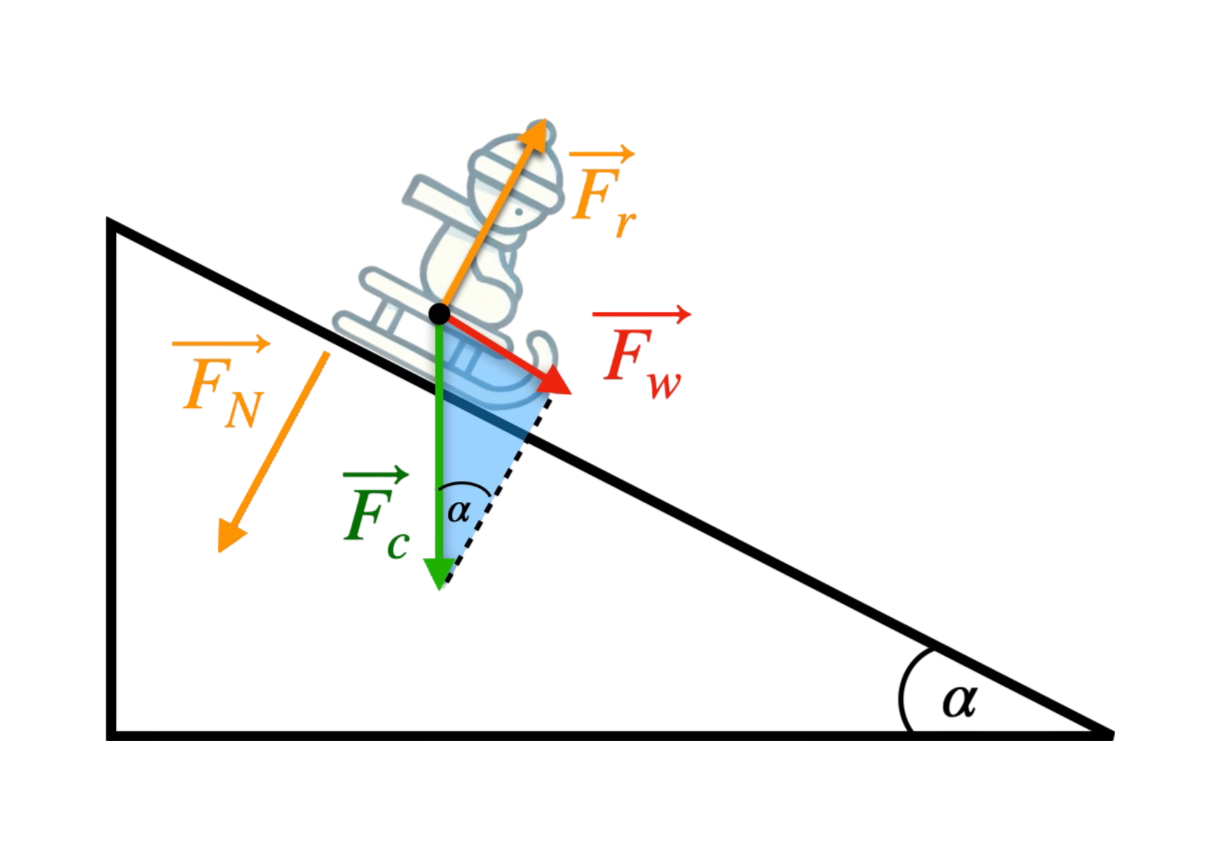
Siły działające na ciało:
Ruch ciała po równi wywołuje jedynie składowa równoległa siły \(F_W = m \cdot g sin(\alpha)\) ciężkości, co prowadzi do powstania przyspieszenia. Wartość przyspieszenia możemy wyznaczyć, korzystając z drugiej zasady dynamiki Newtona: \( F_W = m \cdot a \) Za siłe wypadkową \(F_W\) podstawiamy \(m \cdot g \cdot sin(\alpha)\): \(m \cdot g \cdot \sin(\alpha) = m \cdot a\) Skracamy \(m\) i otrzymujemy końcowy wzór: \( a = g \cdot \sin(\alpha) \) |
||
| Przyśpieszenie na Równi Pochyłej z Tarciem Podczas Zjazdu | \( a = g \cdot (\sin(\alpha) - \mu \cdot \cos(\alpha)) \) | |
Wyprowadzenie wzoru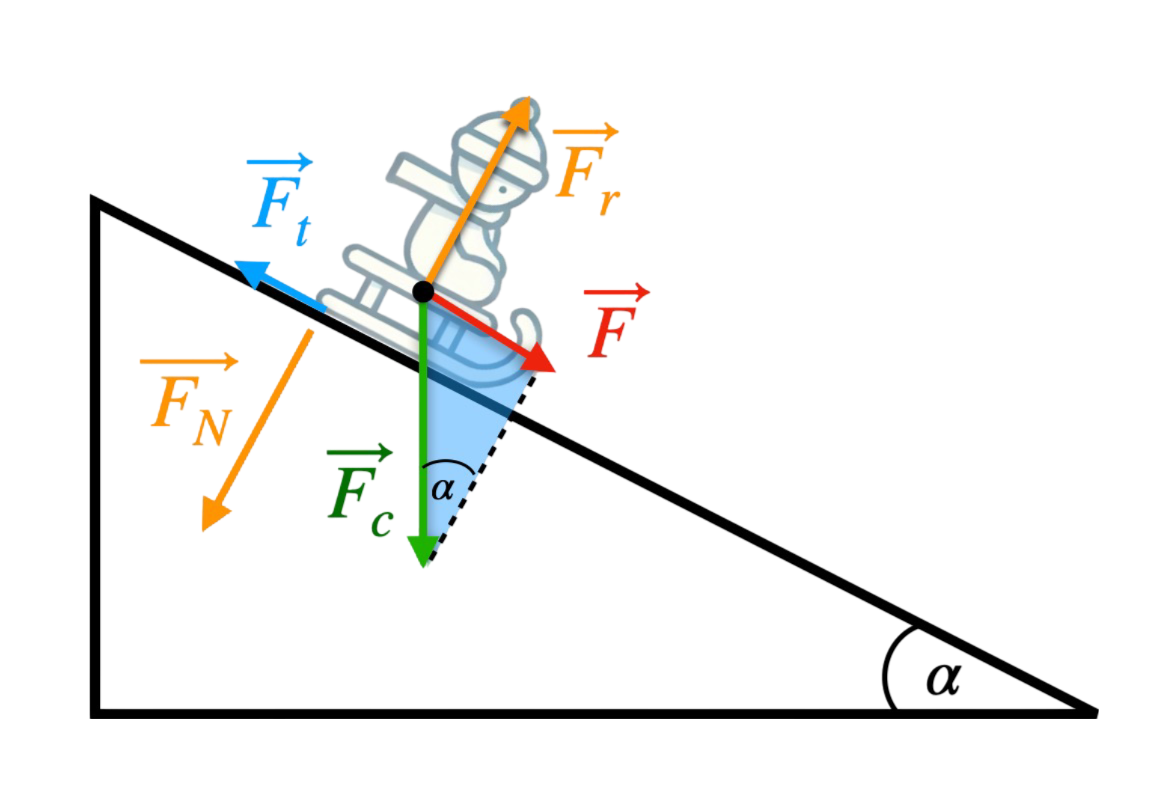
Siły działające na ciało:
Przyspieszenie ciała wynika z składowej siły ciężkości równoległej do powierzchni, pomniejszonej o siłę tarcia (zapisując rówanie sił): \( F_W = m \cdot g \cdot sin(\alpha) - F_t \) Z drugiej zasady dynamiki Newtona za \(F_W\) podstawiamy \(m \cdot a\): \( m\cdot a = m \cdot g \cdot sin(\alpha) - F_t \) Dzieląc obustronnie przez \(m\) i podstwiając, że \(F_t = m\cdot g \cdot \mu \cdot cos(alpha)\), otrzymujemy: \( a = g \cdot \sin(\alpha) - \mu \cdot g \cdot \cos(\alpha) \) |
||
| Przyśpieszenie na Równi Pochyłej z Tarciem Podczas Wjazdu | \[ a = g \cdot (\sin(\theta) + \mu_k \cdot \cos(\theta)) \] | |
Wyprowadzenie wzoru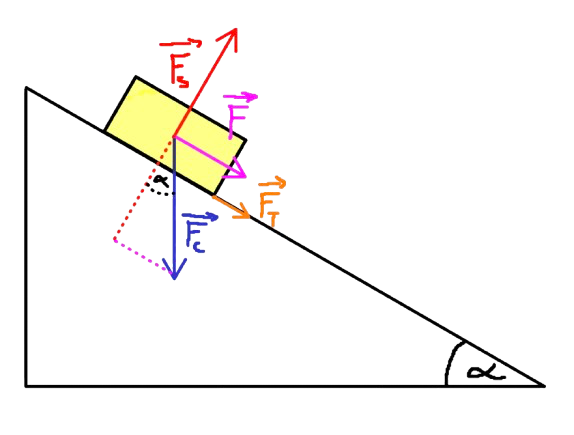
Równanie sił wzdłuż równi z uwzględnieniem tarcia kinetycznego: \[ F_w = F_{cx} + F_t \] \[ m \cdot a = mg \cdot \sin(\theta) + \mu_k \cdot mg \cdot \cos(\theta) \]Rozwiązanie względem przyspieszenia \(a\): \[ a = \frac{mg \cdot \sin(\theta) + \mu_k \cdot mg \cdot \cos(\theta)}{m} \]Uproszczenie i ostateczny wzór na przyspieszenie \(a\) z tarciem: \[ a = g \cdot (\sin(\theta) + \mu_k \cdot \cos(\theta)) \] |
||
| Prędkość Końcowa po Zjeździe z Równi Pochyłej | \(v_k = \sqrt{2 \cdot g \cdot h}\) | |
Wyprowadzenie wzoru:Ciało o masie \(m\) znajduje się na wysokości \(h\) względem dołu równi. Energia potencjalna ciała na tej wysokości to \(mgh\), gdzie: \(m\) - masa ciała \(g\) - przyspieszenie ziemskie \(h\) - wysokość Energia kinetyczna ciała to \(\frac{1}{2}mv^2\), gdzie \(v\) to prędkość ciała. Zasada zachowania energii: \(mgh = \frac{1}{2}mv^2\) Uprośćmy wzór, eliminując masę \(m\) z obu stron: \(gh = \frac{1}{2}v^2\) Pomnóżmy obustronnie przez 2: \(v^2 = 2gh\) Weź pierwiastek z obu stron: \(v = \sqrt{2gh}\) |
||
| Prędkość Końcowa po Zjeździe z Równi z Tarciem | \(v_k = \sqrt{2gh \cdot \left(1 - \frac{\mu}{\tan(\alpha)}\right)}\) | |
Wyprowadzenie wzoruCiało na początku posiada energię potencjalną związana z wysokością na równi. W miarę spadania ta energia zamienia się na energię kinetyczną. Z uwzględnieniem pracy wykonanej przez siłę tarcia, równanie tego procesu można zapisać jako: \(mgh - \frac{mv^2}{2} = W\) Gdzie:
Zakładamy, że siła tarcia \(F_{\text{tarcia}}\) wynosi \(N \cdot \mu_k\), gdzie \(N\) to nacisk na równi, a \(\mu_k\) to współczynnik tarcia kinetycznego. Nacisk \(N\) można wyrazić jako \(mg \cos(\theta)\), gdzie \(\theta\) to kąt nachylenia równi. Praca siły tarcia \(W\) wynosi \(s \cdot F_{\text{tarcia}}\), gdzie \(s\) to odległość. Podstawiając \(s = \frac{h}{\sin(\theta)}\), otrzymujemy: \(mgh - \frac{mv^2}{2} = mg \cos(\theta) \cdot \mu_k \cdot \frac{h}{\sin(\theta)}\) Uporządkowując i skracając masy, ostateczny wzór na prędkość \(v_k\) to: \(v_k = \sqrt{2gh \cdot \left(1 - \frac{\mu_k}{\tan(\theta)}\right)}\) |
||
| Maksymalna Wysokość Uzyskana Podczas Wjazdu Na Równię z Tarciem | \(h = \frac{V_0^2}{2g\left(\frac{\mu}{\tan(\theta)} + 1\right)}\) | |
Wyprowadzenie wzoru:Początkowa energia mechaniczna (\(E_{początkowa}\)): \(E_{\text{kinetyczna}} = \frac{1}{2}mv_0^2\) Energia na końcu równi (\(E_{\text{końcowa}}\)): \(E_{\text{potencjalna}} = mgh\) Praca siły tarcia (\(W_{\text{tar}}\)): \(W_{\text{tar}} = -\mu_k \cdot m \cdot g \cdot \left(\frac{h}{\sin(\alpha)}\right)\) Zasada zachowania energii: \(E_{\text{początkowa}} + W_{\text{tar}} = E_{\text{końcowa}}\) Podstawiamy wartości: \(\frac{1}{2}mv_0^2 - \left(\mu_k \cdot m \cdot g \cdot \frac{h}{\sin(\alpha)}\right) = mgh\) Skracamy masę \(m\): \(\frac{1}{2}v_0^2 - \left(\mu_k \cdot g \cdot \frac{h}{\sin(\alpha)}\right) = gh\) Przekształacamy wyrażenie i otrzymujemy: \(h = \frac{V_0^2}{2g\left(\frac{\mu}{\tan(\theta)} + 1\right)}\) |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Siła i Pęd | ||
| Siła | \(F = m \cdot a = \frac{\Delta p}{\Delta t}\) |
Legenda Wzoru:\(F\) - Siła \(m\) - Masa \(a\) - Przyspieszenie \(p\) - Pęd \(\Delta p\) - Zmiana pędu \(\Delta t\) - Zmiana czasu |
| Pęd | \(p = F \cdot t = m \cdot a \cdot t = m \cdot v\) |
Legenda Wzoru:\(p\) - Pęd \(F\) - Siła \(t\) - Czas \(m\) - Masa \(a\) - Przyspieszenie \(v\) - Prędkość |
| Zasada zachowania pędu | \(p_{c1} = p_{c2}, \quad \vec{p_1} + \vec{p_2} = \vec{p_1'} + \vec{p_2'}\) |
Legenda Wzoru:\(p_{c1}\) - Całkowity pęd układu przed zderzeniem \(p_{c2}\) - Całkowity pęd układu po zderzeniu \(\vec{p_1}\) - Pęd pierwszego ciała przed zderzeniem \(\vec{p_2}\) - Pęd drugiego ciała przed zderzeniem \(\vec{p_1'}\) - Pęd pierwszego ciała po zderzeniu \(\vec{p_2'}\) - Pęd drugiego ciała po zderzeniu \(\vec{p}\) - Wektor pędu, wskazujący kierunek i wartość pędu ciała Całkowity pęd układu przed zderzeniem (\(p_{c1}\)) jest równy całkowitemu pędowi układu po zderzeniu (\(p_{c2}\)) zgodnie z zasadą zachowania pędu. |
| Rodzaje Sił | ||
| Siła Tarcia Statycznego | \(F_{t_s} = N \cdot \mu_s\) |
Legenda Wzoru:\(F_{t_s}\) - Siła Tarcia Statycznego \(N\) - Siła Normalna \(\mu_s\) - Współczynnik Tarcia Statycznego Opis:Siła tarcia statycznego występuje, gdy przedmiot znajduje się w spoczynku i przeciwstawia się rozpoczęciu ruchu. Aby przesunąć obiekt z miejsca, siła działająca na niego musi przekroczyć siłę tarcia statycznego. |
| Siła Tarcia Kinetycznego | \(F_{t_k} = N \cdot \mu_k\) |
Legenda Wzoru:\(F_{t_k}\) - Siła Tarcia Kinetycznego \(N\) - Siła Normalna \(\mu_k\) - Współczynnik Tarcia Kinetycznego Opis:Siła tarcia kinetycznego działa, gdy przedmiot jest już w ruchu. Tarcie kinetyczne jest mniejsze od statycznego, co oznacza, że po ruszeniu przedmiotu potrzeba mniejszej siły, aby utrzymać go w ruchu. |
| Siła Dośrodkowa | \(F_d = m \cdot \frac{v^2}{r}\) |
Legenda Wzoru:\(F_d\) - Siła Dośrodkowa \(m\) - Masa ciała \(v\) - Prędkość \(r\) - Promień Krzywizny Trasy |
| Siła Ciężkości | \(F = m \cdot g\) |
Legenda Wzoru:\(F\) - Siła Ciężkości \(m\) - Masa ciała \(g\) - Przyspieszenie ziemskie (około 9.81 m/s²) |
| Równia Pochyła | ||
| Przyśpieszenie na Równi Pochyłej | \(a = g \cdot \sin(\alpha)\) |
Wyprowadzenie wzoruSiły działające na ciało:
Ruch ciała po równi wywołuje jedynie składowa równoległa siły \(F_W = m \cdot g sin(\alpha)\) ciężkości, co prowadzi do powstania przyspieszenia. Wartość przyspieszenia możemy wyznaczyć, korzystając z drugiej zasady dynamiki Newtona: \( F_W = m \cdot a \) Za siłe wypadkową \(F_W\) podstawiamy \(m \cdot g \cdot sin(\alpha)\): \(m \cdot g \cdot \sin(\alpha) = m \cdot a\) Skracamy \(m\) i otrzymujemy końcowy wzór: \( a = g \cdot \sin(\alpha) \) |
| Przyśpieszenie na Równi Pochyłej z Tarciem Podczas Zjazdu | \( a = g \cdot (\sin(\alpha) - \mu \cdot \cos(\alpha)) \) |
Wyprowadzenie wzoruSiły działające na ciało:
Przyspieszenie ciała wynika z składowej siły ciężkości równoległej do powierzchni, pomniejszonej o siłę tarcia (zapisując rówanie sił): \( F_W = m \cdot g \cdot sin(\alpha) - F_t \) Z drugiej zasady dynamiki Newtona za \(F_W\) podstawiamy \(m \cdot a\): \( m\cdot a = m \cdot g \cdot sin(\alpha) - F_t \) Dzieląc obustronnie przez \(m\) i podstwiając, że \(F_t = m\cdot g \cdot \mu \cdot cos(alpha)\), otrzymujemy: \( a = g \cdot \sin(\alpha) - \mu \cdot g \cdot \cos(\alpha) \) |
| Przyśpieszenie na Równi Pochyłej z Tarciem Podczas Wjazdu | \( a = g \cdot (\sin(\theta) + \mu_k \cdot \cos(\theta)) \) |
Wyprowadzenie wzoruRównanie sił wzdłuż równi z uwzględnieniem tarcia kinetycznego: \[ F_w = F_{cx} + F_t \] \[ m \cdot a = mg \cdot \sin(\theta) + \mu_k \cdot mg \cdot \cos(\theta) \]Rozwiązanie względem przyspieszenia \(a\): \[ a = \frac{mg \cdot \sin(\theta) + \mu_k \cdot mg \cdot \cos(\theta)}{m} \]Uproszczenie i ostateczny wzór na przyspieszenie \(a\) z tarciem: \[ a = g \cdot (\sin(\theta) + \mu_k \cdot \cos(\theta)) \] |
| Prędkość Końcowa po Zjeździe z Równi Pochyłej | \(v_k = \sqrt{2 \cdot g \cdot h}\) |
Wyprowadzenie wzoru:Ciało o masie \(m\) znajduje się na wysokości \(h\) względem dołu równi. Energia potencjalna ciała na tej wysokości to \(mgh\), gdzie: \(m\) - masa ciała \(g\) - przyspieszenie ziemskie \(h\) - wysokość Energia kinetyczna ciała to \(\frac{1}{2}mv^2\), gdzie \(v\) to prędkość ciała. Zasada zachowania energii: \(mgh = \frac{1}{2}mv^2\) Uprośćmy wzór, eliminując masę \(m\) z obu stron: \(gh = \frac{1}{2}v^2\) Pomnóżmy obustronnie przez 2: \(v^2 = 2gh\) Weź pierwiastek z obu stron: \(v = \sqrt{2gh}\) |
| Prędkość Końcowa po Zjeździe z Równi z Tarciem | \(v_k = \sqrt{2gh \cdot \left(1 - \frac{\mu}{\tan(\alpha)}\right)}\) |
Wyprowadzenie wzoruCiało na początku posiada energię potencjalną związana z wysokością na równi. W miarę spadania ta energia zamienia się na energię kinetyczną. Z uwzględnieniem pracy wykonanej przez siłę tarcia, równanie tego procesu można zapisać jako: \(mgh - \frac{mv^2}{2} = W\) Gdzie:
Zakładamy, że siła tarcia \(F_{\text{tarcia}}\) wynosi \(N \cdot \mu_k\), gdzie \(N\) to nacisk na równi, a \(\mu_k\) to współczynnik tarcia kinetycznego. Nacisk \(N\) można wyrazić jako \(mg \cos(\theta)\), gdzie \(\theta\) to kąt nachylenia równi. Praca siły tarcia \(W\) wynosi \(s \cdot F_{\text{tarcia}}\), gdzie \(s\) to odległość. Podstawiając \(s = \frac{h}{\sin(\theta)}\), otrzymujemy: \(mgh - \frac{mv^2}{2} = mg \cos(\theta) \cdot \mu_k \cdot \frac{h}{\sin(\theta)}\) Uporządkowując i skracając masy, ostateczny wzór na prędkość \(v_k\) to: \(v_k = \sqrt{2gh \cdot \left(1 - \frac{\mu_k}{\tan(\theta)}\right)}\) |
| Maksymalna Wysokość Uzyskana Podczas Wjazdu Na Równię z Tarciem | \(h = \frac{V_0^2}{2g\left(\frac{\mu}{\tan(\theta)} + 1\right)}\) |
Wyprowadzenie wzoru:Początkowa energia mechaniczna (\(E_{początkowa}\)): \(E_{\text{kinetyczna}} = \frac{1}{2}mv_0^2\) Energia na końcu równi (\(E_{\text{końcowa}}\)): \(E_{\text{potencjalna}} = mgh\) Praca siły tarcia (\(W_{\text{tar}}\)): \(W_{\text{tar}} = -\mu_k \cdot m \cdot g \cdot \left(\frac{h}{\sin(\alpha)}\right)\) Zasada zachowania energii: \(E_{\text{początkowa}} + W_{\text{tar}} = E_{\text{końcowa}}\) Podstawiamy wartości: \(\frac{1}{2}mv_0^2 - \left(\mu_k \cdot m \cdot g \cdot \frac{h}{\sin(\alpha)}\right) = mgh\) Skracamy masę \(m\): \(\frac{1}{2}v_0^2 - \left(\mu_k \cdot g \cdot \frac{h}{\sin(\alpha)}\right) = gh\) Przekształcamy wyrażenie i otrzymujemy: \(h = \frac{V_0^2}{2g\left(\frac{\mu}{\tan(\theta)} + 1\right)}\) |
Quiz - Dynamika
Dynamika
Dynamika jest dziedziną fizyki zajmującą się badaniem ruchu obiektów pod wpływem sił oraz przyczyn tego ruchu. Skupia się na związku między siłami działającymi na ciało, a jego ruchem oraz przyspieszeniem.
Podstawowymi pojęciami w dynamice są siła, masa, przyspieszenie oraz zasady dynamiki Newtona. Siła jest oddziaływaniem, które powoduje zmianę stanu ruchu ciała, a masa określa reakcję ciała na działające na nie siły.
Zasady dynamiki Newtona stanowią podstawę analizy ruchu obiektów. Pierwsza zasada mówi, że ciało pozostaje w spoczynku lub porusza się ruchem jednostajnym prostoliniowym, jeśli na nie nie działają siły zewnętrzne. Druga zasada mówi, że siła działająca na ciało jest równa iloczynowi masy ciała i jego przyspieszenia. Trzecia zasada mówi, że każde działanie ma reakcję równą, lecz przeciwną.
Dynamika umożliwia zrozumienie przyczyn ruchu obiektów oraz analizę skomplikowanych układów, w których na ciała działają różnorodne siły. Jest kluczowa w projektowaniu maszyn, pojazdów, a także w badaniach związanych z mechaniką płynów czy mechaniką kwantową.
Zastosowania dynamiki są liczne i obejmują wiele dziedzin, od inżynierii i fizyki, poprzez astronautykę, aż po medycynę i nauki biologiczne, gdzie dynamika pomaga zrozumieć ruch ciał biologicznych, takich jak ludzkie ciało czy mechanika serca.
W skrócie, dynamika jest dziedziną fizyki, która bada przyczyny ruchu ciał oraz związki między siłami a ruchem. Jest niezbędna do zrozumienia złożonych procesów ruchu w przyrodzie oraz w rozwoju nowych technologii.