Wzory pole magnetyczne
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Indukcja Magnetyczna | ||
| Wartość wektora indukcji magnetycznej | \( B = \frac{F_{\text{max}}}{I \Delta l} \) | |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( F_{\text{max}} \) - Maksymalna siła działająca na przewodnik \( I \) - Natężenie prądu \( \Delta l \) - Długość przewodnika w polu magnetycznym Opis:
Indukcja magnetyczna określa intensywność pola magnetycznego i zależy od siły działającej na przewodnik z prądem, jego długości i natężenia prądu. |
||
| Indukcja magnetyczna w odległości od przewodnika | \( B = \frac{\mu_0 I}{2 \pi r} \) | |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( \mu_0 \) - Przenikalność magnetyczna próżni \( I \) - Natężenie prądu \( r \) - Odległość od przewodnika 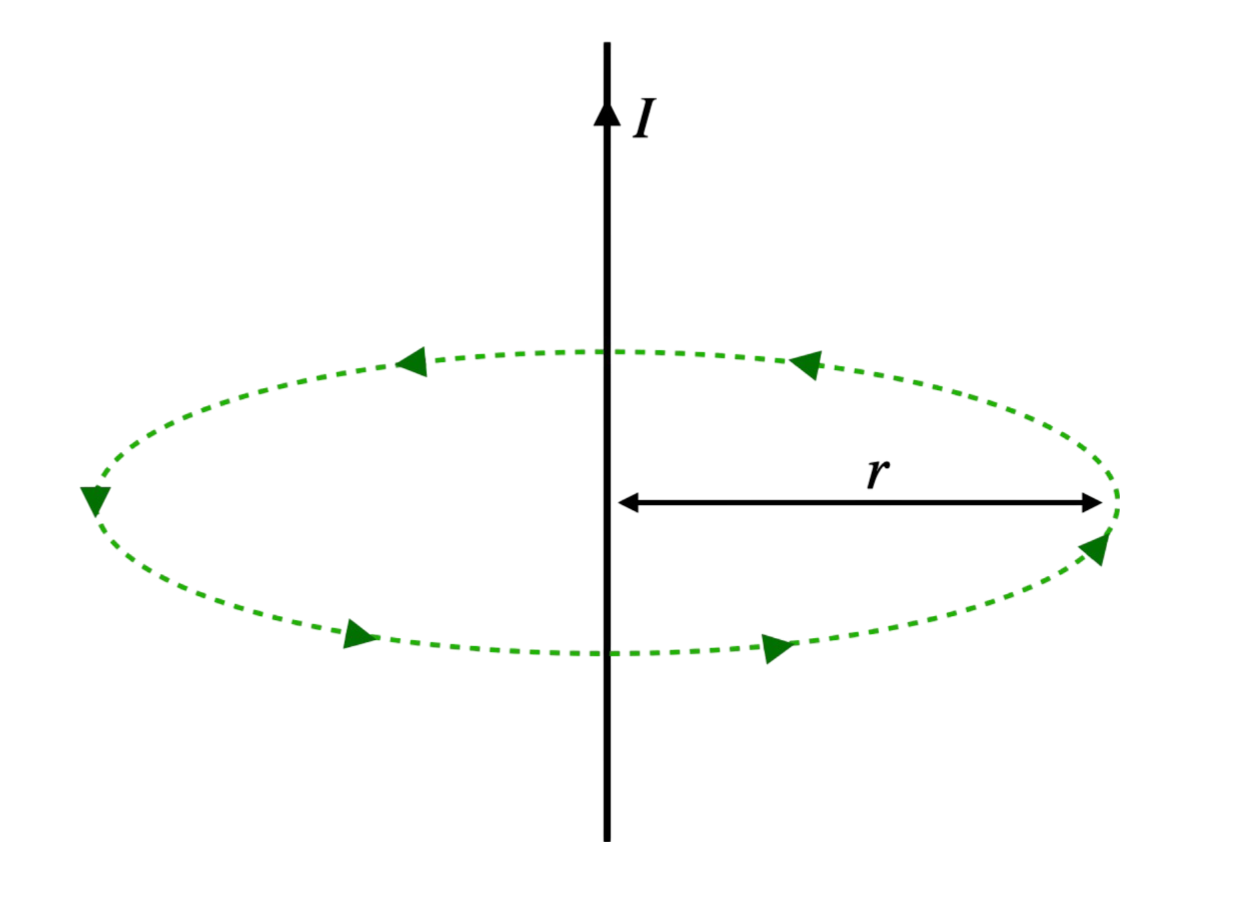
Opis:
Wzór opisuje natężenie pola magnetycznego wokół prostoliniowego przewodnika, uwzględniając natężenie prądu i odległość od przewodnika. |
||
| Indukcja we wnętrzu długiej zwojnicy | \( B = \mu_0 n \frac{I}{l} \) | |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( \mu_0 \) - Przenikalność magnetyczna próżni \( n \) - Liczba zwojów \( I \) - Natężenie prądu \( l \) - Długość zwojnicy 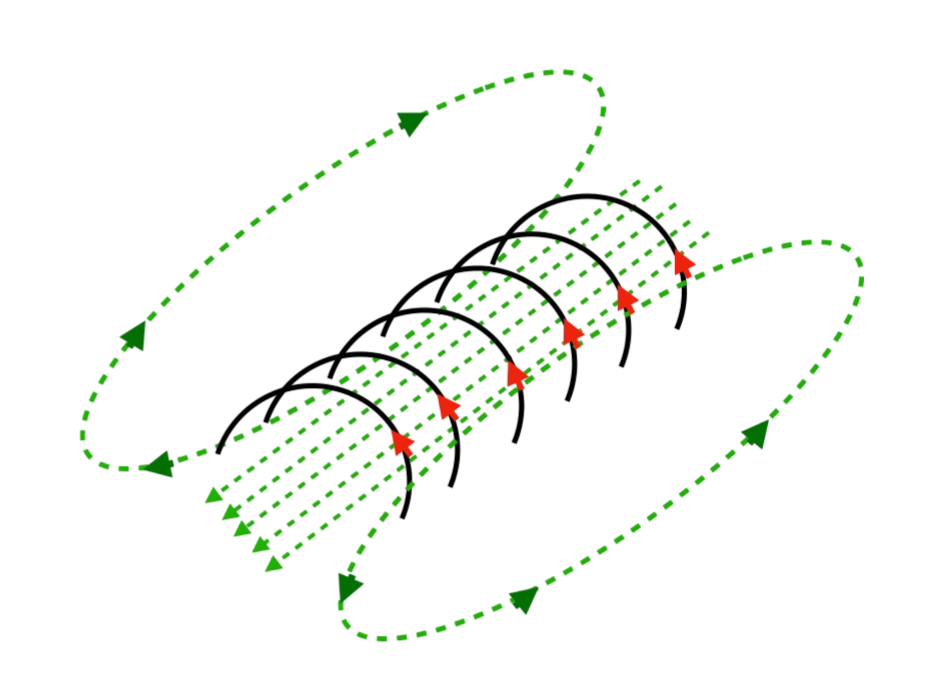
Opis:
Wzór ten opisuje indukcję magnetyczną we wnętrzu długiej zwojnicy na podstawie liczby zwojów, natężenia prądu i długości zwojnicy. |
||
| Indukcja magnetyczna dla pętli o promieniu \( r \) | \( B = \frac{\mu_0 I}{2 r} \) | |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( \mu_0 \) - Przenikalność magnetyczna próżni \( I \) - Natężenie prądu \( r \) - Promień pętli Opis:
Wzór określa natężenie pola magnetycznego w centrum pętli z prądem, uwzględniając przenikalność magnetyczną i natężenie prądu. |
||
| Siły | ||
| Siła Lorentza | \( F = q v B \sin(\theta) \) | |
Legenda Wzoru:\( F \) - Siła Lorentza \( q \) - Ładunek cząstki \( v \) - Prędkość cząstki (metry na sekundę) \( B \) - Indukcja magnetyczna \( \theta \) - Kąt między wektorem \( v \) a \( B \) 
Opis:
Siła Lorentza działa na cząstkę naładowaną poruszającą się w polu magnetycznym. Jej wartość zależy od prędkości, indukcji magnetycznej i kąta między tymi wektorami. |
||
| Siła między dwoma przewodnikami | \( F = \frac{\mu_0 I_1 I_2 \Delta l}{2 \pi r} \) | |
Legenda Wzoru:\( F \) - Siła wzajemnego oddziaływania \( \mu_0 \) - Przenikalność magnetyczna próżni \( I_1, I_2 \) - Natężenia prądów w przewodnikach \( \Delta l \) - Długość przewodników \( r \) - Odległość między przewodnikami 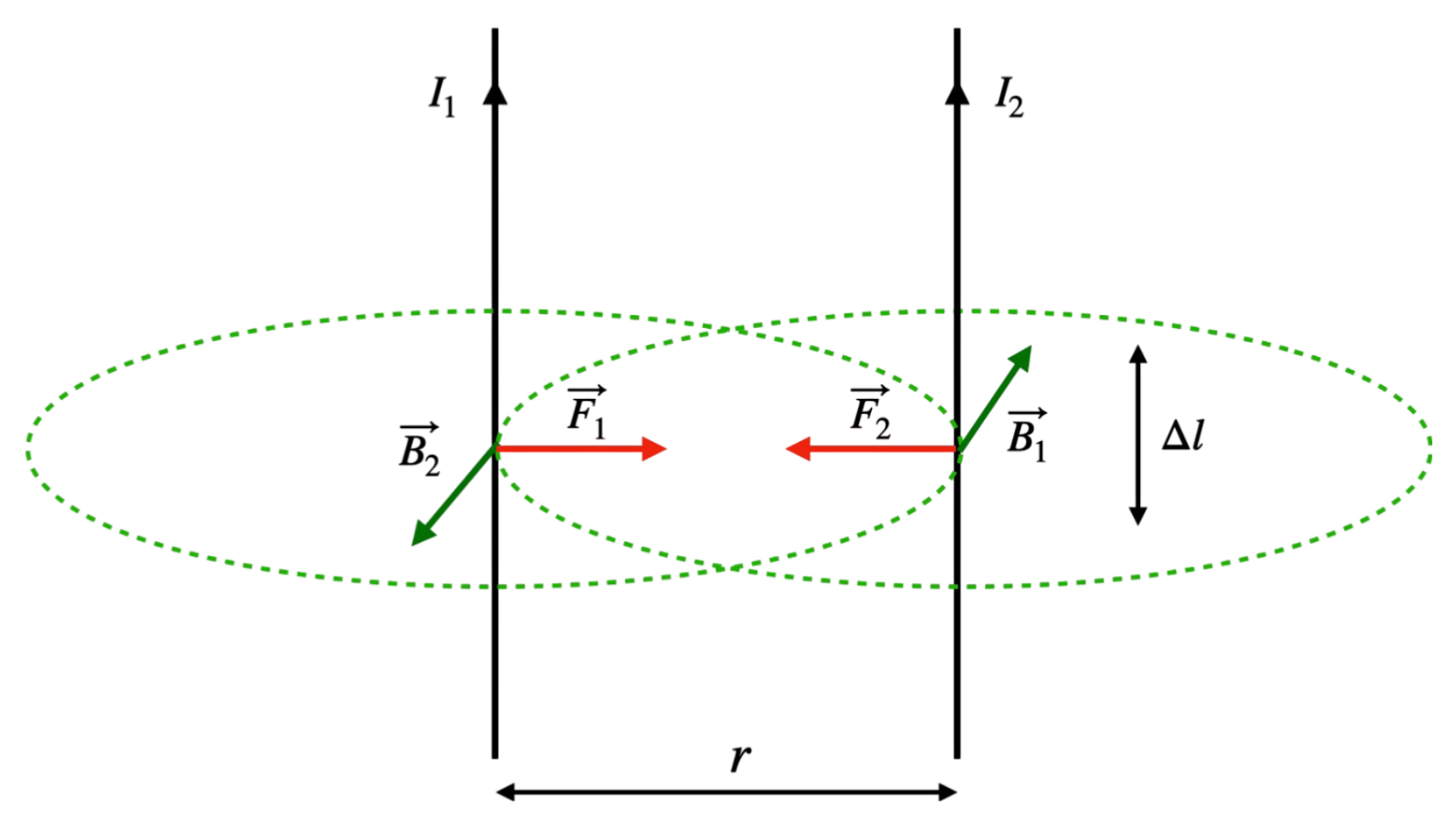
Opis:
Siła magnetyczna między dwoma równoległymi przewodnikami zależy od ich natężeń prądu, długości i odległości. |
||
| Cząstka W Polu Magnetycznym | ||
| Promień okręgu cząstki w polu magnetycznym* | \( r = \frac{m v}{q B} \) | |
Legenda Wzoru:\( r \) - Promień okręgu \( m \) - Masa cząstki \( v \) - Prędkość cząstki \( q \) - Ładunek cząstki \( B \) - Indukcja magnetyczna *zakładamy że prędkość jest prostopadła do linii pola Opis:
Promień ruchu cząstki naładowanej w polu magnetycznym zależy od jej masy, prędkości, ładunku oraz natężenia pola magnetycznego. |
||
| Okres ruchu cząstki w polu magnetycznym* | \( T = \frac{2 \pi m}{q B} \) | |
Legenda Wzoru:\( T \) - Okres ruchu \( m \) - Masa cząstki \( q \) - Ładunek cząstki \( B \) - Indukcja magnetyczna *zakładamy że prędkość jest prostopadła do linii pola Opis:
Okres ruchu cząstki w polu magnetycznym zależy od masy, ładunku cząstki oraz wartości indukcji magnetycznej. Wartość \( T \) opisuje czas potrzebny na pełen obrót cząstki po okręgu. |
||
| Reguły | ||
| Reguła lewej dłoni | ||
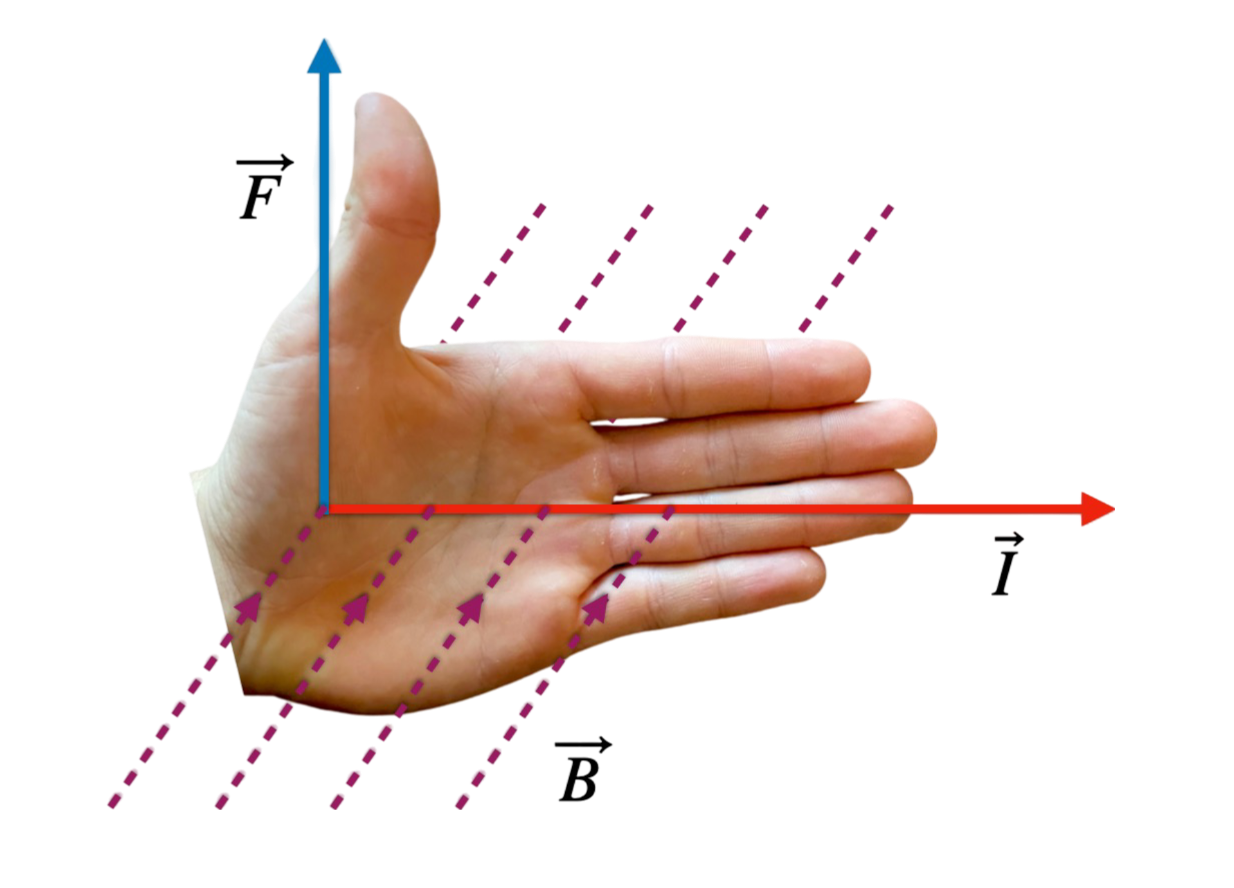
Opis:Reguła lewej dłoni określa kierunek siły działającej na przewodnik z prądem w polu magnetycznym. Palce wskazują kierunek prądu, pole magnetyczne - wnętrze dłoni, a kciuk - kierunek siły. |
||
| Reguła prawej dłoni | ||
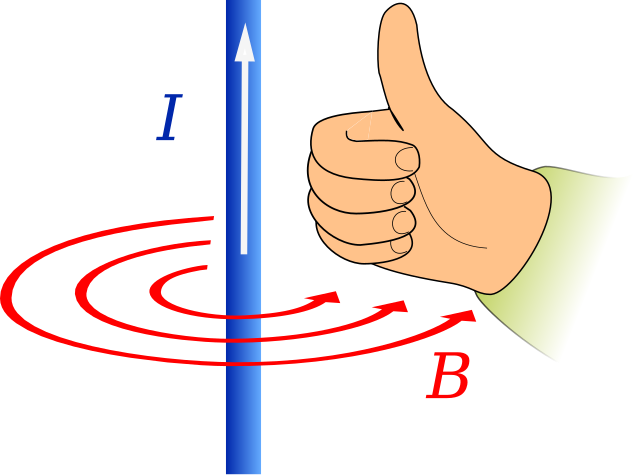
Źródło: Jfmelero Opis:Jeśli prawą dłonią obejmiemy przewodnik elektryczny tak, że kciuk wskazuje kierunek przepływu prądu elektrycznego, to zgięte palce wskażą kierunek oraz zwrot linii pola magnetycznego wokół przewodnika. |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Indukcja Magnetyczna | ||
| Wartość wektora indukcji magnetycznej | \( B = \frac{F_{\text{max}}}{I \Delta l} \) |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( F_{\text{max}} \) - Maksymalna siła działająca na przewodnik \( I \) - Natężenie prądu \( \Delta l \) - Długość przewodnika w polu magnetycznym Opis:
Indukcja magnetyczna określa intensywność pola magnetycznego i zależy od siły działającej na przewodnik z prądem, jego długości i natężenia prądu. |
| Indukcja magnetyczna w odległości od przewodnika | \( B = \frac{\mu_0 I}{2 \pi r} \) |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( \mu_0 \) - Przenikalność magnetyczna próżni \( I \) - Natężenie prądu \( r \) - Odległość od przewodnika 
Opis:
Wzór opisuje natężenie pola magnetycznego wokół prostoliniowego przewodnika, uwzględniając natężenie prądu i odległość od przewodnika. |
| Indukcja we wnętrzu długiej zwojnicy | \( B = \mu_0 n \frac{I}{l} \) |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( \mu_0 \) - Przenikalność magnetyczna próżni \( n \) - Liczba zwojów \( I \) - Natężenie prądu \( l \) - Długość zwojnicy 
Opis:
Wzór ten opisuje indukcję magnetyczną we wnętrzu długiej zwojnicy na podstawie liczby zwojów, natężenia prądu i długości zwojnicy. |
| Indukcja magnetyczna dla pętli o promieniu \( r \) | \( B = \frac{\mu_0 I}{2 r} \) |
Legenda Wzoru:\( B \) - Indukcja magnetyczna \( \mu_0 \) - Przenikalność magnetyczna próżni \( I \) - Natężenie prądu \( r \) - Promień pętli Opis:
Wzór określa natężenie pola magnetycznego w centrum pętli z prądem, uwzględniając przenikalność magnetyczną i natężenie prądu. |
| Siły | ||
| Siła Lorentza | \( F = q v B \sin(\theta) \) |
Legenda Wzoru:\( F \) - Siła Lorentza \( q \) - Ładunek cząstki \( v \) - Prędkość cząstki \( B \) - Indukcja magnetyczna \( \theta \) - Kąt między wektorem \( v \) a \( B \) 
Opis:
Siła Lorentza działa na cząstkę naładowaną poruszającą się w polu magnetycznym. Jej wartość zależy od prędkości, indukcji magnetycznej i kąta między tymi wektorami. |
| Siła między dwoma przewodnikami | \( F = \frac{\mu_0 I_1 I_2 \Delta l}{2 \pi r} \) |
Legenda Wzoru:\( F \) - Siła wzajemnego oddziaływania \( \mu_0 \) - Przenikalność magnetyczna próżni \( I_1, I_2 \) - Natężenia prądów w przewodnikach \( \Delta l \) - Długość przewodników \( r \) - Odległość między przewodnikami 
Opis:
Siła magnetyczna między dwoma równoległymi przewodnikami zależy od ich natężeń prądu, długości i odległości. |
| Cząstka w Polu Magnetycznym | ||
| Promień okręgu cząstki w polu magnetycznym | \( r = \frac{m v}{q B} \) |
Legenda Wzoru:\( r \) - Promień okręgu \( m \) - Masa cząstki \( v \) - Prędkość cząstki \( q \) - Ładunek cząstki \( B \) - Indukcja magnetyczna *zakładamy że prędkość jest prostopadła do linii pola Opis:
Promień ruchu cząstki naładowanej w polu magnetycznym zależy od jej masy, prędkości, ładunku oraz natężenia pola magnetycznego. |
| Okres ruchu cząstki w polu magnetycznym | \( T = \frac{2 \pi m}{q B} \) |
Legenda Wzoru:\( T \) - Okres ruchu \( m \) - Masa cząstki \( q \) - Ładunek cząstki \( B \) - Indukcja magnetyczna *zakładamy że prędkość jest prostopadła do linii pola Opis:
Okres ruchu cząstki w polu magnetycznym zależy od masy, ładunku cząstki oraz wartości indukcji magnetycznej. Wartość \( T \) opisuje czas potrzebny na pełen obrót cząstki po okręgu. |
| Reguły | ||
| Reguła lewej dłoni |

Opis:Reguła lewej dłoni określa kierunek siły działającej na przewodnik z prądem w polu magnetycznym. Palce wskazują kierunek prądu, pole magnetyczne - wnętrze dłoni, a kciuk - kierunek siły. |
|
| Reguła prawej dłoni |

Źródło: Jfmelero Opis:Jeśli prawą dłonią obejmiemy przewodnik elektryczny tak, że kciuk wskazuje kierunek przepływu prądu elektrycznego, to zgięte palce wskażą kierunek oraz zwrot linii pola magnetycznego wokół przewodnika. |
|
Quiz - Pole Magnetyczne
Pole Magnetyczne
Pole magnetyczne to obszar przestrzeni, w którym występują siły działające na poruszające się ładunki elektryczne oraz materiały magnetyczne, takie jak żelazo. Jest ono opisywane za pomocą wektora indukcji magnetycznej \( B \), którego jednostką jest tesla (T).
Pole magnetyczne jest generowane przez poruszające się ładunki elektryczne, takie jak prąd w przewodnikach, lub przez naturalne źródła, takie jak magnesy trwałe. Wokół przewodnika z prądem powstaje pole magnetyczne, którego kształt i intensywność zależą od wartości prądu i geometrii przewodnika.
Siły magnetyczne oddziałują na inne poruszające się ładunki elektryczne lub przewodniki z prądem. Siła Lorentza jest kluczowym pojęciem w tym zakresie, opisującym działanie pola magnetycznego na cząstki naładowane poruszające się w jego obszarze.
W zastosowaniach technicznych, pola magnetyczne są wykorzystywane w takich urządzeniach jak silniki elektryczne, generatory, transformatory i elektromagnesy. Indukcja magnetyczna umożliwia konwersję energii mechanicznej na elektryczną i odwrotnie.
Wzory opisujące pole magnetyczne, takie jak \( B = \mu_0 I / 2\pi r \) (dla przewodnika prostoliniowego) czy \( B = \mu_0 n I \) (wewnątrz zwojnicy), pozwalają precyzyjnie określić jego natężenie i kierunek. Zasady, takie jak reguła prawej dłoni, pomagają zrozumieć zależność między kierunkiem prądu, polem magnetycznym i siłą.
Pole magnetyczne odgrywa kluczową rolę w naturalnych zjawiskach, takich jak zorze polarne czy pole magnetyczne Ziemi, które chroni naszą planetę przed szkodliwym promieniowaniem kosmicznym.
Współczesne badania nad polem magnetycznym koncentrują się na jego zastosowaniach w nowoczesnych technologiach, takich jak fuzja jądrowa, diagnostyka medyczna (MRI), a także w projektowaniu wysokoefektywnych urządzeń energetycznych. Badane są również właściwości nadprzewodników, które pozwalają na tworzenie bardzo silnych pól magnetycznych bez strat energii.
Podsumowując, pole magnetyczne jest fundamentem wielu technologii i procesów fizycznych. Jego zrozumienie i wykorzystanie przyczyniło się do rozwoju takich dziedzin jak energetyka, medycyna i elektronika, czyniąc je nieodzownym elementem współczesnego świata.
