| Kategoria | Wzór | Opis Wzoru | Rodzaje Energii |
|---|---|---|
| Energia mechaniczna | \( E_m = E_k + E_p \) | |
|
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_m\) - Energia Mechaniczna \(E_k\) - Enegia Potencjalna \(E_p\) - Energia Kinetyczna |
||
| Energia kinetyczna | \(E_k = \frac{1}{2}mv^2\) | |
|
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_k\) - Energia Kinetyczna \(m\) - Masa \(v\) - Prędkość Aby wyprowadzić wzór na energię kinetyczną, zaczynając od wzoru na pracę \( W = F \cdot s \) oraz korzystając z danych zależności kinematycznych, postępujemy następująco: 1. Zależność siły od masy i przyspieszenia: \[ F = m \cdot a \] 2. Zależność przyspieszenia od prędkości początkowej i końcowej oraz czasu: \[ a = \frac{V_k - V_0}{t} \] Zakładamy, że \( V_0 = 0 \), więc: \[ a = \frac{V_k}{t} \] 3. Zależność drogi od prędkości początkowej, końcowej i czasu: \[ s = \frac{(V_k + V_0) \cdot t}{2} \] Ponownie, zakładając \( V_0 = 0 \), mamy: \[ s = \frac{V_k \cdot t}{2} \] 4. Podstawienie siły \( F \) i drogi \( s \) do wzoru na pracę \( W \): \[ W = F \cdot s \] \[ W = m \cdot a \cdot s \] 5. Podstawienie \( a \) i \( s \) z wcześniejszych wzorów: \[ W = m \cdot \left(\frac{V_k}{t}\right) \cdot \left(\frac{V_k \cdot t}{2}\right) \] 6. Uproszczenie wyrażenia: \[ W = m \cdot \frac{V_k}{t} \cdot \frac{V_k \cdot t}{2} \] \[ W = m \cdot \frac{V_k^2}{2} \] Zatem, zmiana energii to praca, dlatego praca równa się energii kinetycznej: \[ W = \Delta E_k \] Ostatecznie otrzymujemy wzór na energię kinetyczną: \[ E_k = \frac{1}{2} m V^2 \] |
||
| Energia kinetyczna ruchu obrotowego | \( E_{k_{\text{obr}}} = \frac{1}{2} I \omega^2 \) | |
|
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_{k_{\text{obr}}}\) - Energia kinetyczna ruchu obrotowego \(I\) - Moment bezwładności \( \omega \) - Prędkość kątowa |
||
| Energia potencjalna | \(E_p = mgh\) | |
|
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_p\) - Energia Potencjalna Grawitacyjna \(m\) - Masa \(g\) - Przyspieszenie Ziemskie \(h\) - Wysokość Wyprowadzenie Wzoru: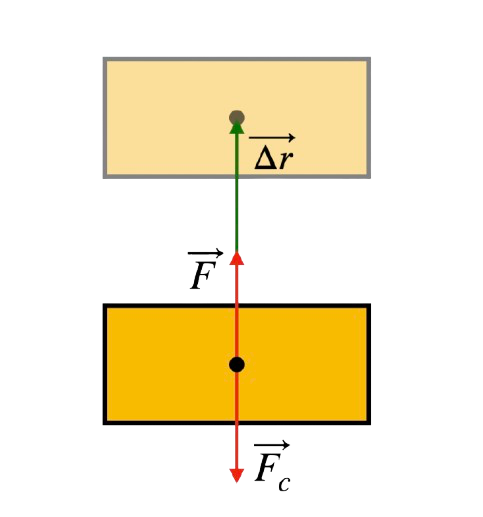
Aby wyprowadzić wzór na energię potencjalną grawitacyjną, analizujemy pracę potrzebną do podniesienia ciała na wysokość \( h \): \( W_F = F \cdot \Delta r \) Zauważamy że siła \(F\), co do wartościi jest równa \(F_c\). Z kolei \(\Delta r\) to nic innego jak nasze \(h\). Podstawiamy i otrzymujemy: \( W = F_g \cdot h = mgh \) Stąd energia potencjalna wynosi: \( E_p = mgh \) |
||
| Zasada Zachowania Energii | \(E_{m1} = E_{m2}\) | |
|
Opis Zasady Zachowania Energii: W zamkniętym układzie, całkowita energia mechaniczna \(E_m\) na początku (w momencie 1) jest równa całkowitej energii mechanicznej \(E_m\) w innym momencie (w momencie 2). Energia mechaniczna \(E_m\) jest sumą energii kinetycznej \(E_k\) i potencjalnej \(E_p\), więc mamy: \(E_{k1} + E_{p1} = E_{k2} + E_{p2}\) Legenda Wzoru:\(E_{m1}\) - Całkowita energia mechaniczna w momencie 1 \(E_{m2}\) - Całkowita energia mechaniczna w momencie 2 \(E_{k1}\) - Energia kinetyczna w momencie 1 \(E_{k2}\) - Energia kinetyczna w momencie 2 \(E_{p1}\) - Energia potencjalna w momencie 1 \(E_{p2}\) - Energia potencjalna w momencie 2 |
||
| Energia potencjalna sprężystości | \(E_p = \frac{1}{2} k x^2\) | |
|
Jednostka Energii (\(E_p\)): 1 \(J\) (dżul) Legenda Wzoru:\(E_p\) - Energia potencjalna sprężystości \(k\) - Stała sprężystości \(x\) - Odkształcenie sprężyny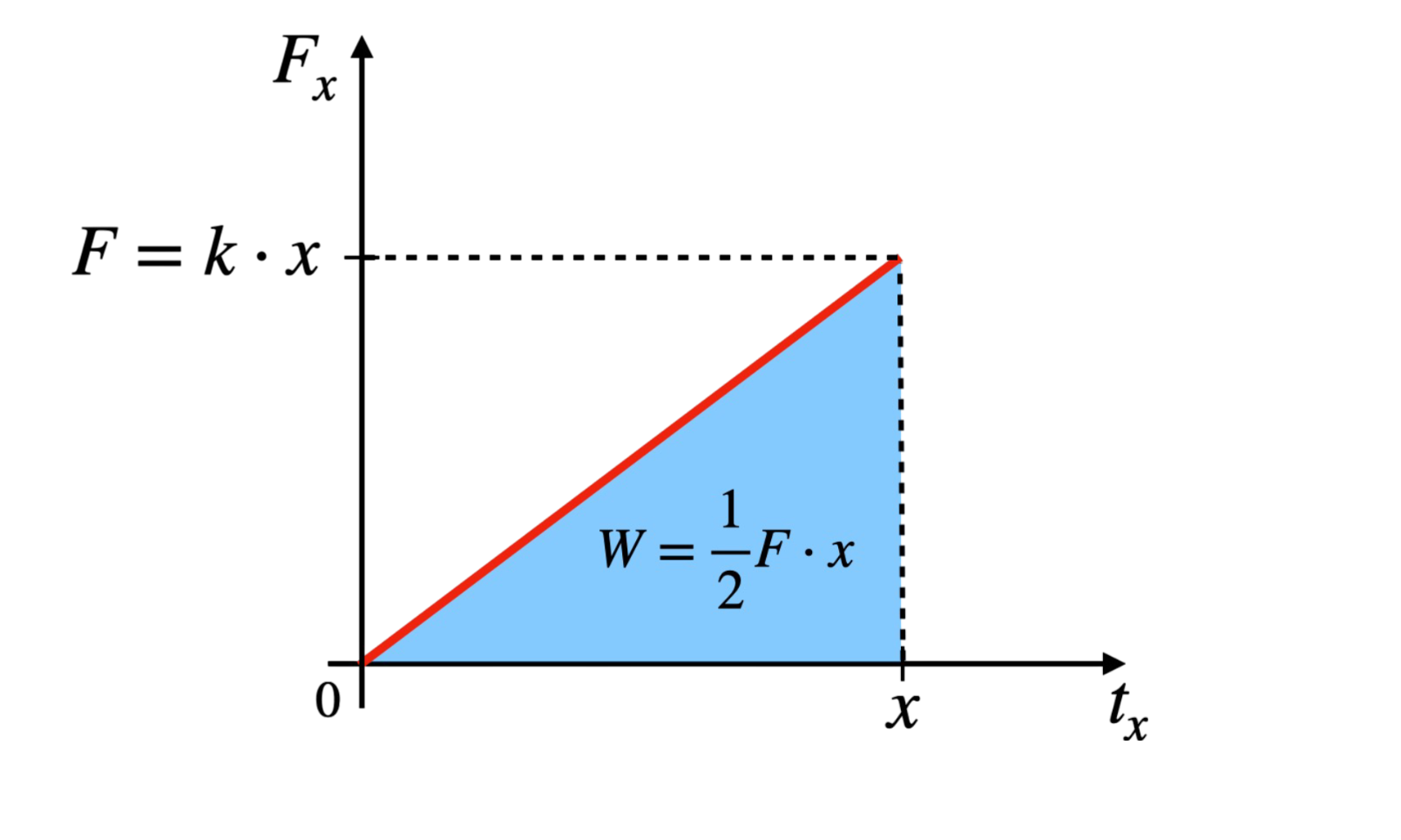 
Wyprowadzenie wzoru na energię potencjalną sprężystości opiera się na analizie pracy wykonanej podczas rozciągania sprężyny o współczynniku sprężystości \( k \) na odległość \( x \): \( W = \) Pole pod wykresem \(F(x)\) Siła \(F\) potrzebna do naciągnięcia sprężyny o długość \(x\): \( F = k\cdot x \) Stąd praca wykonana podczas rozciągania wynosi (Pole trójkąta pod wykresem): \( W = \frac{k\cdot x \cdot x}{2} \) Praca wykonana nad ciałem = Energia dostarczona ciału, więc: \( E_s = \frac{1}{2} kx^2 \) |
Praca | |
| Praca a Zmiana Energii Mechanicznej | \(W = \Delta E_m\) | |
|
Opis Wzoru: Praca \(W\) wykonana nad ciałem jest równa zmianie energii mechanicznej \( \Delta E_m \). Energia mechaniczna \(E_m\) jest sumą energii kinetycznej \(E_k\) i potencjalnej \(E_p\). Zmiana energii mechanicznej to różnica energii przed i po wykonaniu pracy: \( W = \Delta E_m = E_{m2} - E_{m1} \) Legenda Wzoru:\(W\) - Praca wykonana nad ciałem \(E_{m1}\) - Energia mechaniczna początkowa \(E_{m2}\) - Energia mechaniczna końcowa \(\Delta E_m\) - Zmiana energii mechanicznej \(E_k\) - Energia kinetyczna \(E_p\) - Energia potencjalna |
||
| Praca wykonana przez siłę | \(W = F \cdot d \cdot \cos(\alpha)\ = P \cdot t \) | |
|
Jednostka Pracy (\(W\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(W\) - Praca \(F\) - Siła \(d\) - Przesunięcie (odległość) \(\alpha\) - Kąt Między Siłą a Kierunkiem Przesunięcia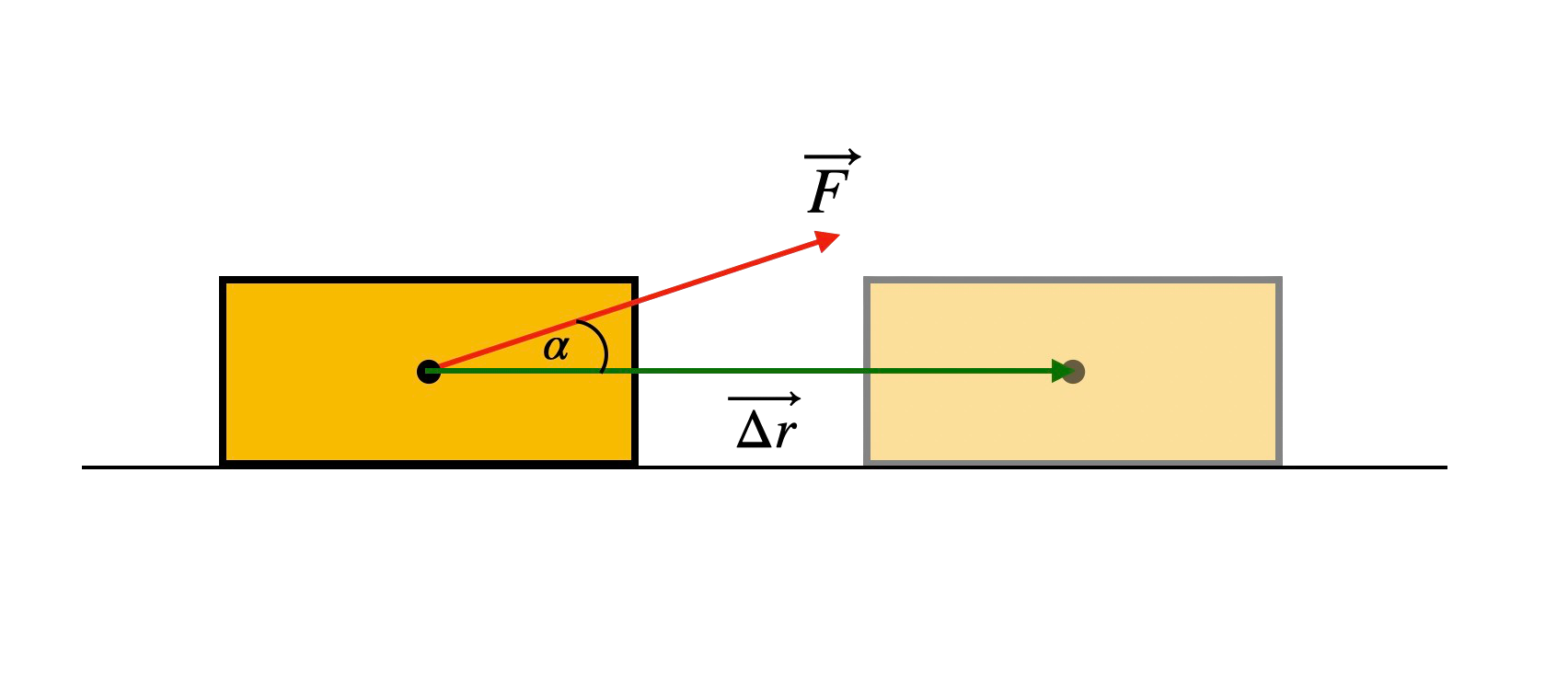 
|
||
| Moc | \( P = \frac{W}{t} = F \cdot v \) | |
|
Jednostka Mocy (\(P\)): 1 \(W\) (wat) = 1 \(\frac{J}{s}\) Legenda Wzoru:\( P \) - Moc \( W \) - Wykonana praca \( t \) - Czas \( F \) - Siła działająca \( v \) - Prędkość |
Inne | |
| Maksymalna wysokość uzyskana przez ciało (podczas rzutu pod danym kątem) | \(H = \frac{v_0^2 \cdot \sin^2(\alpha)}{2g}\) | |
|
Jednostka Wysokości (\(H\)): 1 \(m\) (metr) Legenda Wzoru:\(H\) - Wysokość Rzutu Ukośnego \(v_0\) - Początkowa Prędkość \(\alpha\) - Kąt Rzutu \(g\) - Przyspieszenie Ziemskie |
||
| Sprawność Maszyn | \(\eta = \frac{W_{\text{użyt}}}{Q_{\text{pobr}}} = \frac{Q_{\text{pobr}} - Q_{\text{odd}}}{Q_{\text{pobr}}} = \frac{T_{\text{źr}} - T_{\text{ch}}}{T_{\text{źr}}}\) | |
|
Jednostka Sprawności (\(\eta\)): Wartość bezwymiarowa (lub w procentach) Legenda Wzoru:\(\eta\) - Sprawność Maszyny \(W_{\text{użyt}}\) - Wykonana Praca Użyteczna \(Q_{\text{pobr}}\) - Ciepło Pobrane przez Maszynę \(Q_{\text{odd}}\) - Ciepło Oddane przez Maszynę \(T_{\text{źr}}\) - Temperatura Źródła Ciepła (gorącego) \(T_{\text{ch}}\) - Temperatura Odbiornika Ciepła (chłodnego) Opis Sprawności Maszyn:
Sprawność maszyny określa, jaka część energii pobranej w postaci ciepła (\(Q_{\text{pobr}}\)) jest przekształcana w użyteczną pracę \(W_{\text{użyt}}\). Można ją wyrazić jako stosunek różnicy pobranego i oddanego ciepła do pobranego ciepła: \(\eta = \frac{Q_{\text{pobr}} - Q_{\text{odd}}}{Q_{\text{pobr}}}\). W przypadku maszyn cieplnych, sprawność zależy również od temperatury źródła ciepła \(T_{\text{źr}}\) i temperatury chłodnicy \(T_{\text{ch}}\), co pozwala wyrazić sprawność jako: \(\eta = \frac{T_{\text{źr}} - T_{\text{ch}}}{T_{\text{źr}}}\). Ze względu na nieuniknione straty energii, sprawność zawsze jest mniejsza niż 1 (\(\eta < 1\)). |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Rodzaje Energii | ||
| Energia mechaniczna | \( E_m = E_k + E_p \) |
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_m\) - Energia Mechaniczna \(E_k\) - Energia Kinetyczna \(E_p\) - Energia Potencjalna |
| Energia kinetyczna | \(E_k = \frac{1}{2}mv^2\) |
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_k\) - Energia Kinetyczna \(m\) - Masa \(v\) - Prędkość Aby wyprowadzić wzór na energię kinetyczną, zaczynając od wzoru na pracę \( W = F \cdot s \) oraz korzystając z danych zależności kinematycznych, postępujemy następująco: 1. Zależność siły od masy i przyspieszenia: \[ F = m \cdot a \] 2. Zależność przyspieszenia od prędkości początkowej i końcowej oraz czasu: \[ a = \frac{V_k - V_0}{t} \] Zakładamy, że \( V_0 = 0 \), więc: \[ a = \frac{V_k}{t} \] 3. Zależność drogi od prędkości początkowej, końcowej i czasu: \[ s = \frac{(V_k + V_0) \cdot t}{2} \] Ponownie, zakładając \( V_0 = 0 \), mamy: \[ s = \frac{V_k \cdot t}{2} \] 4. Podstawienie siły \( F \) i drogi \( s \) do wzoru na pracę \( W \): \[ W = F \cdot s \] \[ W = m \cdot a \cdot s \] 5. Podstawienie \( a \) i \( s \) z wcześniejszych wzorów: \[ W = m \cdot \left(\frac{V_k}{t}\right) \cdot \left(\frac{V_k \cdot t}{2}\right) \] 6. Uproszczenie wyrażenia: \[ W = m \cdot \frac{V_k}{t} \cdot \frac{V_k \cdot t}{2} \] \[ W = m \cdot \frac{V_k^2}{2} \] Zatem, zmiana energii to praca, dlatego praca równa się energii kinetycznej: \[ W = \Delta E_k \] Ostatecznie otrzymujemy wzór na energię kinetyczną: \[ E_k = \frac{1}{2} m V^2 \] |
| Energia kinetyczna ruchu obrotowego | \( E_{k_{\text{obr}}} = \frac{1}{2} I \omega^2 \) |
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_{k_{\text{obr}}}\) - Energia kinetyczna ruchu obrotowego \(I\) - Moment bezwładności \( \omega \) - Prędkość kątowa |
| Energia potencjalna | \(E_p = mgh\) |
Jednostka Energii (\(E\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(E_p\) - Energia Potencjalna Grawitacyjna \(m\) - Masa \(g\) - Przyspieszenie Ziemskie \(h\) - Wysokość
Aby wyprowadzić wzór na energię potencjalną grawitacyjną, analizujemy pracę potrzebną do podniesienia ciała na wysokość \( h \): \( W_F = F \cdot \Delta r \) Zauważamy że siła \(F\), co do wartościi jest równa \(F_c\). Z kolei \(\Delta r\) to nic innego jak nasze \(h\). Podstawiamy i otrzymujemy: \( W = F_g \cdot h = mgh \) Stąd energia potencjalna wynosi: \( E_p = mgh \) |
| Zasada Zachowania Energii | \(E_{c1} = E_{c2}\) |
Opis Zasady: Całkowita energia mechaniczna ciała przed zdarzeniem (\(E_{c1}\)) jest równa całkowitej energii mechanicznej po zdarzeniu (\(E_{c2}\)).
Legenda Wzoru:\(E_{c1}\) - Całkowita energia mechaniczna początkowa \(E_{c2}\) - Całkowita energia mechaniczna końcowa Energia mechaniczna to suma energii kinetycznej \(E_k\) i potencjalnej \(E_p\). |
| Energia potencjalna sprężystości | \(E_p = \frac{1}{2} k x^2\) |
Jednostka Energii (\(E_p\)): 1 \(J\) (dżul) Legenda Wzoru:\(E_p\) - Energia potencjalna sprężystości \(k\) - Stała sprężystości \(x\) - Odkształcenie sprężyny |
| Praca | ||
| Praca a Zmiana Energii Mechanicznej | \(W = \Delta E_m\) |
Opis wzoru:Praca wykonana nad ciałem jest równa zmianie energii mechanicznej. Legenda Wzoru:\(W\) - Praca wykonana nad ciałem \(E_{m1}\) - Energia mechaniczna początkowa \(E_{m2}\) - Energia mechaniczna końcowa \(\Delta E_m\) - Zmiana energii mechanicznej |
| Praca wykonana przez siłę | \(W = F \cdot d \cdot \cos(\alpha)\) |
Jednostka Pracy (\(W\)): 1 \(J\) (dżul) = 1 \(N \cdot m\) Legenda Wzoru:\(W\) - Praca \(F\) - Siła \(d\) - Przesunięcie (odległość) \(\alpha\) - Kąt Między Siłą a Kierunkiem Przesunięcia
|
| Moc | \( P = \frac{W}{t} = F \cdot v \) |
Jednostka Mocy (\(P\)): 1 \(W\) (wat) = 1 \(\frac{J}{s}\) Legenda Wzoru:\( P \) - Moc \( W \) - Wykonana praca \( t \) - Czas \( F \) - Siła działająca \( v \) - Prędkość |
| Inne | ||
| Maksymalna wysokość uzyskana przez ciało (podczas rzutu pod danym kątem) | \(H = \frac{v_0^2 \cdot \sin^2(\alpha)}{2g}\) |
Jednostka Wysokości (\(H\)): 1 \(m\) (metr) Legenda Wzoru:\(H\) - Wysokość Rzutu Ukośnego \(v_0\) - Początkowa Prędkość \(\alpha\) - Kąt Rzutu \(g\) - Przyspieszenie Ziemskie |
| Sprawność Maszyn | \(\eta = \frac{W_{\text{użyt}}}{Q_{\text{pobr}}} = \frac{Q_{\text{pobr}} - Q_{\text{odd}}}{Q_{\text{pobr}}} = \frac{T_{\text{źr}} - T_{\text{ch}}}{T_{\text{źr}}}\) |
Jednostka Sprawności (\(\eta\)): Wartość bezwymiarowa (lub w procentach) Legenda Wzoru:\(\eta\) - Sprawność Maszyny \(W_{\text{użyt}}\) - Wykonana Praca Użyteczna \(Q_{\text{pobr}}\) - Ciepło Pobrane przez Maszynę \(Q_{\text{odd}}\) - Ciepło Oddane przez Maszynę \(T_{\text{źr}}\) - Temperatura Źródła Ciepła (gorącego) \(T_{\text{ch}}\) - Temperatura Odbiornika Ciepła (chłodnego) Opis Sprawności Maszyn:
Sprawność maszyny określa, jaka część energii pobranej w postaci ciepła (\(Q_{\text{pobr}}\)) jest przekształcana w użyteczną pracę \(W_{\text{użyt}}\). Można ją wyrazić jako stosunek różnicy pobranego i oddanego ciepła do pobranego ciepła: \(\eta = \frac{Q_{\text{pobr}} - Q_{\text{odd}}}{Q_{\text{pobr}}}\). W przypadku maszyn cieplnych, sprawność zależy również od temperatury źródła ciepła \(T_{\text{źr}}\) i temperatury chłodnicy \(T_{\text{ch}}\), co pozwala wyrazić sprawność jako: \(\eta = \frac{T_{\text{źr}} - T_{\text{ch}}}{T_{\text{źr}}}\). Ze względu na nieuniknione straty energii, sprawność zawsze jest mniejsza niż 1 (\(\eta < 1\)). |
Quiz - Praca, Moc, Energia
Praca, Moc, Energia
Dziedzina fizyki związana z pracą, mocą i energią bada związki między siłami, ruchem oraz przekształcaniem energii w różnych procesach. Skupia się na analizie pracy wykonanej przez siły oraz zmianie energii w układach fizycznych.
Podstawowe pojęcia w tej dziedzinie to praca, energia kinetyczna, energia potencjalna, moc oraz zasada zachowania energii. Praca jest iloczynem siły i drogi oraz opisuje efekt oddziaływania sił na obiekty. Energia kinetyczna jest związana z ruchem obiektów, a energia potencjalna z ich położeniem w polu sił. Moc to tempo przekazywania lub przekształcania energii.
Analiza pracy, mocy i energii umożliwia zrozumienie różnych procesów fizycznych, takich jak ruch obiektów, działanie maszyn, czy przekształcanie energii w silnikiach i generatory. Pozwala także na projektowanie efektywnych systemów energetycznych oraz badanie zjawisk zachodzących w przyrodzie.
Zastosowania praca, mocy i energii znajdują się w wielu dziedzinach życia, od mechaniki i budownictwa, przez inżynierię mechaniczną, aż po energię odnawialną i ochronę środowiska. Wiedza z tej dziedziny jest niezbędna również w codziennych sytuacjach, takich jak korzystanie z urządzeń elektrycznych czy poruszanie się pojazdami.
W skrócie, praca, moc i energia to kluczowe pojęcia w fizyce, które opisują związki między siłami, ruchem i przekształcaniem energii. Ich zastosowania mają szeroki zakres, od naukowych badań po praktyczne zastosowania w życiu codziennym.