Wzory kinematyka
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Ruch Prostoliniowy | ||
| Prędkość Średnia | \(v_{śr} = \frac{S_c}{t_c}\) | |
Legenda Wzoru:\(v_{śr}\) - Prędkość Średnia \(S_c\) - Całkowita Droga \(t_c\) - Całkowity Czas |
||
| Droga w Ruchu Jednostajnym | \(S = v \cdot t\) | |
Legenda Wzoru:\(S\) - Droga \(v\) - Prędkość \(t\) - Czas 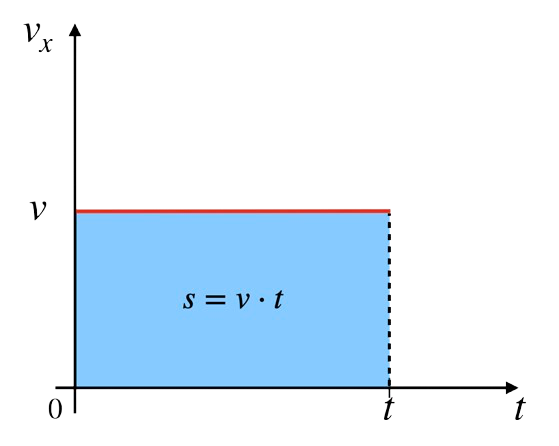
Wyprowadzenie Wzoru:Wyprowadzenie wzoru dla drogi w ruchu jednostajnym prostoliniowym polega na wykorzystaniu wykresu \(v(t)\), gdzie prędkość \(v\) jest stała. Droga \(s\) to pole prostokąta pod wykresem. |
||
| Droga w Ruchu Jednostajnie Przyspieszonym | \(S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\ = \frac{v_0 \cdot t + v_k \cdot t}{2} \) | |
Legenda Wzoru:\(S\) - Droga \(v_0\) - Początkowa Prędkość \(v_k\) - Końcowa Prędkość \(t\) - Czas \(a\) - Przyspieszenie 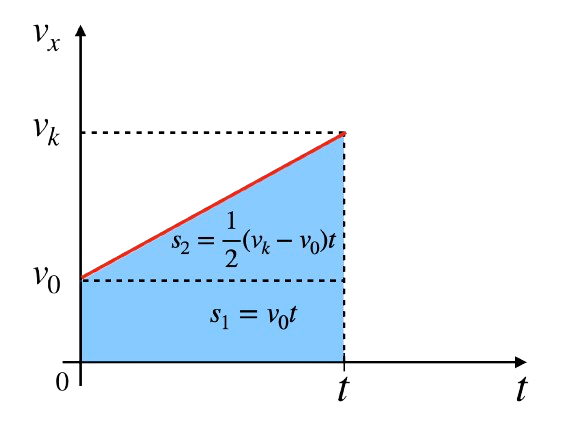
Wyprowadzenie Wzoru:Wyprowadzenie wzoru w ruchu jednostajnie przyspieszonym polega na wykorzystaniu wykresu \(v(t)\), który jest linią prostą. Droga jest równa polu trójkąta i prostokąta: \( s = s_1 + s_2 = v_0 t + \frac{1}{2}(v_k-v_0)t\) Za \(v_k-v_0\) możemy podstawić \(\Delta v \) i wykorzystać wzór na przyśpieszenie: \(a= \frac{\Delta v}{t}\), aby otrzymać ostateczny wzór: \( s =v_0 t + \frac{1}{2}at^2\) |
||
| Przyśpieszenie w Ruchu Jednostajnie Zmiennym | \(a =\frac{\Delta v}{t} =\frac{{v_k - v_0}}{{t}} = \frac{{(v_k - v_0)^2}}{{2s}} = \frac{{2s}}{{t^2}}\) | |
Legenda Wzoru:\(a\) - Przyspieszenie \(v_0\) - Prędkość Początkowa \(v_k\) - Prędkość Końcowa \(t\) - Czas \(s\) - Droga 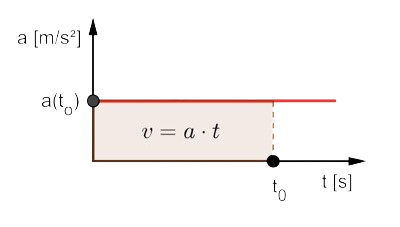
Źródło: MikeRun Wyprowadzenie:Aby uzyskać wzór na przyspieszenie (\(a\)), możemy posłużyć się ruchem jednostajnie zmiennym i podstawowymi równaniami kinematycznymi: W pierwszym przypadku wzór \(a = \frac{{v_k - v_0}}{{t}}\) wynika z definicji przyspieszenia jako zmiany prędkości w stosunku do czasu. W drugim przypadku wzór \(a = \frac{{(v_k - v_0)^2}}{{2s}}\) można uzyskać, jeśli rozważymy wzór na prędkość końcową: \(v_k = v_0 + a \cdot t\) oraz wzór na drogę \(S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\), to po przekształceniach otrzymujemy wzór na przyspieszenie (\(a\)) jako \(a = \frac{{(v_k - v_0)^2}}{{2s}}\). W trzecim przypadku wzór \(a = \frac{{2s}}{{t^2}}\) można uzyskać, wykorzystując wzór na drogę w ruchu jednostajnie zmiennym \(S = \frac{1}{2} a \cdot t^2\). Rozwiązując ten wzór względem przyspieszenia (\(a\)) otrzymujemy \(a = \frac{{2s}}{{t^2}}\), jednak jest on poprawny tylko dla ruchu, w którym prędkość początkowa lub końcowa jest równa zeru. |
||
| Czas Hamowania* | \(t_h = \frac{v}{a}\) = \(\frac{v}{gμ}\) | |
Wyprowadzenie wzoru:Zaczynamy od wzoru na przyspieszenie: \(a = \frac{\Delta V}{t}\) Chcemy uzyskać wzór na czas (\(t\)), więc przekształcamy wzór: \(t = \frac{V_0}{a}\) Podstawiamy teraz \(a = g \cdot \mu\) (przyspieszenie wynikające z oporu tarcia) i otrzymujemy: \(t = \frac{V_0}{g \cdot \mu}\) |
||
| Droga Hamowania* | \(s_h = \frac{v^2}{2a}\ = \frac{v^2}{2gμ}\) | |
Wyprowadzenie wzoru:Zaczynamy od wzoru na drogę w ruchu opóźnionym: \(s = V_0 \cdot t - \frac{1}{2} \cdot a \cdot t^2\) Podstawiamy \(a = g \cdot \mu\) oraz \(t = \frac{V_0}{g \cdot \mu}\): \(s = V_0 \cdot \frac{V_0}{g \cdot \mu} - \frac{1}{2} \cdot g \cdot \mu \cdot \left(\frac{V_0}{g \cdot \mu}\right)^2\) Uproszczając wyrażenie, otrzymujemy: \(s = \frac{V_0^2}{2 \cdot g \cdot \mu}\) |
||
| Rzuty w Polu Grawitacyjnym | ||
| Zasięg w Rzucie Poziomym | \(z = v_0 \cdot \sqrt{\frac{2h}{g}}\) | |

Wyprowadzenie wzoru:Wzór opisujący ruch pionowy to \( h = \frac{gt^2}{2} \), gdzie "h" to wysokość, "g" to przyspieszenie ziemskie, a "t" to czas. W przypadku rzutu poziomego przy braku oporów powietrza, pozioma składowa prędkości (\(V_o\)) jest stała. Zasięg (\(z\)) możemy wyznaczyć jako iloczyn \(V_o\) i czasu \(t\): \( z = V_ot \). Wyliczenie czasu: Czas ruchu \(t\) możemy uzyskać, przekształcając wzór na wysokość \(h\): \( t = \sqrt{\frac{2h}{g}} \). Znając czas, możemy obliczyć zasięg: \( z = V_ot \), gdzie \(V_o\) to pozioma prędkość początkowa. |
||
| Czas lotu ciała (podczas rzutu poziomego) | \(t = \sqrt{\frac{2H}{g}}\) | |
|
Jednostka Czasu Lotu (\(t\)): 1 \(s\) (sekunda) Legenda Wzoru:\(t\) - Czas całkowity lotu \(H\) - Wysokość początkowa rzutu \(v_0\) - Początkowa Prędkość pozioma \(g\) - Przyspieszenie Ziemskie Wyprowadzenie Wzoru:
W rzucie poziomym czas lotu zależy tylko od wysokości \(H\), z jakiej ciało zostało wyrzucone, oraz przyspieszenia ziemskiego \(g\). Czas ten można wyznaczyć z równania ruchu wzdłuż osi \(y\): \[ H = \frac{1}{2} g t^2 \] Rozwiązując względem \(t\), otrzymujemy: \[ t = \sqrt{\frac{2H}{g}} \] W przypadku rzutu poziomego, czas lotu nie zależy od prędkości poziomej \(v_0\), lecz tylko od wysokości \(H\). |
||
| Zasięg w Rzucie Ukośnym | \(z = \frac{v_0^2 \cdot \sin(2\alpha)}{g}\) | |

Wyprowadzenie wzoru:Dla rzutu ukosnego bez początkowej wysokości: Ruch poziomy opisuje równanie \(x = V_0 \cdot \cos(\alpha) \cdot t\), gdzie \(x\) to odległość, \(V_0\) to początkowa prędkość, \(\alpha\) to kąt rzutu, a \(t\) to czas lotu. Ruch pionowy opisuje równanie \(y = V_0 \cdot \sin(\alpha) \cdot t - \frac{1}{2} g t^2\), gdzie \(y\) to wysokość, \(V_0\) to początkowa prędkość, \(\alpha\) to kąt rzutu, \(g\) to przyspieszenie ziemskie, a \(t\) to czas lotu. Możemy również uzyskać wyrażenie dla zasięgu (\(z\)): \[ z = V_0 \cdot \cos(\alpha) \cdot t \]A czas lotu (\(t\)) można uzyskać z równania: \[ t = \frac{2 \cdot V_0 \cdot \sin(\alpha)}{g} \]Podstawiając to wyrażenie za czas lotu do wzoru na zasięg, otrzymujemy: \[ z = \frac{2 \cdot V_0^2 \cdot \sin(\alpha) \cdot \cos(\alpha)}{g} \]Możemy również zauważyć, że \(2 \cdot V_0^2 \cdot \sin(\alpha) \cdot \cos(\alpha)\) jest równoważne \(V_0^2 \cdot \sin(2\alpha)\). |
||
| Zasięg w Rzucie Ukośnym z Wysokością Początkową | \( z = v_0 \cdot \cos(\alpha) \left[\frac{v_0 \cdot \sin(\alpha)}{g} + \sqrt{\frac{2 \cdot \left(h_0 + v_0^2 \cdot \frac{\sin^2(\alpha)}{2g}\right)}{g}}\right] \) | |

Wyprowadzenie wzoru:Dla rzutu poziomego, gdzie opory powietrza są zaniedbywane: Czas wznoszenia (\(t_1\)) możemy obliczyć ze wzoru ruchu pionowego: \(t_1 = \frac{V \cdot \sin(\theta)}{g}\), co wynika z faktu, że czas wznoszenia to czas potrzebny na pokonanie składowej pionowej prędkości początkowej. Czas opadania (\(t_2\)) możemy obliczyć ze wzoru na czas ruchu swobodnego spadającego ciała: \(t_2 = \sqrt{\frac{2h_c}{g}}\), co wynika z faktu, że czas opadania to czas potrzebny, aby ciało wróciło na poziom terenu z pewnej wysokości maksymalnej \(h_c\). Możemy również uwzględnić, że wysokość maksymalna (\(h_c\)) jest sumą wysokości początkowej (\(h_o\)) i zmiany wysokości podczas wnoszenia (\(h_2\)), co można zapisać jako \(h_c = h_o + h_2\). Podstawiając za \(h_2\) do wzoru na \(t_2\), otrzymujemy: \(t_2 = \sqrt{\frac{2(h_o + h_2)}{g}}\). W rzucie poziomym składowa pionowa prędkości (\(V_y\)) to \(V_0 \cdot \sin(\alpha)\). Wzór na wysokość zdobytą podczas wnoszenia (\(h_2\)) dla ruchu opadającego to \(h_2 = \frac{1}{2} g t^2\), gdzie \(t\) to czas opadania. Podstawiając \(t = \frac{V_y}{g}\) (czas opadania), otrzymujemy \(h = \frac{V_0^2 \cdot \sin^2(\alpha)}{2g}\). Jeśli przyjmiemy \(h_2 = \frac{V_o^2 \cdot \sin^2(\alpha)}{2g}\), możemy podstawić to wyrażenie do wzoru na \(t_2\), co daje: \(t_2 = \sqrt{\frac{2(h_o + \frac{V_o^2 \cdot \sin^2(\alpha)}{2g})}{g}}\). Podstawiając wcześniej obliczone wartości za \(t_1\) i \(t_2\) do wzoru, otrzymujemy: \[ z = V_0 \cdot \cos(\alpha) \cdot (t_1 + t_2) \] Co można dalej rozwijać, uwzględniając wyznaczone wcześniej wartości dla \(t_1\) i \(t_2\). |
||
| Maksymalna wysokość uzyskana przez ciało | \(H = \frac{v_0^2 \cdot \sin^2(\alpha)}{2g}\) | |
|
Jednostka Wysokości (\(H\)): 1 \(m\) (metr) Legenda Wzoru:\(H\) - Wysokość Rzutu Ukośnego \(v_0\) - Początkowa Prędkość \(\alpha\) - Kąt Rzutu \(g\) - Przyspieszenie Ziemskie |
||
| Czas lotu ciała w rzucie ukośnym | \(t = \frac{2v_0 \cdot \sin(\alpha)}{g}\) | |
|
Jednostka Czasu Lotu (\(t\)): 1 \(s\) (sekunda) Legenda Wzoru:\(t\) - Czas całkowity lotu \(v_0\) - Początkowa Prędkość \(\alpha\) - Kąt Rzutu \(g\) - Przyspieszenie Ziemskie Wyprowadzenie Wzoru:
Ruch pionowy ciała podczas rzutu ukośnego opisuje równanie: \( v_y = v_0 \cdot \sin(\alpha) - g \cdot t \), gdzie \(v_y\) to prędkość pionowa. W momencie osiągnięcia maksymalnej wysokości, prędkość pionowa \(v_y = 0\). Zatem: \[ 0 = v_0 \cdot \sin(\alpha) - g \cdot \frac{t}{2} \] Przekształcając względem \(t\), otrzymujemy czas wznoszenia: \[ t_{\text{wznoszenia}} = \frac{v_0 \cdot \sin(\alpha)}{g} \] Ponieważ czas lotu obejmuje zarówno fazę wznoszenia, jak i opadania, całkowity czas lotu wynosi: \[ t = 2 \cdot t_{\text{wznoszenia}} = \frac{2v_0 \cdot \sin(\alpha)}{g} \] |
Ruch po okręgu | |
| Przyśpieszenie Dośrodkowe | \(a_d = \frac{v^2}{r}\) | |
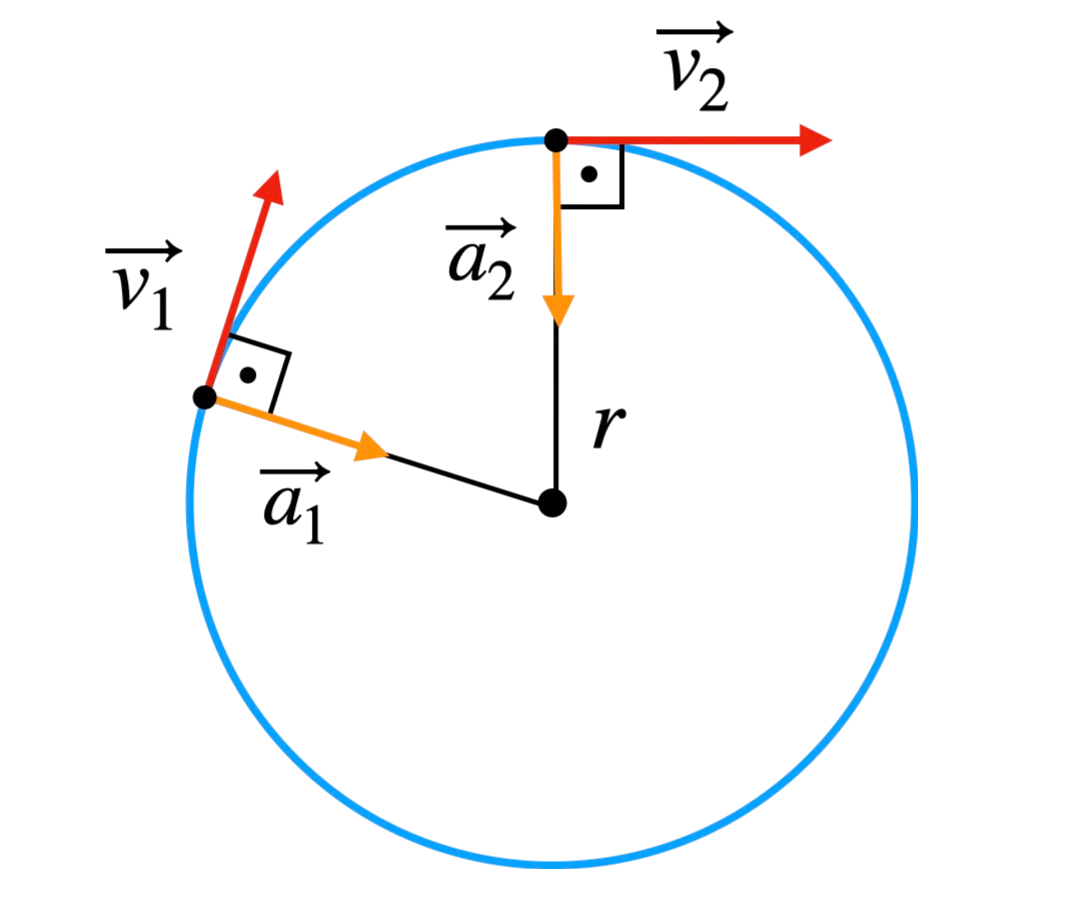
Legenda Wzoru:\(a_d\) - Przyspieszenie Dośrodkowe \(v\) - Prędkość \(r\) - Promień Krzywizny Trasy |
||
| Siła Dośrodkowa | \(F_d = m \cdot \frac{v^2}{r}\) | |
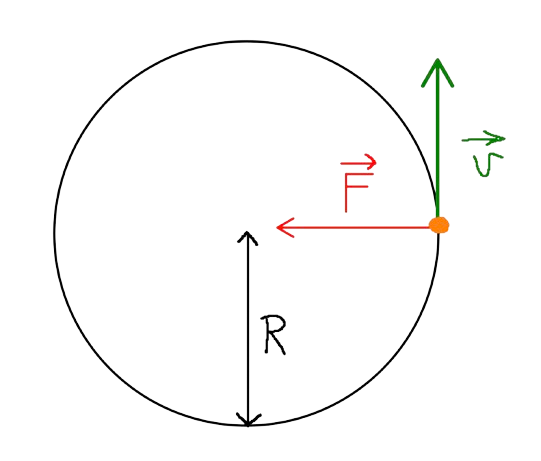
Legenda Wzoru:\(F_d\) - Siła Dośrodkowa \(m\) - Masa ciała \(v\) - Prędkość \(r\) - Promień Krzywizny Trasy |
||
| Szybkośc Kątowa | \(\omega = \frac{v}{r}\ = \frac{2\pi n}{t}\ = \frac{2\pi}{T} = 2\pi f = \frac{\Delta \alpha}{t}\) | |
Legenda Wzoru:\(\omega\) - Szybkość Kątowa \(v\) - Prędkość Liniowa \(r\) - Promień Krzywizny Trasy \(n\) - Liczba Obrotów na Sekundę \(t\) - Czas \(T\) - Okres Obrotu \(f\) - Częstotliwość Obrotowa \(\Delta \alpha\) - Kąt Obrotu |
||
| Przyśpieszenie Kątowe | \(\epsilon= \frac{a}{r}\ = \frac{\Delta \omega}{\Delta t}\) | |
Legenda Wzoru:\(\epsilon\) - Przyspieszenie Kątowe \(a\) - Przyspieszenie Liniowe \(r\) - Promień Krzywizny Trasy \(\Delta \omega\) - Zmiana Prędkości Kątowej \(\Delta t\) - Zmiana Czasu |
||
| Kategoria | Wzór | Opis Wzoru |
|---|---|---|
| Ruch Prostoliniowy | ||
| Prędkość Średnia | \(v_{śr} = \frac{S_c}{t_c}\) |
Legenda Wzoru:\(v_{śr}\) - Prędkość Średnia \(S_c\) - Całkowita Droga \(t_c\) - Całkowity Czas |
| Droga w Ruchu Jednostajnym | \(S = v \cdot t\) |
Legenda Wzoru:\(S\) - Droga \(v\) - Prędkość \(t\) - Czas 
|
| Droga w Ruchu Jednostajnie Przyspieszonym | \(S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\ = \frac{v_0 \cdot t + v_k \cdot t}{2} \) |
Legenda Wzoru:\(S\) - Droga \(v_0\) - Początkowa Prędkość \(v_k\) - Końcowa Prędkość \(t\) - Czas \(a\) - Przyspieszenie 
Wyprowadzenie Wzoru:Wyprowadzenie wzoru w ruchu jednostajnie przyspieszonym polega na wykorzystaniu wykresu \(v(t)\), który jest linią prostą. Droga jest równa polu trójkąta i prostokąta: \( s = s_1 + s_2 = v_0 t + \frac{1}{2}(v_k-v_0)t\) Za \(v_k-v_0\) możemy podstawić \(\Delta v \) i wykorzystać wzór na przyśpieszenie: \(a= \frac{\Delta v}{t}\), aby otrzymać ostateczny wzór: \( s =v_0 t + \frac{1}{2}at^2\) |
| Przyśpieszenie w Ruchu Jednostajnie Zmiennym | \(a =\frac{\Delta v}{t} =\frac{{v_k - v_0}}{{t}} = \frac{{(v_k - v_0)^2}}{{2s}} = \frac{{2s}}{{t^2}}\) |
Legenda Wzoru:\(a\) - Przyspieszenie \(v_0\) - Prędkość Początkowa \(v_k\) - Prędkość Końcowa \(t\) - Czas \(s\) - Droga 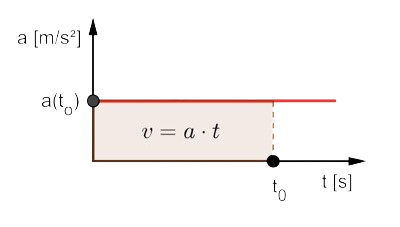
Źródło: MikeRun Wyprowadzenie:Aby uzyskać wzór na przyspieszenie (\(a\)), możemy posłużyć się ruchem jednostajnie zmiennym i podstawowymi równaniami kinematycznymi: W pierwszym przypadku wzór \(a = \frac{{v_k - v_0}}{{t}}\) wynika z definicji przyspieszenia jako zmiany prędkości w stosunku do czasu. W drugim przypadku wzór \(a = \frac{{(v_k - v_0)^2}}{{2s}}\) można uzyskać, jeśli rozważymy wzór na prędkość końcową: \(v_k = v_0 + a \cdot t\) oraz wzór na drogę \(S = v_0 \cdot t + \frac{1}{2} \cdot a \cdot t^2\), to po przekształceniach otrzymujemy wzór na przyspieszenie (\(a\)) jako \(a = \frac{{(v_k - v_0)^2}}{{2s}}\). W trzecim przypadku wzór \(a = \frac{{2s}}{{t^2}}\) można uzyskać, wykorzystując wzór na drogę w ruchu jednostajnie zmiennym \(S = \frac{1}{2} a \cdot t^2\). Rozwiązując ten wzór względem przyspieszenia (\(a\)) otrzymujemy \(a = \frac{{2s}}{{t^2}}\), jednak jest on poprawny tylko dla ruchu, w którym prędkość początkowa lub końcowa jest równa zeru. |
| Czas Hamowania* | \(t_h = \frac{v}{a}\) = \(\frac{v}{gμ}\) |
Wyprowadzenie wzoru:Zaczynamy od wzoru na przyspieszenie: \(a = \frac{\Delta V}{t}\) Chcemy uzyskać wzór na czas (\(t\)), więc przekształcamy wzór: \(t = \frac{V_0}{a}\) Podstawiamy teraz \(a = g \cdot \mu\) (przyspieszenie wynikające z oporu tarciu) i otrzymujemy: \(t = \frac{V_0}{g \cdot \mu}\) |
| Droga Hamowania* | \(s_h = \frac{v^2}{2a}\ = \frac{v^2}{2gμ}\) |
Wyprowadzenie wzoru:Zaczynamy od wzoru na drogę w ruchu opóźnionym: \(s = V_0 \cdot t - \frac{1}{2} \cdot a \cdot t^2\) Podstawiamy \(a = g \cdot \mu\) oraz \(t = \frac{V_0}{g \cdot \mu}\): \(s = V_0 \cdot \frac{V_0}{g \cdot \mu} - \frac{1}{2} \cdot g \cdot \mu \cdot \left(\frac{V_0}{g \cdot \mu}\right)^2\) Uproszczając wyrażenie, otrzymujemy: \(s = \frac{V_0^2}{2 \cdot g \cdot \mu}\) |
| Rzuty w Polu Grawitacyjnym | ||
| Zasięg w Rzucie Poziomym | \(z = v_0 \cdot \sqrt{\frac{2h}{g}}\) |

Wyprowadzenie wzoru:Wzór opisujący ruch pionowy to \( h = \frac{gt^2}{2} \), gdzie "h" to wysokość, "g" to przyspieszenie ziemskie, a "t" to czas. W przypadku rzutu poziomego przy braku oporów powietrza, pozioma składowa prędkości (\(V_o\)) jest stała. Zasięg (\(z\)) możemy wyznaczyć jako iloczyn \(V_o\) i czasu \(t\): \( z = V_ot \). Wyliczenie czasu: Czas ruchu \(t\) możemy uzyskać, przekształcając wzór na wysokość \(h\): \( t = \sqrt{\frac{2h}{g}} \). Znając czas, możemy obliczyć zasięg: \( z = V_ot \), gdzie \(V_o\) to pozioma prędkość początkowa. |
| Czas lotu ciała (podczas rzutu poziomego) | \(t = \frac{H}{v_0}\) |
Jednostka Czasu Lotu (\(t\)): 1 \(s\) (sekunda) Legenda Wzoru:\(t\) - Czas całkowity lotu \(H\) - Wysokość początkowa rzutu \(v_0\) - Początkowa Prędkość pozioma \(g\) - Przyspieszenie Ziemskie Wyprowadzenie Wzoru:
W rzucie poziomym, czas lotu zależy tylko od wysokości \(H\) z jakiej ciało zostało wyrzucone i przyspieszenia ziemskiego \(g\). Czas ten można wyznaczyć z równania ruchu wzdłuż osi \(y\): \[ H = \frac{1}{2} g t^2 \] Rozwiązując względem \(t\), otrzymujemy: \[ t = \sqrt{\frac{2H}{g}} \] W przypadku rzutu poziomego czas lotu nie zależy od prędkości poziomej \(v_0\), lecz tylko od wysokości \(H\). |
| Zasięg w Rzucie Ukośnym | \(z = \frac{v_0^2 \cdot \sin(2\alpha)}{g}\) |

Wyprowadzenie wzoru:Dla rzutu ukosnego bez początkowej wysokości: Ruch poziomy opisuje równanie \(x = V_0 \cdot \cos(\alpha) \cdot t\), gdzie \(x\) to odległość, \(V_0\) to początkowa prędkość, \(\alpha\) to kąt rzutu, a \(t\) to czas lotu. Ruch pionowy opisuje równanie \(y = V_0 \cdot \sin(\alpha) \cdot t - \frac{1}{2} g t^2\), gdzie \(y\) to wysokość, \(V_0\) to początkowa prędkość, \(\alpha\) to kąt rzutu, \(g\) to przyspieszenie ziemskie, a \(t\) to czas lotu. Możemy również uzyskać wyrażenie dla zasięgu (\(z\)): \[ z = V_0 \cdot \cos(\alpha) \cdot t \]A czas lotu (\(t\)) można uzyskać z równania: \[ t = \frac{2 \cdot V_0 \cdot \sin(\alpha)}{g} \]Podstawiając to wyrażenie za czas lotu do wzoru na zasięg, otrzymujemy: \[ z = \frac{2 \cdot V_0^2 \cdot \sin(\alpha) \cdot \cos(\alpha)}{g} \]Możemy również zauważyć, że \(2 \cdot V_0^2 \cdot \sin(\alpha) \cdot \cos(\alpha)\) jest równoważne \(V_0^2 \cdot \sin(2\alpha)\). |
| Zasięg w Rzucie Ukośnym z Wysokością Początkową | \( z = v_0 \cdot \cos(\alpha) \left[\frac{v_0 \cdot \sin(\alpha)}{g} + \sqrt{\frac{2 \cdot \left(h_0 + v_0^2 \cdot \frac{\sin^2(\alpha)}{2g}\right)}{g}}\right] \) |

Wyprowadzenie wzoru:Dla rzutu poziomego, gdzie opory powietrza są zaniedbywane: Czas wznoszenia (\(t_1\)) możemy obliczyć ze wzoru ruchu pionowego: \(t_1 = \frac{V \cdot \sin(\theta)}{g}\), co wynika z faktu, że czas wznoszenia to czas potrzebny na pokonanie składowej pionowej prędkości początkowej. Czas opadania (\(t_2\)) możemy obliczyć ze wzoru na czas ruchu swobodnego spadającego ciała: \(t_2 = \sqrt{\frac{2h_c}{g}}\), co wynika z faktu, że czas opadania to czas potrzebny, aby ciało wróciło na poziom terenu z pewnej wysokości maksymalnej \(h_c\). Możemy również uwzględnić, że wysokość maksymalna (\(h_c\)) jest sumą wysokości początkowej (\(h_o\)) i zmiany wysokości podczas wnoszenia (\(h_2\)), co można zapisać jako \(h_c = h_o + h_2\). Podstawiając za \(h_2\) do wzoru na \(t_2\), otrzymujemy: \(t_2 = \sqrt{\frac{2(h_o + h_2)}{g}}\). W rzucie poziomym składowa pionowa prędkości (\(V_y\)) to \(V_0 \cdot \sin(\alpha)\). Wzór na wysokość zdobytą podczas wnoszenia (\(h_2\)) dla ruchu opadającego to \(h_2 = \frac{1}{2} g t^2\), gdzie \(t\) to czas opadania. Podstawiając \(t = \frac{V_y}{g}\) (czas opadania), otrzymujemy \(h = \frac{V_0^2 \cdot \sin^2(\alpha)}{2g}\). Jeśli przyjmiemy \(h_2 = \frac{V_o^2 \cdot \sin^2(\alpha)}{2g}\), możemy podstawić to wyrażenie do wzoru na \(t_2\), co daje: \(t_2 = \sqrt{\frac{2(h_o + \frac{V_o^2 \cdot \sin^2(\alpha)}{2g})}{g}}\). Podstawiając wcześniej obliczone wartości za \(t_1\) i \(t_2\) do wzoru, otrzymujemy: \[ z = V_0 \cdot \cos(\alpha) \cdot (t_1 + t_2) \] Co można dalej rozwijać, uwzględniając wyznaczone wcześniej wartości dla \(t_1\) i \(t_2\). |
| Maksymalna wysokość uzyskana przez ciało | \(H = \frac{v_0^2 \cdot \sin^2(\alpha)}{2g}\) |
Jednostka Wysokości (\(H\)): 1 \(m\) (metr) Legenda Wzoru:\(H\) - Wysokość Rzutu Ukośnego \(v_0\) - Początkowa Prędkość \(\alpha\) - Kąt Rzutu \(g\) - Przyspieszenie Ziemskie |
| Czas lotu ciała w rzucie ukośnym | \(t = \frac{2v_0 \cdot \sin(\alpha)}{g}\) |
Jednostka Czasu Lotu (\(t\)): 1 \(s\) (sekunda) Legenda Wzoru:\(t\) - Czas całkowity lotu \(v_0\) - Początkowa Prędkość \(\alpha\) - Kąt Rzutu \(g\) - Przyspieszenie Ziemskie Wyprowadzenie Wzoru:
Ruch pionowy ciała podczas rzutu ukośnego opisuje równanie: \( v_y = v_0 \cdot \sin(\alpha) - g \cdot t \), gdzie \(v_y\) to prędkość pionowa. W momencie osiągnięcia maksymalnej wysokości, prędkość pionowa \(v_y = 0\). Zatem: \[ 0 = v_0 \cdot \sin(\alpha) - g \cdot \frac{t}{2} \] Przekształcając względem \(t\), otrzymujemy czas wznoszenia: \[ t_{\text{wznoszenia}} = \frac{v_0 \cdot \sin(\alpha)}{g} \] Ponieważ czas lotu obejmuje zarówno fazę wznoszenia, jak i opadania, całkowity czas lotu wynosi: \[ t = 2 \cdot t_{\text{wznoszenia}} = \frac{2v_0 \cdot \sin(\alpha)}{g} \] |
| Ruch po okręgu | ||
| Przyśpieszenie Dośrodkowe | \(a_d = \frac{v^2}{r}\) |

Legenda Wzoru:\(a_d\) - Przyspieszenie Dośrodkowe \(v\) - Prędkość \(r\) - Promień Krzywizny Trasy |
| Siła Dośrodkowa | \(F_d = m \cdot \frac{v^2}{r}\) |

Legenda Wzoru:\(F_d\) - Siła Dośrodkowa \(m\) - Masa ciała \(v\) - Prędkość \(r\) - Promień Krzywizny Trasy |
| Szybkość Kątowa | \(\omega = \frac{v}{r}\ = \frac{2\pi n}{t}\ = \frac{2\pi}{T} = 2\pi f = \frac{\Delta \alpha}{t}\) |
Legenda Wzoru:\(\omega\) - Szybkość Kątowa \(v\) - Prędkość Liniowa \(r\) - Promień Krzywizny Trasy \(n\) - Liczba Obrotów na Sekundę \(t\) - Czas \(T\) - Okres Obrotu \(f\) - Częstotliwość Obrotowa \(\Delta \alpha\) - Kąt Obrotu |
| Przyśpieszenie Kątowe | \(\epsilon= \frac{a}{r}\ = \frac{\Delta \omega}{\Delta t}\) |
Legenda Wzoru:\(\epsilon\) - Przyspieszenie Kątowe \(a\) - Przyspieszenie Liniowe \(r\) - Promień Krzywizny Trasy \(\Delta \omega\) - Zmiana Prędkości Kątowej \(\Delta t\) - Zmiana Czasu |
Quiz - Kinematyka
Kinematyka
W tej zakładzce znajdziesz wzory fizyczne, wraz z ich wyprowadzeniami. Między innymi wzór na: drogę, średnią prędkość, przyśpieszenie oraz zasięg rzutu.
Kinematyka jest dziedziną fizyki zajmującą się opisem ruchu ciał bez analizowania przyczyn tego ruchu. Skupia się głównie na badaniu drogi, prędkości i przyspieszenia ciał oraz związkach między nimi.
Podstawowymi pojęciami w kinematyce są droga, prędkość, przyspieszenie oraz czas. Droga opisuje odległość przebytą przez ciało w pewnym czasie, prędkość określa szybkość zmiany położenia, a przyspieszenie mówi nam o zmianach prędkości ciała w czasie.
Ruchy mogą być opisane zarówno w jednym, jak i w trzech wymiarach. W kinematyce jednowymiarowej, ruch odbywa się wzdłuż jednej osi, natomiast w kinematyce trójwymiarowej analizuje się ruch w trzech wymiarach przestrzennych.
Analiza kinematyczna umożliwia opisanie ruchu w sposób matematyczny za pomocą równań ruchu. Dzięki temu można prognozować przyszłe położenia ciała, określać jego prędkość w różnych momentach czasu oraz analizować różne aspekty zachowania się ciał w ruchu.
W skrócie, kinematyka jest dziedziną fizyki, która zajmuje się opisem ruchu ciał i jest kluczowa dla zrozumienia zachowania się obiektów w ruchu oraz dla rozwoju wielu dziedzin nauki i technologii.
