Wybrane wzory z fizyki

Artykuł przedstawia istotne wzory z różnych obszarów fizyki. Zawiera on kluczowe formuły dotyczące takich tematów jak gęstość, ciśnienie, energia czy moc. Dodatkowo, tekst porusza bardziej złożone zagadnienia związane z kinematyką, dynamiką, ruchem drgającym i falowym, jak również termodynamiką oraz elektrostatyką i obwodami elektrycznymi. Czytelnicy mają okazję zapoznać się z istotnymi równaniami, w tym prawami Newtona czy wzorami na prędkość i przyspieszenie. Artykuł tłumaczy także zasady dotyczące okresu i częstotliwości drgań. To znakomite źródło dla tych, którzy chcą uporządkować swoją wiedzę z fizyki i zrozumieć, jak te wzory stosowane są w praktyce.

Podstawowe wzory w fizyce

Podstawowe wzory fizyczne stanowią fundament dla zrozumienia wielu zjawisk. Zawierają istotne pojęcia i zależności niezbędne do opisów i obliczeń w różnych dziedzinach fizyki. Na przykład, prawo Newtona wyjaśnia, jak siła, masa i przyspieszenie są ze sobą powiązane, podczas gdy słynny wzór Einsteina (E=mc²) pozwala zgłębić relację między masą a energią.

Każdy wzór fizyczny jest związany z konkretnymi jednostkami, co umożliwia dokładne obliczenia:

• siłę mierzymy w niutonach (N),
• przyspieszenie w metrach na sekundę kwadratową (m/s²),
• inne jednostki również mają swoje zastosowanie.

Tabela z wzorami fizycznymi ilustruje te powiązania i jednostki, co ułatwia zarówno naukę, jak i praktyczne zastosowanie wiedzy. Opanowanie tych wzorów jest kluczowe dla studentów oraz profesjonalistów zajmujących się fizyką i pokrewnymi dziedzinami.

Dzięki tym wzorom możliwe jest rozwiązywanie problemów teoretycznych i praktycznych w takich obszarach jak inżynieria, medycyna czy technologia. Wiedza o podstawowych wzorach fizycznych jest zatem nieoceniona zarówno w nauce, jak i w życiu codziennym.

gęstość i ciśnienie

Gęstość, oznaczana symbolem rho, to istotne pojęcie w fizyce. Jest to stosunek masy do objętości, co przedstawia wzór rho = m/V. Jednostką miary jest kilogram na metr sześcienny (kg/m³). Wiedza na temat gęstości materiałów pozwala lepiej zrozumieć ich właściwości i zastosowania w różnych dziedzinach, takich jak inżynieria i technologia.

Ciśnienie, oznaczane literą p, opisuje siłę działającą na jednostkę powierzchni, co wyraża się wzorem p = F/s i mierzy w paskalach (Pa). W kontekście hydrostatyki, ciśnienie hydrostatyczne uwzględnia gęstość cieczy, przyspieszenie ziemskie oraz wysokość słupa cieczy, zgodnie z równaniem p = rho * g * h. Zrozumienie tych zależności jest niezbędne przy analizie cieczy i gazów.

energia i moc

Energia i moc to kluczowe pojęcia w fizyce, które odgrywają istotną rolę w analizie systemów. Energia kinetyczna (E_k) obliczana jest poprzez wzór: E_k = mV²/2, gdzie masa (m) oraz prędkość (V) mają fundamentalne znaczenie. Natomiast energia potencjalna grawitacyjna jest wyrażana wzorem ΔE_p = m * g * h, a jej wartość zależy od masy, przyspieszenia ziemskiego (g) oraz wysokości (h). Moc (P) definiuje się jako praca (W) wykonana w określonym czasie (t), co ilustruje równanie P = W/t. Te podstawowe formuły są niezbędne do zrozumienia wpływu energii i mocy na różne systemy fizyczne. Poznanie tych relacji jest kluczowe przy analizie zjawisk związanych z energią i mechaniką.

Wzory z zakresu kinematyki

Kinematyka to gałąź fizyki skupiająca się na opisie ruchu ciał bez analizy jego przyczyn. Istotne wzory kinematyczne dotyczą takich wielkości jak prędkość, przyspieszenie, droga oraz czas. Prędkość (v) można wyrazić równaniem v = Δr/Δt, gdzie Δr oznacza zmianę położenia, a Δt to czas. Przyspieszenie (a) opisuje wzór a = Δv/Δt, gdzie Δv to zmiana prędkości.

W przypadku ruchu jednostajnego po okręgu, prędkość kątowa (ω) jest obliczana jako ω = Δα/Δt. Relacja między prędkością kątową a liniową jest wyrażona równaniem v = ωr, gdzie r to promień okręgu. Dla ruchu prostoliniowego jednostajnie zmiennego prędkość można wyznaczyć za pomocą wzoru v = v₀ + at, a drogę poprzez s = v₀t + 1/2 at², gdzie v₀ jest prędkością początkową, a s – przebyta droga.

Przyspieszenie dośrodkowe (ad) w ruchu po okręgu określa się jako ad = v²/r = vω = ω²r. Natomiast w ruchu zmiennym przyspieszenie kątowe (ε) wyraża się wzorem ε = Δω/Δt. Te równania są kluczowe dla zrozumienia dynamiki ruchu i mają rozległe zastosowanie w analizie problemów fizycznych.

prędkość i przyspieszenie

Prędkość (V) odnosi się do dystansu pokonywanego w danym czasie, co wyrażamy wzorem V = s/t. Przyspieszenie (a) opisuje zmianę prędkości w czasie i można je określić jako a = ΔV/t. Podczas gdy prędkość informuje, jak szybko porusza się dany obiekt, przyspieszenie wskazuje, w jaki sposób ta prędkość ulega zmianie.

W przypadku ruchu jednostajnego prostoliniowego prędkość pozostaje niezmienna, a przyspieszenie wynosi zero. Natomiast przyspieszenie kątowe odnosi się do ruchu po okręgu i oblicza się je przy pomocy wzoru: ε = Δω/Δt, gdzie ω oznacza prędkość kątową. Te wzory są niezbędne do analizy ruchu oraz dynamiki obiektów.

droga i czas

Droga i czas odgrywają istotną rolę w analizie ruchu w fizyce. Przy ruchu jednostajnie przyspieszonym, długość trasy (s) wyliczamy ze wzoru: s = at²/2, gdzie a to przyspieszenie, a t to czas. Czas jest kluczowym parametrem, dzięki któremu można dokładnie przeprowadzać obliczenia dynamiczne. Zrozumienie tych relacji umożliwia precyzyjne modelowanie oraz przewidywanie zachowań obiektów będących w ruchu.

Wzory z zakresu dynamiki

Dynamika to dziedzina fizyki zajmująca się badaniem ruchu ciał, uwzględniając działające na nie siły. Kluczowe wzory w tej dziedzinie odnoszą się do takich pojęć jak siła ciężkości oraz zasady dynamiki Newtona. Siłę ciężkości (F_g) można obliczyć poprzez pomnożenie masy (m) przez przyspieszenie ziemskie (g): F_g = m * g, a jednostką tej siły jest niuton (N).

Zgodnie z drugą zasadą dynamiki Newtona, przyspieszenie ciała (a) jest wprost proporcjonalne do siły (F) działającej na to ciało i odwrotnie proporcjonalne do jego masy, co wyraża wzór: F = m * a. To prawo pozwala lepiej zrozumieć, jak siła wpływa na zmianę prędkości ciała.

Dodatkowo, moment siły (M) jest iloczynem siły (F) i ramienia siły (r), zgodnie z równaniem M = r * F * sin ∢(r, F). Moment bezwładności (I) z kolei to suma iloczynów masy i kwadratu odległości od osi obrotu, co opisuje wzór I = ∑ mi * ri². To pojęcie jest kluczowe dla zrozumienia ruchu obrotowego.

Energia kinetyczna ruchu postępowego (E_kin) wyrażana jest jako połowa iloczynu masy i kwadratu prędkości: E_kin = 1/2 * m * v². W przypadku ruchu obrotowego, energia kinetyczna to połowa momentu bezwładności i kwadratu prędkości kątowej, co przedstawia wzór E_kin = 1/2 * I * ω². Te wzory są niezbędne do analizowania sił i ruchu w różnych systemach fizycznych.

siła ciężkości i siła wyporu

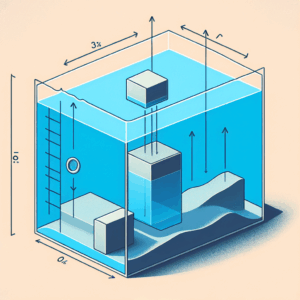
Siła ciężkości oraz wyporu to kluczowe pojęcia w dziedzinie dynamiki. Siłę ciężkości (F) można wyrazić wzorem F = m * g, gdzie m to masa, a g oznacza przyspieszenie ziemskie wynoszące 9.81 m/s². Oddziałuje ona na każde ciało znajdujące się w pobliżu powierzchni Ziemi, przyciągając je w stronę jej środka.

Z kolei siła wyporu (F_w) jest obliczana jako F_w = rho * g * V. W tym przypadku rho reprezentuje gęstość cieczy, a V to objętość zanurzonego obiektu. Zgodnie z zasadą Archimedesa, siła wyporu jest równa ciężarowi cieczy, którą ciało wypiera. Działa przeciwnie do siły ciężkości, co decyduje o tym, czy obiekty unoszą się, czy też toną w cieczy, w zależności od ich gęstości. Zrozumienie tych sił jest kluczowe przy analizie zjawisk dotyczących pływalności oraz równowagi ciał w płynach.

druga zasada dynamiki Newtona

Druga zasada dynamiki Newtona stanowi fundamentalny wzór w fizyce, opisując relację między siłą, masą a przyspieszeniem obiektu. Wyrażenie to przybiera postać: F = m * a, gdzie:

• F oznacza siłę mierzoną w niutonach (N),
• m odnosi się do masy wyrażanej w kilogramach (kg),
• a symbolizuje przyspieszenie w metrach na sekundę do kwadratu (m/s²).

Zastosowanie tej zasady pozwala określić tempo przyspieszenia ciała, kiedy znamy jego masę oraz działającą na nie siłę. Zrozumienie tego prawa jest niezbędne do analizy ruchu i przewidywania zachowania obiektów pod wpływem różnorodnych sił.

Wzory z zakresu ruchu drgającego i falowego

Drgania i zjawiska falowe odgrywają kluczową rolę w fizyce, obejmując oscylacje oraz propagację fal. Warto zaznajomić się z kilkoma istotnymi wzorami dotyczącymi tego zagadnienia.

• okres drgań (T) oraz częstotliwość (f) są ze sobą nierozerwalnie związane,
• ich wzajemna odwrotność przedstawiona jest wzorem: T = 1/f,
• częstotliwość, wyrażana w hercach (Hz), wskazuje liczbę drgań odbywających się w ciągu sekundy.

Prędkość fali (v) oblicza się, mnożąc długość fali (λ) przez częstotliwość: v = λ * f. Długość fali oznacza odległość między kolejnymi grzbietami lub dolinami, mierzona w metrach. Prędkość fali określa szybkość, z jaką fala przemieszcza się przez dane środowisko.

Drgania i fale mechaniczne występują w wielu dziedzinach, takich jak inżynieria czy medycyna. Z tego powodu znajomość wspomnianych wzorów jest istotna dla studentów oraz specjalistów związanych z fizyką i pokrewnymi obszarami.

okres i częstotliwość drgań

Okres drgań (T) to czas potrzebny na wykonanie jednego pełnego cyklu drgającego. Oblicza się go za pomocą wzoru T = t/n, gdzie t oznacza całkowity czas drgań, a n to ilość cykli. Wynik podawany jest w sekundach.

Częstotliwość (f) z kolei określa, ile cykli zachodzi w jednostce czasu i jest odwrotnością okresu, co wyraża się wzorem f = 1/T. Mierzona jest w hercach (Hz), co wskazuje na liczbę drgań w ciągu sekundy.

Te pojęcia są niezwykle ważne przy analizie ruchu oscylacyjnego. Pozwalają zrozumieć prędkość oscylacji w danym układzie. Wiedza na temat okresu i częstotliwości drgań jest kluczowa w wielu dziedzinach, takich jak:

• akustyka,
• inżynieria budowlana,
• medycyna.

prędkość i długość fali

Prędkość fali (v) wskazuje, jak szybko fala przemieszcza się w określonym środowisku. Aby ją obliczyć, wystarczy pomnożyć długość fali (λ) przez częstotliwość (f), co przedstawia wzór: v = λ * f. Długość fali, podawana w metrach, to dystans między kolejnymi szczytami lub dolinami. Znajomość tych parametrów jest istotna w wielu dziedzinach, takich jak akustyka czy telekomunikacja. Zrozumienie, jak fale się rozchodzą, pozwala na projektowanie skutecznych systemów transmisji.

Wzory z zakresu termodynamiki

W termodynamice fundamentalną rolę odgrywa pierwsza zasada, odnosząca się do zachowania energii. Jest ona wyrażona równaniem: ΔU = Q – W. W tym wzorze ΔU oznacza zmianę energii wewnętrznej systemu, Q to ciepło dodane do tego systemu, a W to praca wykonana przez system. Dzięki tej zasadzie możemy lepiej zrozumieć, jak ciepło i praca oddziałują na kondycję systemu.

Innym istotnym elementem jest przeliczanie temperatur. Temperaturę w stopniach Celsjusza można przekształcić na kelwiny, korzystając ze wzoru: T(K) = T(°C) + 273.15. To zrozumienie jest niezbędne przy analizie procesów, takich jak zmiany fazowe czy reakcje chemiczne.

W termodynamice stosuje się także inne wzory, wspomagające analizę, jak choćby równanie stanu gazu doskonałego, które łączy ciśnienie, objętość i temperaturę. Te zasady są kluczowe w naukach ścisłych i technice, umożliwiając precyzyjne modelowanie zachowania systemów termodynamicznych.

pierwsza zasada termodynamiki

Pierwsza zasada termodynamiki stanowi fundamentalne prawo dotyczące zachowania energii w zamkniętym układzie. Wyraża ją równanie: ΔE_w = W + Q. W tym zapisie:

• ΔE_w oznacza zmianę energii wewnętrznej,
• W to praca wykonana na systemie,
• Q to ciepło dostarczone do niego.

Zasada ta ilustruje, że energia nie znika, a jedynie przekształca się w różne formy. Dzięki niej można lepiej zrozumieć, jak energia przepływa i ulega transformacjom w systemach fizycznych. Odgrywa ona istotną rolę w analizach termodynamicznych, zarówno w naukach ścisłych, jak i w inżynierii.

temperatura i jej przeliczanie

Temperatura odgrywa kluczową rolę w termodynamice, a przeliczanie jej między różnymi skalami jest niezbędne w nauce i technice. Na przykład, aby zamienić stopnie Fahrenheita (T_f) na Celsjusza (T_c), stosujemy wzór: T_c = 5/9 (T_f – 32).

Skala Celsjusza jest szeroko używana w wielu krajach, co sprawia, że konwersja do Fahrenheita nabiera znaczenia w międzynarodowych projektach badawczych oraz przemysłowych. Takie wzory fizyczne, jak ten przedstawiony, umożliwiają precyzyjne obliczenia i stanowią fundament nauk ścisłych. Umiejętność przeliczania temperatury jest kluczowa dla analizy procesów termodynamicznych i projektowania systemów pracujących w różnych warunkach temperaturowych.

Wzory z zakresu elektrostatyki i prądu elektrycznego

Wzory z zakresu elektrostatyki oraz prądu elektrycznego odgrywają istotną rolę w zgłębianiu zjawisk związanych z ładunkami i przepływem prądu. Elektrostatyka koncentruje się na oddziaływaniach ładunków w stanie spoczynku, natomiast prąd elektryczny dotyczy ich ruchu w obwodach. Kluczowe pojęcia to natężenie prądu, napięcie, prawo Ohma oraz praca prądu.

Natężenie prądu, oznaczane jako I, wyrażamy w amperach (A). Oznacza ono ilość ładunku przechodzącego przez przekrój przewodnika w określonym czasie. Wzór na to zjawisko to I = Q/t, gdzie Q jest ładunkiem w kulombach (C), a t czasem w sekundach (s). Z kolei napięcie, symbolizowane jako U, mierzymy w woltach (V) i stanowi różnicę potencjałów między dwoma punktami obwodu. Można je obliczyć używając prawa Ohma: U = I * R, gdzie R to opór elektryczny mierzony w omach (Ω).

Prawo Ohma jest fundamentalne i opisuje relacje pomiędzy napięciem, natężeniem oraz oporem w obwodzie. Umożliwia ono wyznaczenie jednej z tych wartości, gdy znane są pozostałe dwie. Praca prądu, oznaczana jako W, to iloczyn napięcia, natężenia i czasu, czyli W = U * I * t. Jednostką pracy jest dżul (J), co pozwala ocenić zużycie energii przez obwód w określonym czasie.

Znajomość tych wzorów jest kluczowa dla analizy i projektowania systemów elektrycznych, a także w rozwiązywaniu problemów związanych z przepływem prądu w różnorodnych zastosowaniach technologicznych.

natężenie i napięcie prądu

Natężenie prądu (I) oraz napięcie (U) należą do fundamentalnych pojęć w dziedzinie fizyki elektrycznej. Natężenie określa ilość ładunku (q) przepływającego przez przewodnik w określonym czasie (t), co opisuje wzór I = q/t. Jednostką miary natężenia jest amper (A). Z kolei napięcie to praca wykonana na jednostkę ładunku, przedstawiana równaniem U = W/q, gdzie W symbolizuje pracę. Mierzymy je w woltach (V). Zrozumienie tych zasadniczych zależności jest istotne przy analizie i projektowaniu układów elektrycznych.

prawo Ohma i praca prądu

Prawo Ohma oraz praca prądu to kluczowe zagadnienia w elektrostatyce i elektryczności. Prawo Ohma opisuje, jak napięcie (U), natężenie (I) i opór (R) są ze sobą powiązane w obwodzie elektrycznym. Wyrażamy to równaniem U = R * I. Dzięki temu możemy obliczyć jedną z tych wielkości, znając dwie pozostałe.

Praca prądu (W) natomiast dotyczy energii zużywanej przez przepływający prąd. Korzystamy ze wzoru W = U * I * t, gdzie t oznacza czas, aby określić ilość pracy. Stąd wynika, że praca prądu zależy od napięcia, natężenia oraz czasu, przez jaki prąd płynie. Wynik wyrażamy w dżulach (J), co pozwala na ocenę zużycia energii elektrycznej.

Zrozumienie tych zależności jest niezbędne przy analizie i projektowaniu systemów elektrycznych. Ułatwia również rozwiązywanie problemów praktycznych związanych z przepływem prądu w różnych technologiach.